Нарисуйте куб закрасьте разными цветами пересечение – Нарисуйте куб.Укажите пересечение 1.нижней и правой грананей2передней и верхней граней 3..задней и левой граней .4.переднней,нижней и правой
23.11.2016 


 Советы художника
Советы художника
Как правильно нарисовать куб карандашом
Все предметы, которые нас окружают можно мысленно вписать в простые геометрические тела (куб, шар, конус, цилиндр, призма и др.). Изучая форму куба, мы узнаем, как нарисовать, к примеру, дом, потому что упрощенно дом рисуется с использованием тех же приемов что и куб. У него есть вершины, ребра и грани, как и у куба. Крыша дома – это многогранная призма.
Нарисуем куб с натуры, а затем будем использовать эти знания на наших курсы рисования в Киеве для изображения более сложных предметов таких как дома и улицы.
Куб – геометрическое тело, образованное пересечением плоскостей. И, как всякий объемный предмет, при изображении на плоском листе он будет претерпевать изменения в соответствии с законами перспективы. На рисунке изображена линия горизонта это уровень плоскости зрения художника. На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
Мы изображаем предметы в пространстве так, как их воспринимает наш глаз. (Чем дальше от зрителя, тем меньше выглядит предмет и т.д.)
Начало любой картины – это композиция. Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Рисуем самое ближнее вертикальное ребро кубаРасположите самое ближнее вертикальное ребро так, чтобы оно не совпадало с центром листа, проходящим через пересечение его диагоналей. Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
Изображение верхних ребер куба То же проделаем и с верхними ребрами. Как передавать пространство на листе нам объясняют основные законы линейной перспективы. Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше. Таким образом, все ребра будут разной высоты. Пересечение дальних горизонтальных ребер кубаПри пересечении дальних горизонтальных ребер образовались вершины. Через них проходит самое дальнее, невидимое глазом, ребро. На начальном этапе изобразим куб прозрачным для понимания полной конструкции предмета.
Для того, чтобы узнать на сколько сократились боковые грани, воспользуемся методом визирования. При помощи этого метода происходит восприятие очертаний предмета, художник учится изображать предметы пропорциональными и в различных ракурсах.
Как он работает? Возьмите карандаш на вытянутой руке, прикройте один глаз, совместите карандаш и изображение ребра куба в пространстве. Верхний край карандаша должен совпадать с верхней вершиной ребра, а пальцем зажмите на карандаше точку, совпадающую с нижней вершиной. Не убирая палец с карандаша, разверните под прямым углом и измеряйте расстояние между двумя ребрами. Таким образом, мы увидим соотношение высоты и ширины одной грани. Запомните это соотношение и передайте его на рисунке. Этим методом можно измерять и изображать так же соотношение ребер.
После того, как закончены линейные построения, приступаем к воздушной перспективе, а значит к штриховке.
Основная задача художника передавать объемные формы предметов. У нашего кубика мы видим три грани, все они разные по тону. Левая грань самая темная — это собственная тень предмета. Благодаря отраженному свету от окружающих предметов или рефлексам, штриховку делаем немного светлее по мере удаления влево. Самое большое ребро делают контрастней, чем все остальные. Таким образом, показывают его приближенность на передний план.
Воздушная перспектива и штриховка кубаВерхняя плоскость темнее, чем вертикальная справа. Свет по ней лишь скользит, образуя полутон. Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Для работы над самой светлой гранью возьмем твердый карандаш Н или 2Н. Он не даст сделать тон слишком темным. Штриховку нанесем вертикальную, по направлению плоскости.
Падающие тени и собственная тень кубаПадающие тени всегда темнее, чем собственная тень предмета. Ближнее ребро – это линия перехода света и тени. Из нее начинается падающая тень. Чем ближе к предмету, тем насыщеннее тон. Отраженный свет от куба создает рефлекс внутри тени и она немного высветляется.
Куб нарисованный по законам перспективного построения и воздушной перспективыРисование простых геометрических тел часто используется на курсы академического рисунка в Киеве и позволяет начинающему художнику научиться изображать предметы в пространстве, применяя законы перспективного построения и воздушной перспективы.
Поделиться ссылкой:
Похожее
artclass.kiev.ua
Занимательные задачи с кубиками
- Яковлева Татьяна Петровна, доцент кафедры математики и физики, ФГБОУ ВПО «Камчатский государственный университет им. Витуса Беринга», г. Петропавловск-Камчатский, Камчатский край
Разделы: Математика, Внеклассная работа
Умение решать задачи — такое же
практическое искусство, как умение плавать и
бегать. Ему можно научиться только путем
подражания и упражнения.
Д. Пойа
Задачи играют огромную роль в жизни человека. Задачи, которые ставит перед собой человек, и задачи, которые ставят перед ним другие люди и обстоятельства жизни, направляют всю его деятельность всю его жизнь. Известный русский методист В.А. Евтушевский так охарактеризовал функции задач в обучении: «Задачи, предлагаемые в классе, заключают в себе живой материал для упражнения мышления ученика, для вывода математических правил и для упражнения в приложении этих правил в решении частных практических вопросов» [16, с. 3].
Представленные занимательные задачи с кубиками разнообразны, так как можно выделить кубики, на гранях которых изображены цифры, буквы, рисунки, цветовая гамма. Такие задачи применимы для детей широкой возрастной категории на различных этапах урока математики, во внеклассной работе. Все они способствуют:
- обучению чтению графической информации, изображения геометрических объектов;
- развитию пространственного воображения;
- формированию умений мысленно представлять различные положения предмета и изменения его положения в зависимости от разных точек отсчета и умения зафиксировать это представление на изображении;
- обучению логическим обоснованиям геометрических фактов;
- развитию конструкторских способностей, моделированию;
- развитию познавательных процессов: восприятия, внимания, памяти, мышления;
- развитию исследовательских навыков.
Занимательные задачи с игральными кубиками привлекут внимание детей и сделают интерес к математике достаточно стойким, помогут овладеть математическими умениями не только сильным ученикам, но и тем, для которых данный школьный предмет является наиболее сложным.
Задачи.
Задача № 1. Занумеруйте 8 вершин кубика порядковыми числами (1, 2, 3, 4, 5, 6, 7, 8) так, чтобы сумма номеров на каждой из шести его граней оказалась одинаковой (рис. 1а).
Ответ. Каждая вершина кубика принадлежит трем граням, поэтому сумму 1 + 2 + : + 8 следует умножить на 3, затем разделить на 6 (на число граней), получится 18 — сумма номеров на каждой грани (рис. 1б).
Рисунок 1.
Задача № 2. Можно ли «занумеровать» все ребра целыми числами так, чтобы суммы номеров ребер, сходящихся в каждой вершине, были одинаковыми, если это числа: а) 1; 2; :; 12; б) -6; -5; :; -1; 1; 2; :; 6?
Ответ.
а) Нет. Предположим, что это возможно и сумма номеров ребер, сходящихся в каждой вершине, равна х. Тогда сумма чисел на всех восьми ребрах куба равна 8х. С другой стороны, так как каждый номер вошел в эту сумму дважды, то эта же сумма равна: (1 + 2 + : + 11 + 12) 2 = (1 + 12) 12 = 156. Уравнение 8х = 156 в целых числах решения не имеет, поэтому наше предположение неверно.
б) Да. Сумма номеров ребер, сходящихся в каждой вершине равна 0 (рис. 2).
Рисунок 2.
Задача № 3. На рис. 3 изображена фигура, являющаяся разверткой куба. Тонкие линии — это линии сгиба. Мысленно сверните куб из развертки. Определите, какая грань является верхней, если закрашенная грань — нижняя.
Рисунок 3.
Ответ. «в».
Задача № 4. На гранях непрозрачного кубика написаны буквы так, как показано на рис. 4а. Кубик подбросили, и он упал так, что одна из букв стала располагаться, как показано на рис. 4б. Нанесите на остальные грани кубика соответствующие буквы (они могут оказаться повернутыми). Проверьте свой ответ с помощью модели куба.
Рисунок 4.
Ответ. Рис. 4в.
Задача № 5. Мысленно сверните куб из каждой развертки данной на рис. 5 и определите, какая грань является верхней, если нижняя грань заштрихована.
Ответ. а) Г, б) Б, в) Д, г) В.
Рисунок 5.
Задача № 6. Все кубики на рис. 6а одинаковы. Перечертите развертку одного из кубиков (рис. 6б) и нанесите не нее недостающие буквы.
Рисунок 6.
Ответ. Рис. 6в.
Задача № 7. Подбросили кубик (рис. 7а) так, что он упал, как показано на рис. 7б заполните пустые видимые грани куба.
Ответ. Рис. 7в.
Рисунок 7.
Задача № 8. В нужном месте лицевой стороны развертки куба запишите в правильном расположении буквы Г и Р (рис. 8).
Рисунок 8.
Ответ. Рис. 9.
Рисунок 9.
Задача № 9. Рассматривая каркас куба сначала спереди (вид А), затем слева (вид В) и, наконец, сверху (вид С), прочитайте слово, образованное жирными линиями (рис. 10).
Ответ. 1) БОР, 2) ЕЛЬ, 3) БЕС.
Рисунок 10.
Задача № 10. На рис. 11 изображена фигура, являющаяся разверткой куба (тонкие линии — это линии сгиба). Какие точки совместятся с точкой А при склеивании развертки, изображенной на рисунке?
Рисунок 11.
Ответ. М, H.
Задача № 11. Правильно изобразив сдвинутые между собой три прямоугольные проекции кубиков с буквами, прочтите русскую народную мудрость (рис. 12а).
Ответ. Леность — мать пороков (рис. 12б).
Рисунок 12.
Задача № 12. Из картона склеен кубик, на гранях которого нанесены буквы. На рис. 13а дан один вариант развертки этого кубика с изображением букв на его гранях.
Рисунок 13.
Нанесите буквы на пустые грани другого варианта развертки этого кубика (рис. 13б-г).
Ответ. Рис. 14.
Рисунок 14.
Задача № 13. Если вы догадаетесь, как расположить буквы на кубиках (на передних гранях), то буквы на верхних гранях составят новое слово (рис. 15).
Ответ. KITTEN — MONKEY.
Рисунок 15.
Задача № 14. Из фигур, изображенных на рис. 16, выберите те, которые являются разверстками кубика. Выделите их цветом. Перерисуйте данные изображения, вырежьте их и проверьте свой выбор.
Рисунок 16.
Ответ. «а», «б», «г», «д», «е», «ж».
Задача № 15. Какой из кубиков, изображенных на рисунках 17б-з, можно склеить из разверстки (рис. 17а)?
Рисунок 17.
Ответ. «е».
Задача № 16. На рис. 18 вы видите три детских кубика. Все они повернуты к нам одним и тем же рисунком — елочкой. Укажите, какие картинки мы увидим на каждом из кубиков, взглянув на них сверху, учитывая развертку кубика.
Рисунок 18.
Ответ. а) мяч, б) лист, в) тучка.
Задача № 17. Укажите раскраску граней куба на развертке, изображенной на рис. 19а-б, если на рис. 19в-д куб представлен в трех различных положениях.
Рисунок 19.
Ответ. Рис. 20.
Рисунок 20.
Задача № 18. Грани кубика окрашены так, как показано на рис. 21. Кубик подбросили. Он упал так, что передней гранью стала прозрачная грань. Раскрасьте в соответствующие цвета остальные грани кубика (рис. 21). Рассмотрите всевозможные варианты. Сделайте необходимую развертку. Вырежьте ее и проверьте свой ответ.
Рисунок 21.
Ответ. Рис. 22.
Рисунок 22.
Задача № 19. Из разноцветных кубиков сложили игрушку (рис. 23а). Раскрасьте кубики, если красный находится между синим и желтым, а желтый расположен под зеленым.
Рисунок 23.
Ответ. Рис. 23б.
Задача № 20. Покрасьте максимальное количество вершин куба в красный цвет так, чтобы среди красных вершин нельзя было выбрать три, образующие равносторонний треугольник.
Ответ. Максимальное возможное количество красных вершин равно четырем. Докажем это.
Покрасить четыре вершины возможно. Например, можно покрасить четыре вершины одной грани. В этом случае красные вершины образуют квадрат и среди них нет трех, образующих равносторонний треугольник.
Докажем, что покрасить пять вершин куба, удовлетворяющих условию, невозможно. Покрасим четыре вершины куба в синий цвет, а оставшиеся - в зеленый (рис. 24). Заметим, что между любыми двумя вершинами одного цвета одинаковое расстояние. Пусть мы смогли перекрасить пять вершин в красный цвет. Тогда какие-то три из них были покрашены в один цвет. Следовательно, они и образуют равносторонний треугольник.
Рисунок 24.
Задача № 21. На гранях кубика изображены такие фигуры, как на рис. 25а. Кубик последовательно перекатывают с грани на грань, как показано на рис. 25б. Какие фигуры должны располагаться на верхней и правой боковой гранях последнего изображения кубика?
Рисунок 25.
Ответ. На верхней грани — круг, на правой боковой грани — квадрат.
Задача № 22. Белый куб, ребро которого равно 3 см, окрасили синей краской, а затем распилили на кубики с ребром, длиной 1 см. Сколько среди них имеют одну окрашенную грань, две окрашенные грани, три окрашенные грани? Есть ли куб с неокрашенными гранями?
Ответ. Имеют одну окрашенную грань — 6 кубиков, две окрашенные грани — 12 кубиков, три окрашенные грани — 8 кубиков, куб с неокрашенными гранями — 1 кубик.
Задача № 23. Два куба, противоположные грани которых окрашены в один цвет, соединили вместе разными способами. Некоторые грани кубов забыли раскрасить. Раскрасьте их в соответствующие цвета (рис. 26).
Рисунок 26.
Ответ. Рис. 27.
Рисунок 27.
Задача № 24. После того, как развертка будет сложена в кубик, какой из приведенных ниже кубик получится (рис. 28)? (Не обращайте внимания на расположение рисунков).
Ответ. «г».
Рисунок 28.
Задача № 25. Какой из кубиков склеен из данной развертки (рис. 29)?
Ответ. «А».
Рисунок 29.
Задача № 26. Найдите объединение трех частей куба, стоящих слева от знаков равенства (рис. 30а,б), и нарисуйте его справа от знаков равенства так, как показано на примере (рис. 31).
Рисунок 30.
Рисунок 31.
Ответ. Рис. 32.
Рисунок 32.
Задача № 27. Каждая из фигур, изображенных слева от знаков равенства (рис. 33), является объединением двух частей куба, получаемых при его разрезании плоскостью, проходящей через центр. Восстановите эти части, изобразив ответ в виде, аналогичном предыдущему заданию.
Рисунок 33.
Ответ. Рис. 34.
Рисунок 34.
Задача № 28. Все грани кубика окрашены в разные цвета, причем каждая грань окрашена одним цветом. Если на этот кубик смотреть с одной стороны, то видны голубая, желтая и белая грани. С другой стороны видны черная, голубая и красная грани. С третьей стороны видны зеленая, черная и белая грани. Какая грань расположена против белой?
Ответ. Против белой грани расположена красная грань.
Задача № 29. Сколько кубиков использовано для построения башни (рис. 35)?
Рисунок 35.
Ответ. а) 28; б) 44.
Задача № 30. Сколько кубиков нужно, чтобы сложить такую фигуру (рис. 36)?
Ответ. 106 кубиков.
Рисунок 36.
Задача № 31. На рис. 37а изображены четыре куба. Они окрашены по-разному, но при этом у каждого из них противоположные грани имеют одинаковый цвет. Из этих кубиков построили фигуры «пьедестал» и потом параллелепипед. Строили так, чтобы соприкасающиеся грани кубиков были одинакового цвета. Закончите раскраску фигур на рис. 37б,в и укажите номера кубиков.
Рисунок 37.
Ответ. Рис. 38.
Рисунок 38.
Задача № 32. Путешествие мухи. Муха, отправляясь из точки А, может обойти четыре стороны основания куба за 4 мин. За какое время она доберется из А в противоположную вершину В (рис. 39а).
Рисунок 39.
Ответ. Умная муха избрала бы путь, отмеченный на рис. 39б сплошной линией, на его преодоление уйдет 2,236 мин. Путь, отмеченный пунктирной линией, длиннее, и на него уйдет больше времени.
Задача № 33. Большой кубик склеен из маленьких деревянных кубиков. В нем просверлили 6 сквозных отверстий, параллельных ребрам (рис. 40). Сколько маленьких кубиков осталось не поврежденными?
Рисунок 40.
Ответ. 44 кубика.
Задача № 34. У меня есть кусок сыра в форме куба. Как мне следует провести один прямой разрез ножом, чтобы две новые грани оказались правильными шестиугольниками? Разумеется, если мы разрежем сыр в направлении пунктирной линии на рис. 41а, то получим два квадрата. Попробуйте получить шестиугольники.
Ответ. Отметьте середины ребер BC, CH, HE, EF, FG и GB. Затем, начиная сверху, проведите разрез вдоль плоскости, обозначенной пунктирной линией (рис. 41б). Тогда каждая из двух новых поверхностей окажется правильным шестиугольником, а правый кусок будет выглядеть примерно так, как показано на рис. 41в.
Рисунок 41.
Задача № 35. Рекламное агентство направило эти рисунки заказчику — производителю упаковки. Ему предложили решить, какой цвет должен быть на той стороне упаковки, которая находится напротив желтой стороны на рис. 42 В. На следующий день заказчик позвонил. Какой вопрос он задал?
Рисунок 42.
Ответ. Он спросил: «Здесь ошибка или вы намеренно повторили желтый цвет?» Полная схема изображена на рис. 43.
Рисунок 43.
Задача № 36. На этих архитектурных макетах каждый куб является отдельной квартирой (рис. 44). Контракт на строительство достанется тому архитектору, на макете которого больше квартир. Какой из макетов отвечает этому требованию?
Рисунок 44.
Ответ. Этому требованию отвечает макет здания А; в этом здании 80 квартир, а в здании Б — всего 79.
Задача № 37. Стала классической легенда, связанная с задачей об удвоении поверхности куба. Филопон рассказывает, как афиняне, напуганные эпидемией чумы 432 г. до н. э., обратились за советом к Платону. Но прежде чем прийти к великому философу, они воззвали к Аполлону, который устами Дельфийского оракула повелел им вдвое увеличить размеры золотого алтаря в своем храме. Однако афиняне оказались неспособными это сделать. Платон сказал, что несчастье постигло их из-за злостного пренебрежения возвышенной наукой геометрией, и посетовал, что среди них не нашлось ни одного человека, достаточно мудрого, чтобы решить эту задачу.
Задача Дельфийского оракула, где речь идет просто об удвоении куба, так тесно связана с задачей о кубах Платона, что не слишком искушенные в математике авторы их часто путают. Последнюю задачу называют также задачей о геометрических числах Платона, утверждая обычно, что об истинных ее условиях почти ничего не известно. Некоторые считают, даже, что ее условия утеряны.
Существует древнее описание массивного куба, воздвигнутого в центре выложенной плитами площадки, и не требуется большого воображения, чтобы связать этот монумент с задачей Платона. На рисунке 45 вы видите Платона, созерцающего такой массивный мраморный куб, который сложен из некоторого числа меньших кубов. Монумент возвышается в центре квадратной площадки, выложенной такими же малыми мраморными кубами.
Рисунок 45.
Число кубов в площадке и в монументе одинаково. Скажите, сколько кубов требуется, чтобы построить монумент и квадратную площадку, и вы решите великую задачу о геометрических числах Платона.
Ответ. В задаче нужно найти число, которое, будучи возведенным в куб, даст точный квадрат. Так происходит, оказывается, с любым числом, которое само является квадратом. Наименьший квадрат (если не считать 1) равен 4, так что монумент мог содержать 64 малых куба (4 * 4 * 4) и стоять в центре квадрата 8 * 8. Конечно, это не согласуется с пропорциями, приведенными на рисунке. Поэтому мы испробуем следующий квадрат, 9, что приводит к монументу из 729 кубов, стоящему на квадрате 27 * 27. Это и есть правильный ответ, ибо только он согласуется с рисунком.
Задача № 38. На Востоке искусство смешивания различных сортов чая не пренебрегает миллионными долями унции! Говорят, секреты некоторых смесей сохранялись в глубокой тайне и веками их не удавалось повторить.
Дабы проиллюстрировать, сколь сложно проникнуть в тайну искусства смешивания чая, мы предлагаем вашему вниманию одну простую задачу, где смешиваются только два сорта.
Составитель смесей получил два ящика чая. Оба они были кубической формы, но имели разные размеры. В большем ящике находился черный чай, а в меньшем — зеленый. Смешав содержимое этих ящиков, человек обнаружил, что полученной смесью удалось заполнить ровно 22 коробки кубической формы и одинакового размера. Допустим, что внутренние размеры коробок выражаются конечной десятичной дробью. Сумеете ли вы определить, в какой пропорции в данную смесь входили черный и зеленый чай? Другими словами, найдите два различных рациональных числа, таких, чтобы при сложении их кубов получился результат, который после деления на 22 и последующего извлечения кубического корня привел бы тоже к рациональному числу.
Ответ. У куба с ребром в 17, 299 дюйма и у куба с ребром в 25,469 дюйма суммарный объем (21697,794418608 кубического дюйма) в точности равен суммарному объему 22 кубов с ребром в 9, 954 дюйма каждый. Следовательно, зеленый и черный чай были смешаны в пропорции (17299)3 к (25469)3.
Список литературы:
- Бизам Д., Герцег Я. Игра и логика. 85 логических задач / пер. с венг. Ю.А. Данилова. — М.: Мир, 1975. — 358 с.
- Внеклассная работа по математике в 4-5 классах / под ред. С.И. Шварцбурда. — М.: Просвещение, 1974. — 191 с.
- Внеклассная работа по математике в 6-8 классах / под ред. С.И. Шварцбурда. — М.: Просвещение, 1977. — 288 с.
- Гарднер М. А ну-ка, догадайся! / пер. с англ. — М.: Мир, 1984. — 213 с.
- Гарднер М. Математические чудеса и тайны: пер. с англ. / под ред. Г.Е. Шилова. — 5-е изд. — М.: Наука, 1986. — 128 с.
- Гарднер М. Математические досуги: пер. с англ. / под ред. Я.А. Смородинского. — М.: Мир, 1972. — 496 с.
- Гарднер М. Математические новеллы: пер. с англ. / под ред. Я.А. Смородинского. — М.: Мир, 1974. — 456 с.
- Глеман М., Варга Т. Вероятность в играх и развлечениях: элементы теории вероятностей в курсе сред. Школы: пособие для учителя / пер. с фр. А.К. Звонкина. — М.: Просвещение, 1979. — 176 с.
- Занимательная математика. 5-11 классы. (Как сделать уроки математики нескучными) / авт.-сост. Т.Д. Гаврилова. — Волгоград: Учитель, 2005. — 96 с.
- Кордемский Б.А. Математические завлекалки. — М.: Издательский Дом ОНИКС: Альянс-В, 2000. — 512 с.
- Математика: Интеллектуальные марафоны, турниры, бои: 5-11 классы. Книга для учителя. — М.: Издательство «Первое сентября», 2003. — 256 с.
- Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями /пер. с англ. — М.: Наука, 1985. — 88 с.
- Олимпиадные задачи по математике. 5-8 классы. 500 нестандартных задач для проведения конкурсов и олимпиад: развитие творческой сущности учащихся / авт.-сост. Н.В. Зоболотнева. — Волгоград: Учитель, 2005. — 99 с.
- Перельман Я.И. Занимательные задачи и опыты. - М.: Детская литература, 1972. — 464 с.
- Рассел К., Картер Ф. Тренинг интеллекта. — М.: Эксмо, 2003. — 96 с.
- Фридман Л.М. Сюжетные задачи по математике. История, теория, методика. — М.: Школьная пресса, 2002. — 208 с.
- Шарыгин И.Ф., Шевкин А.В. Математика: задачи на смекалку: учеб. пособие для 5-6 кл. общеобразоват. учреждений. — М.: Просвещение, 1995. — 80 с.
28.11.2010
xn--i1abbnckbmcl9fb.xn--p1ai
Академический рисунок куба. Основные правила поэтапного рисования

Изображение куба – самое простое и первое задание по изображению предметов в пространстве. Для этого вам уже нужно знать правила передачи тонов, а также воздушной и линейной перспективы. Пропускать это академический рисунок куба нельзя, ведь именно на нём закладываются основы передачи объема и пространства. Уже на этом задании многие ученики делают массу ошибок, если их вовремя не исправить, то они переползут на будущие работы.
Общие правила рисования
Напоминаем, что задача изображения куба – тренировка умения видеть пропорции, оттенки и отображать их на листе бумаги. Поэтому при рисовании следуйте нескольким правилам, без них вы не приобретете нужного навыка.
 Реальный предмет. При рисовании вам потребуется реальный куб белого цвета. В художественной школе вам дадут гипсовое изделие. В домашних условиях натуру можно сделать из куска картона или бумаги. Сторона одной грани должна быть 10-15 см, поэтому понадобится несколько листов бумаги. Под изготовленный куб также положите белую или серую скатерть, чтобы тень от предмета была четко видна.
Реальный предмет. При рисовании вам потребуется реальный куб белого цвета. В художественной школе вам дадут гипсовое изделие. В домашних условиях натуру можно сделать из куска картона или бумаги. Сторона одной грани должна быть 10-15 см, поэтому понадобится несколько листов бумаги. Под изготовленный куб также положите белую или серую скатерть, чтобы тень от предмета была четко видна.
 Положение куба. Источник света должен находиться сверху и сбоку, чтобы свет освещал две видимые грани. Сам куб должен располагаться прямо перед вами и немного снизу, чтобы видны были три его грани. В идеале нужен натуральный свет, но сгодиться и свет от лампы. Разумеется, при рисовании нужно сидеть ровно, чтобы угол зрения не изменялся.
Положение куба. Источник света должен находиться сверху и сбоку, чтобы свет освещал две видимые грани. Сам куб должен располагаться прямо перед вами и немного снизу, чтобы видны были три его грани. В идеале нужен натуральный свет, но сгодиться и свет от лампы. Разумеется, при рисовании нужно сидеть ровно, чтобы угол зрения не изменялся.
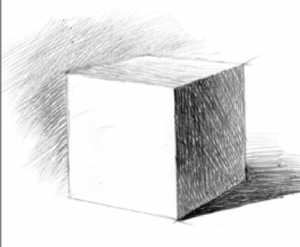 Оптимальное расстояние от глаз до куба в 2-3 раза больше размеров изображаемого пространства. Обратите внимание, что учитывать нужно полностью все изображаемое пространство вместе со скатертью, а не только куб. В итоге расстояние до куба должно составить около 50-70 см.
Оптимальное расстояние от глаз до куба в 2-3 раза больше размеров изображаемого пространства. Обратите внимание, что учитывать нужно полностью все изображаемое пространство вместе со скатертью, а не только куб. В итоге расстояние до куба должно составить около 50-70 см.
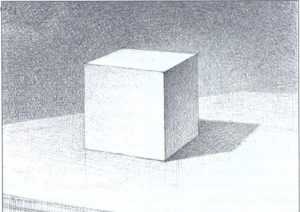 Рисовать нужно пространство целиком. Ведь вы планируете рисовать картины с сюжетом, а не просто отдельные предметы на холсте. Поэтому привыкайте к отображению целой видимой картины, а не отдельных элементов на ней. К тому же важной частью задания будет отображение тени от куба на скатерти.
Рисовать нужно пространство целиком. Ведь вы планируете рисовать картины с сюжетом, а не просто отдельные предметы на холсте. Поэтому привыкайте к отображению целой видимой картины, а не отдельных элементов на ней. К тому же важной частью задания будет отображение тени от куба на скатерти.
 Границы и перспектива в академическом рисунке
Границы и перспектива в академическом рисунке
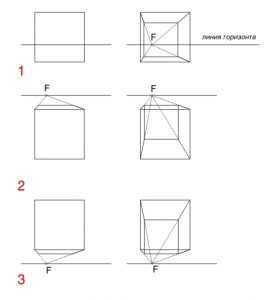
Сначала легкими линиями изображаем положение куба на листе бумаги. Предмет вместе с тенью должен находиться по центру листа. Сначала изображаем тонкими линиями грани куба, они у него параллельны. Но по законам отображения объема все параллельные линии в перспективе соединяются в одной точке на горизонте. Кажется, что для такого небольшого размера как куб это правило не важно, но оно обязательно для выполнения.
 По законам линейной перспективы мы должны изобразить 8 ребер, половина из которых направлена влево, а другая – вправо. Вопрос лишь в том, в какой точке пространства линии от ребер куба должны соединиться? Все параллельные линии сходятся в точку на горизонте, а он расположен на уровне глаз художника. Представьте, что за кубом нет стены, и вы видите схождение неба и земли, мысленно проведите линии границ ребер до горизонта.
По законам линейной перспективы мы должны изобразить 8 ребер, половина из которых направлена влево, а другая – вправо. Вопрос лишь в том, в какой точке пространства линии от ребер куба должны соединиться? Все параллельные линии сходятся в точку на горизонте, а он расположен на уровне глаз художника. Представьте, что за кубом нет стены, и вы видите схождение неба и земли, мысленно проведите линии границ ребер до горизонта.
 Так как мы смотрим на куб несколько сверху, то в перспективе вертикальные линии тоже могут соединяться. Однако в академическом рисунке куба это не предусматривается, поэтому вертикальные линии можно рисовать параллельно. Также обратите внимание на то, что чем больше грань куба на рисунке повернута к зрителю, тем меньше сокращается расстояние в перспективе между гранями.
Так как мы смотрим на куб несколько сверху, то в перспективе вертикальные линии тоже могут соединяться. Однако в академическом рисунке куба это не предусматривается, поэтому вертикальные линии можно рисовать параллельно. Также обратите внимание на то, что чем больше грань куба на рисунке повернута к зрителю, тем меньше сокращается расстояние в перспективе между гранями.
Штриховка и объем
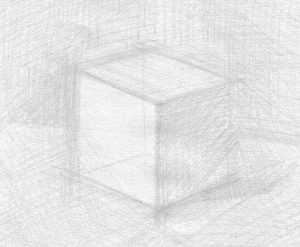 Приступая к объему, выделите ближайшие грани более жирно. Можно заметить, что от одного лишь жирного выделения грани стали смотреться «ближе». Это ярко демонстрирует один из важнейших принципов передачи пространства – при удалении от зрителя краски теряют контрастность. Поэтому передние края плоскостей куба лучше сделать более контрастными.
Приступая к объему, выделите ближайшие грани более жирно. Можно заметить, что от одного лишь жирного выделения грани стали смотреться «ближе». Это ярко демонстрирует один из важнейших принципов передачи пространства – при удалении от зрителя краски теряют контрастность. Поэтому передние края плоскостей куба лучше сделать более контрастными.
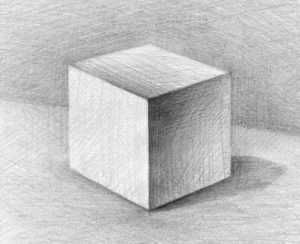 Тон лучше набирать постепенно, сначала твердым карандашом, постепенно добавляя штрихи мягким грифелем. Чтобы не ошибиться с тоном, создавайте светотень сразу на всем рисунке. Тогда ошибку в передачи тени, света и тонов можно будет увидеть на ранней стадии. При штриховке левой грани лучше использовать вертикальные штрихи. Для штриховки верхней и правой грани подойдут диагональные штрихи. В заключении добавьте больше контраста на передний край куба.
Тон лучше набирать постепенно, сначала твердым карандашом, постепенно добавляя штрихи мягким грифелем. Чтобы не ошибиться с тоном, создавайте светотень сразу на всем рисунке. Тогда ошибку в передачи тени, света и тонов можно будет увидеть на ранней стадии. При штриховке левой грани лучше использовать вертикальные штрихи. Для штриховки верхней и правой грани подойдут диагональные штрихи. В заключении добавьте больше контраста на передний край куба.
art-matita.ru
|
gavrilovart.ru
Гиперкуб
ГиперкубЕщё когда я был студентом-первокурсником у меня с одним моим одногруппником вышел горячий спор. Он говорил, что четырёхмерный куб представить нельзя ни в каком виде, а я уверял, что его можно представить достаточно отчётливо. Тогда я даже сделал из скрепок проекцию гиперкуба на наше трёхмерное пространство… Но давайте обо всём по-порядку.
Что такое гиперкуб и четырёхмерное пространство
В нашем привычном пространстве три измерения. С геометрической точки зрения это значит, что в нём можно указать три взаимно-перпендикулярных прямых. То есть для любой прямой можно найти вторую, перпендикулярную первой, а для пары можно найти третью прямую, перпендикулярную двум первым. Найти четвёртую прямую, перпендикулярную трём имеющимся, уже не удастся.
Четырёхмерное пространство отличается от нашего только тем, что в нём есть ещё одно дополнительное направление. Если у вас уже есть три взаимно перпендикулярные прямые, то вы можете найти четвёртую, такую, что она будет перпендикуляра всем трём.
Гиперкуб это просто куб в четырёхмерном пространстве.
Можно ли представить четырёхмерное пространство и гиперкуб?
Этот вопрос сродни вопросу: «можно ли представить Тайную Вечерю, посмотрев на одноимённую картину (1495-1498) Леонардо да Винчи (1452-1519)?»
С одной стороны, вы конечно не представите то, что видел Иисус (он сидит лицом к зрителю), тем более вы не почувствуете запаха сада за окном и вкуса еды на столе, не услышите пения птиц… Вы не получите полного представления о происходившем в тот вечер, но нельзя сказать, что вы не узнаете ничего нового и что картина не представляет никакого интереса.
Аналогичная ситуация и с вопросом о гиперкубе. Полностью представить его нельзя, но можно приблизиться к пониманию, каков он.
Построение гиперкуба
0-мерный куб
Начнём с начала — с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.
1-мерный куб
В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.
Это одномерный куб.
2-мерный куб
У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.
Это куб в двумерном пространстве.
3-мерный куб
С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.
4-мерный куб (гиперкуб)
Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.
Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции. О проекциях мы поговорим чуть позже, а пока немного голых фактов и цифр.
Количество вершин, рёбер, граней
| Характеристики кубов различной размерности | |||
|---|---|---|---|
| размерность пространства | количество вершин | количество рёбер | количество граней |
| 0 (точка) | 1 | 0 | 0 |
| 1 (отрезок) | 2 | 1 | 2 (точки) |
| 2 (квадрат) | 4 | 4 | 4 (отрезки) |
| 3 (куб) | 8 | 12 | 6 (квадраты) |
| 4 (гиперкуб) | 16 | 32 | 8 (кубы) |
| N (общая формула) | 2N | N·2N-1 | 2·N |
Обратите внимание, что гранью гиперкуба является наш обычный трёхмерный куб. Если внимательно посмотреть на рисунок гиперкуба, то можно действительно найти восемь кубов.
Проекции и зрение жителя четырёхмерного пространства
Несколько слов о зрении
Мы живём в трёхмерном мире, но видим мы его двумерным. Это связано с тем, что сетчатка наших глаз расположена в плоскости, имеющей только два измерения. Именно поэтому мы способны воспринимать двумерные картины и находить их похожими на реальность. (Конечно, благодаря аккомодации, глаз может оценить расстояние до объекта, но это уже побочное явление, связанное с оптикой, встроенной в наш глаз.)
Глаза жителя четырёхмерного пространства должны иметь трёхмерную сетчатку. Такое существо может сразу увидеть трёхмерную фигуру полностью: все её грани и внутренности. (Точно так же мы можем увидеть двумерную фигуру, все её грани и внутренности.)
Таким образом, с помощью наших органов зрения, мы не способны воспринять четырёхмерный куб так, как его воспринимал бы житель четырёхмерного пространства. Увы. Остаётся только уповать на мысленный взор и фантазию, которые, к счастью, не имеют физических ограничений.
Тем не менее, изображая гиперкуб на плоскости, я просто вынужден делать его проекцию на двумерное пространство. Учитывайте это обстоятельство, при изучении рисунков.
Пересечения рёбер
Естественно, ребра гиперкуба не пересекаются. Пересечения появляются только на рисунках. Впрочем, это не должно вызывать удивления, ведь рёбра обычного куба на рисунках тоже пересекаются.
Длины рёбер
Стоит отметить, что все грани и рёбра четырёхмерного куба равны. На рисунке они получаются не равными только потому, что расположены под разными углами к направлению взгляда. Однако можно развернуть гиперкуб так, что все проекции будут иметь одинаковую длину.
Кстати, на этом рисунке отчётливо видны восемь кубов, являющихся гранями гиперкуба.
Гиперкуб внутри пустой
В это трудно поверить, но между кубами, ограничивающими гиперкуб, заключено некоторое пространство (фрагмент четырёхмерного пространства).
Чтобы это лучше понять, давайте рассмотрим двумерную проекцию обычного трёхмерного куба (я специально сделал её несколько схематичной).
Можно ли по ней догадаться, что внутри куба есть некоторое пространство? Да, но только применив воображение. Глаз этого пространства не видит. Это происходит потому, что рёбра, расположенные в третьем измерении (которое нельзя изобразить на плоском рисунке), теперь превратились в отрезки, лежащие в плоскости рисунка. Они больше не обеспечивают объём.
Квадраты, ограничивающие пространство куба, наложились друг на друга. Но можно представить, что в исходной фигуре (трёхмерном кубе) эти квадраты располагались в разных плоскостях, а не один поверх другого в одной плоскости, как это получилось на рисунке.
Точно так же дело обстоит и с гиперкубом. Кубы-грани гиперкуба на самом деле не накладываются, как это кажется нам на проекции, а располагаются в четырёхмерном пространстве.
Развёртки
Итак, житель четырёхмерного пространства может увидеть трёхмерный объект одновременно со всех сторон. Можем ли мы одновременно со всех сторон увидеть трёхмерный куб? Глазом — нет. Но люди придумали способ, как изобразить на плоском рисунке все грани трёхмерного куба одновременно. Такое изображение называется развёрткой.
Развёртка трёхмерного куба
Как образуется развёртка трёхмерного куба все наверно знают. Этот процесс показан на анимации.
Для наглядности края граней куба сделаны полупрозрачными.
Следует отметить, что мы способны воспринять эту двумерную картинку только благодаря воображению. Если рассмотреть фазы разворачивания с чисто двумерной точки зрения, то процесс будет казаться странным и совсем не наглядным.
Он выглядит, как постепенное появление сперва очертаний искажённых квадратов, а потом их расползание на свои места с одновременным принятием необходимой формы.
Если смотреть на разворачивающийся куб в направлении одной из его граней (с этой точки зрения куб выглядит как квадрат), то процесс образования развёртки ещё менее нагляден. Всё выглядит как выползание квадратов из начального квадрата (не развёрнутого куба).
Но не наглядна развёртка только для глаз. Как раз благодаря воображению из неё можно почерпнуть много информации.
Развёртка четырёхмерного куба
Сделать анимированный процесс разворачивания гиперкуба хоть сколько нибудь наглядным просто невозможно. Но этот процесс можно представить. (Для этого надо посмотреть на него глазами четырёхмерного существа.)
Развёртка выглядит так.
Здесь видны все восемь кубов, ограничивающих гиперкуб.
Одинаковыми цветами покрашены грани, которые должны совместиться при сворачивании. Серыми оставлены грани для которых парных не видно. После свёртки самая верхняя грань верхнего куба должна совместиться с нижней гранью нижнего куба. (Аналогично сворачивается развёртка трёхмерного куба.)
Обратите внимание, что после свёртки все грани восьми кубиков придут в соприкосновение, замкнув гиперкуб. И наконец, представляя процесс свёртывания, не забывайте, что при свёртывании происходит не наложение кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области.
Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты фигурируют в очень многих его картинах. На картине «Распятие» (1954) используется развёртка гиперкуба.
Пространство-время и евклидово четырёхмерное пространство
Надеюсь, что вам удалось представить гиперкуб. Но удалось ли вам приблизиться к пониманию, как устроено четырёхмерное пространство-время в котором мы живём? Увы, не совсем.
Здесь мы говорили об евклидовом четырёхмерном пространстве, но пространство-время обладает совсем другими свойствами. В частности, при любых поворотах отрезки остаются всегда наклонены к оси времени либо под углом меньше 45 градусов, либо под углом больше 45 градусов.
Свойствам пространства времени я посвятил серию заметок.
Отправить
www.michurin.net
Рисуем куб
Рисование куба — главный этап освоения академического рисунка. Из различных геометрических фигур куб считается простым для начинающих. На примере изображения различных форм куба, люди обучаются правилам линейной и воздушной перспективы, правильной штриховке, а также усваивают передачу объемной формы предметов.
Для рисования необходим графический планшет. Если его нет — карандаш и лист бумаги. Мышка тут никак не подойдет. Также понадобится белый гипсовый куб, так как на белом лучше видна его светотень. Вместо гипсового куба можно использовать пластиковывй или бумажный. Но наличие натуры обязательно, так обучаться гораздо удобней.
Как нарисовать куб
Куб — это прямоугольная призма, у которой стороны равны, и есть 6 граней. Противоположенные грани параллельны. Ребрами куба называют места пересечения граней. Ребра делятся на три группы, в каждой из которых абсолютно все грани параллельны.
Набросок
Для начала рисования наметим место, где будет располагаться куб, едва заметными линиями. Само изображение мы будем располагать немного выше середины холста, оно не должно быть слишком крупным или слишком мелким.
Теперь проведем ближнюю к нам вертикальную линию — это основная линия при построении куба. Засечками сверху и снизу слегка ограничим высоту линии. Так как линия основная, необходимо предельно точно проследить, чтобы высота этого ребра была правильной по размеру. Это очень важно.
Основание куба
При рисовании основания куба очень важно определить углы наклона основных видимых граней, относительно основания. Это можно сделать очень простым способом: необходимо поднести карандаш на расстоянии вытянутой руки в строго горизонтальном положении к нижнему ближнему углу и запомнить углы, но не пытайтесь просто переносить углы на холст с помощью карандаша, это неправильно. Пытайтесь запомнить их и повторять. Только так будет «набиваться» рука и глазомер.
Далее необходимо учесть, что если грань куба больше развернута к вам, то угол меньше. Так можно определить какая грань меньше развернута, а какая — больше.
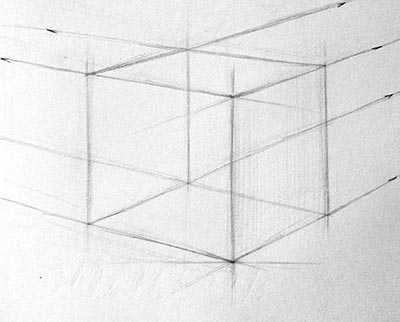
Можете нарисовать нижние грани, но до того, как перейти к началу рисования верхних, необходимо подумать над основным законом перспективы, который гласит, что любые параллельные линии, уходящие от зрителя, сокращаются в одну точку — точку схода.
У нашего куба имеется четыре ребра, которые смотрят направо и столько же ребер налево. Все четыре линии ребер, которые уходят влево, при их продолжении, сокращаются в одной точке схода слева, а все линии, которые уходят вправо — сходятся справа.
Но как правильно определить где все эти точки будут сходиться? Куб расположен на горизонтальной плоскости, а она параллельна поверхности земли как пол, стул и стол. И если наши линии удаляется от какого-либо предмета, то точка схода должна лежать именно на линии горизонта.
Но где же располагается линия горизонта? Всё просто: она всегда расположена на уровне глаз человека. Куда бы вы не смотрели — линия горизонта будет ровно на уровне ваших глаз. Проведите небольшое исследование: посмотрите в окно и представьте, где сходится земля с небом. Ответ будет очевиден. Даже если мы присядем, то и линия горизонта опустится.
Линию горизонта и точки схода рисуют тонкими линиями на листе до того, как нарисовать верхние грани.
Вертикальные линии и невидимые грани
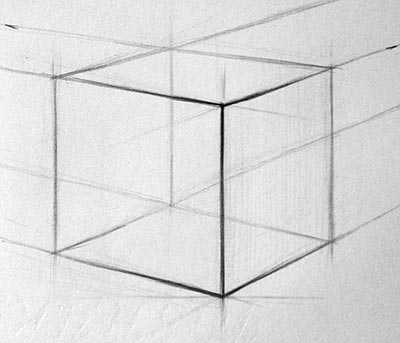
Обратите внимание на снимок куба в самом начале статьи. На нем отчетливо видно, что линии, которые расположены вертикально, немного наклонены. Это, прежде всего, связано с тем, что объектив фотокамеры, с которой производился снимок, увидел перспективное сокращение линий.
И это правда, когда мы видим куб сбоку и сверху, кажется что вертикальные линии чуть-чуть сходятся в одну точку которая располагается снизу. Академический рисунок игнорирует передачу сокращения вертикальных линий, за исключением случаев сильного ракурса, а при начальном уровне обучения, куб рисуется с параллельными вертикальными линиями, строго перпендикулярными линии горизонта.
Как только нарисованы верхние линии, проверяем, насколько сократились боковые грани с обеих сторон. Ширину данных граней меряем только по горизонтали, ни в коем случае не под наклоном, и переходим к сравниванию, какая из них меньше высоты самого ближнего бедра куба, и обязательно без между собой. Как только закончите с проверкой ближних линий и вертикальных ребер можете приступать к зарисовке дальних уходящих линий.
Невидимые линии также обязательно следует рисовать. Перед тем, как будете рисовать самое дальнее вертикальное бедро, убедитесь, что их точки схода расположены правильно. Если они расходятся и это заметно, то необходимо еще раз все тщательно проверить и исправить рисунок, самое главное не испортить его. Если расхождение линий не такое большое, необходимо просто немного подкорректировать линии и нарисовать дальше бедро, которое будет располагаться вертикально.
Как только, вы закончили с построением, выделите ближние к себе линии. Если линия темная — будет казаться, что она ближе. Зная это, можно передать пространство и объем.
Выделение ближних линий и штриховка
Главная задача штриховки — передать объем предметов. К штриховке нельзя приступать, если рисунок выполнен неправильно. Лучше начать заново или попытаться исправить текущий.
На кубе мы можем увидеть всего три плоскости — это верхняя и две боковые грани. Визуально каждая из граней уходит от смотрящего в пространство. Для того, чтобы показать форму, необходимо штриховать грани куба так, чтобы смотрящему было очевидно, что они действительно отдаляются.
Для того чтобы передать пространство применяются законы воздушной перспективы. Темные цвета светлеют в дали, а светлые — наоборот темнеют.
Может показаться, что куб настолько мал, что влияние воздушной перспективы незаметно, но мы должны рисовать руководствуясь законами, только соблюдая их куб станет объемным.
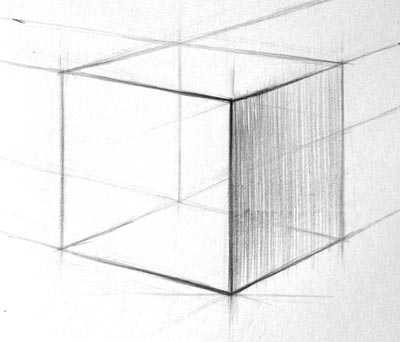
Сама штриховка начинаем строго с теневой части. У нашего куба грань справа в тени, поэтому начнем именно с нее. Штрихуем от себя. По мере удаления плоскости в пространстве нажим на карандаш слабее, это делает штрих светлее. Штриховка может быть как вертикальной, так и горизонтальной.
Осветленную левую часть штрихуем от себя, при этом левый угол оставляем белым, но слегка штрихуем дальнюю часть.
Верхнюю поверхность делаем как полутон (промежуточное состояние между тенью и светом). Теперь оценим ее, задаваясь вопросом: «Она скорее светлая или темная?»
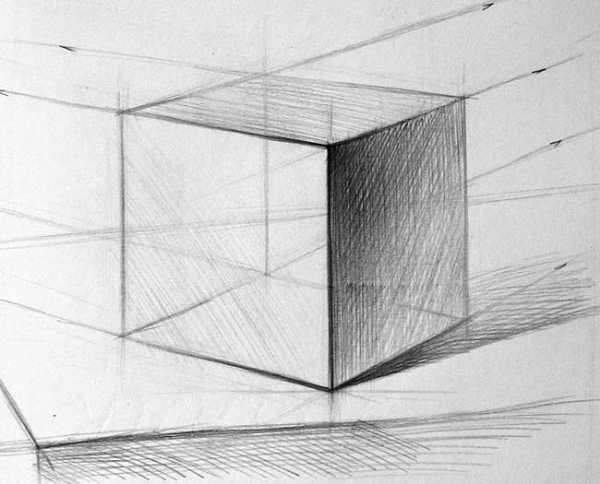
Всегда можно усилить тень, введя еще штрих, направленный строго по диагонали, также необходимо его растягивать — от темного к светлому. Подчеркиваем форму, делая тональные акценты, для этого можно использовать штриховку в разные стороны.
Не стоит забывать про тень от куба, которая расположена на плоскости, на которой он находится. Падающая тень на порядок темнее тени собственной. Плюс она граничит с рефлексом от освещенной плоскости (рефлекс — свет или цвет, отраженный от соседних поверхностей. Рефлекс тем светлее, чем источник отражающего света ярче и гораздо ближе).
Зеленый, красный и серый рефлексы на белом шаре.
Рисование других геометрических тел
Как только, вы почувствуете, что овладели навыками рисования куба — можно переходить на следующий уровень и рисовать другие геометрические фигуры. Полезнее всего рисовать их не в «одиночку» а группой. Для начала число геометрических фигур берите небольшое, примерно 2–3 фигуры.
При всем этом не забывайте, что фигуры нужно не просто копировать, а рисовать с учетом всех правил построения.
www.progimp.ru
Как нарисовать куб поэтапно | Хорошие уроки
Это средний по сложности урок. Повторить этот урок может быть затруднительно и взрослым, поэтому не рекомендую рисовать куб по этому уроку маленьким детям, но если есть большое желание — то можно и попробовать. Также хочу отметить урок «Как нарисовать паука» — обязательно попробуйте повторить его, если у вас останется время и желание рисовать сегодня.
Что понадобится
Для того, чтобы нарисовать куб нам может понадобиться:
- Бумага. Лучше брать среднезернистую специальную бумагу: начинающим художникам будет гораздо приятней рисовать именно на такой.
- Наточенные карандаши. Советую брать несколько степеней твердости, каждую нужно использовать для разных целей.
- Ластик.
- Палочка для растирания штриховки. Можно использовать обычную бумагу, скрученную в конус. Ей лего будет растирать штриховку, превращая её в монотонный цвет.
- Немного терпения.
- Хорошее настроение.
Поэтапный урок
Может показаться, что простые геометрические фигуры рисовать очень легко, но это ошибочная точка зрения. Чтобы правильно нарисовать куб нужно очень сильно постараться. Я рекомендую рисовать с натуры. Именно так вы сможете посмотреть куда именно падает свет, как и где он фигура отбрасывает тень. Фотография в этом случае не лучший помошник…
Кстати, кроме этого урока советую обратить своё внимание на урок «Рисуем санту». Он поможет повысить ваше мастерсово или просто доставит немного удовольствия.
Обратите внимание, что каждый предмет, каждое живое существо, каждое явление на бумаге можно изобразить при помощи простых геометрических предметов: кружочков, квадратиков и трегольников. Именно они создают форму, именно их нужно видеть художник в окружающих предметах. Нет дома, есть несколько больших прямоугольников и треугольник. Так строить сложные предметы гораздо легче.
Совет: создавайте набросок как можно менее толстыми штрихами. Чем толще будут штрихи наброска — тем трудней их будет стереть в последствии.
Первым шагом, точнее нулевым, всегда нужно размечать лист бумаги. Это даст вам понять где конкретно будет находиться рисунок. Если вы расположите рисунок на половине листа — вторую половину вы сможете использовать для другого рисунка. Вот пример разметки листа по центру:

Рисование куба — главный этап освоения академического рисунка. Из различных геометрических фигур куб считается простым для начинающих. На примере изображения различных форм куба, люди обучаются правилам линейной и воздушной перспективы, правильной штриховке, а также усваивают передачу объемной формы предметов.
Для рисования необходим графический планшет. Если его нет — карандаш и лист бумаги. Мышка тут никак не подойдет. Также понадобится белый гипсовый куб, так как на белом лучше видна его светотень. Вместо гипсового куба можно использовать пластиковывй или бумажный. Но наличие натуры обязательно, так обучаться гораздо удобней.Как нарисовать куб

Куб — это прямоугольная призма, у которой стороны равны, и есть 6 граней. Противоположенные грани параллельны. Ребрами куба называют места пересечения граней. Ребра делятся на три группы, в каждой из которых абсолютно все грани параллельны.
Набросок
Для начала рисования наметим место, где будет располагаться куб, едва заметными линиями. Само изображение мы будем располагать немного выше середины холста, оно не должно быть слишком крупным или слишком мелким.
Теперь проведем ближнюю к нам вертикальную линию — это основная линия при построении куба. Засечками сверху и снизу слегка ограничим высоту линии. Так как линия основная, необходимо предельно точно проследить, чтобы высота этого ребра была правильной по размеру. Это очень важно.
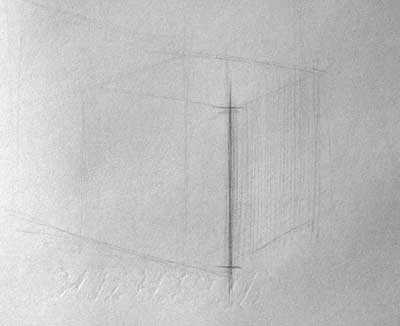
Основание куба
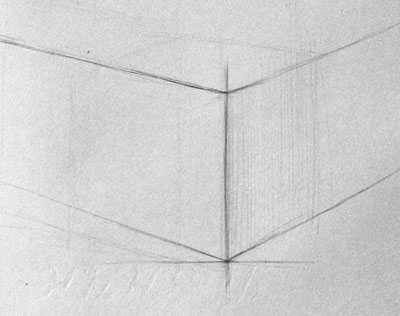
При рисовании основания куба очень важно определить углы наклона основных видимых граней, относительно основания. Это можно сделать очень простым способом: необходимо поднести карандаш на расстоянии вытянутой руки в строго горизонтальном положении к нижнему ближнему углу и запомнить углы, но не пытайтесь просто переносить углы на холст с помощью карандаша, это неправильно. Пытайтесь запомнить их и повторять. Только так будет «набиваться» рука и глазомер.
Далее необходимо учесть, что если грань куба больше развернута к вам, то угол меньше. Так можно определить какая грань меньше развернута, а какая — больше.

Можете нарисовать нижние грани, но до того, как перейти к началу рисования верхних, необходимо подумать над основным законом перспективы, который гласит, что любые параллельные линии, уходящие от зрителя, сокращаются в одну точку — точку схода.

У нашего куба имеется четыре ребра, которые смотрят направо и столько же ребер налево. Все четыре линии ребер, которые уходят влево, при их продолжении, сокращаются в одной точке схода слева, а все линии, которые уходят вправо — сходятся справа.
Но как правильно определить где все эти точки будут сходиться? Куб расположен на горизонтальной плоскости, а она параллельна поверхности земли как пол, стул и стол. И если наши линии удаляется от какого-либо предмета, то точка схода должна лежать именно на линии горизонта.
Но где же располагается линия горизонта? Всё просто: она всегда расположена на уровне глаз человека. Куда бы вы не смотрели — линия горизонта будет ровно на уровне ваших глаз. Проведите небольшое исследование: посмотрите в окно и представьте, где сходится земля с небом. Ответ будет очевиден. Даже если мы присядем, то и линия горизонта опустится.
Линию горизонта и точки схода рисуют тонкими линиями на листе до того, как нарисовать верхние грани.
Вертикальные линии и невидимые грани
Обратите внимание на снимок куба в самом начале статьи. На нем отчетливо видно, что линии, которые расположены вертикально, немного наклонены. Это, прежде всего, связано с тем, что объектив фотокамеры, с которой производился снимок, увидел перспективное сокращение линий.

И это правда, когда мы видим куб сбоку и сверху, кажется что вертикальные линии чуть-чуть сходятся в одну точку которая располагается снизу. Академический рисунок игнорирует передачу сокращения вертикальных линий, за исключением случаев сильного ракурса, а при начальном уровне обучения, куб рисуется с параллельными вертикальными линиями, строго перпендикулярными линии горизонта.
Как только нарисованы верхние линии, проверяем, насколько сократились боковые грани с обеих сторон. Ширину данных граней меряем только по горизонтали, ни в коем случае не под наклоном, и переходим к сравниванию, какая из них меньше высоты самого ближнего бедра куба, и обязательно без между собой. Как только закончите с проверкой ближних линий и вертикальных ребер можете приступать к зарисовке дальних уходящих линий.
Невидимые линии также обязательно следует рисовать. Перед тем, как будете рисовать самое дальнее вертикальное бедро, убедитесь, что их точки схода расположены правильно. Если они расходятся и это заметно, то необходимо еще раз все тщательно проверить и исправить рисунок, самое главное не испортить его. Если расхождение линий не такое большое, необходимо просто немного подкорректировать линии и нарисовать дальше бедро, которое будет располагаться вертикально.
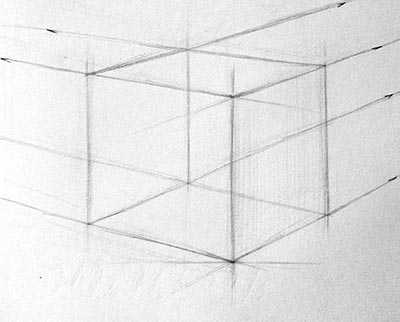
Как только, вы закончили с построением, выделите ближние к себе линии. Если линия темная — будет казаться, что она ближе. Зная это, можно передать пространство и объем.
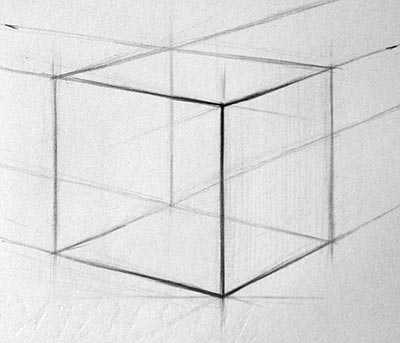
Выделение ближних линий и штриховка
Главная задача штриховки — передать объем предметов. К штриховке нельзя приступать, если рисунок выполнен неправильно. Лучше начать заново или попытаться исправить текущий.
На кубе мы можем увидеть всего три плоскости — это верхняя и две боковые грани. Визуально каждая из граней уходит от смотрящего в пространство. Для того, чтобы показать форму, необходимо штриховать грани куба так, чтобы смотрящему было очевидно, что они действительно отдаляются.
Для того чтобы передать пространство применяются законы воздушной перспективы. Темные цвета светлеют в дали, а светлые — наоборот темнеют.

Может показаться, что куб настолько мал, что влияние воздушной перспективы незаметно, но мы должны рисовать руководствуясь законами, только соблюдая их куб станет объемным.
Сама штриховка начинаем строго с теневой части. У нашего куба грань справа в тени, поэтому начнем именно с нее. Штрихуем от себя. По мере удаления плоскости в пространстве нажим на карандаш слабее, это делает штрих светлее. Штриховка может быть как вертикальной, так и горизонтальной.
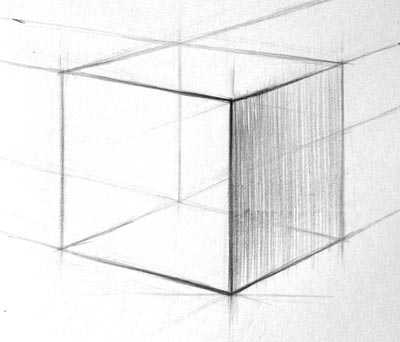
Осветленную левую часть штрихуем от себя, при этом левый угол оставляем белым, но слегка штрихуем дальнюю часть.
Верхнюю поверхность делаем как полутон (промежуточное состояние между тенью и светом). Теперь оценим ее, задаваясь вопросом: «Она скорее светлая или темная?»
Всегда можно усилить тень, введя еще штрих, направленный строго по диагонали, также необходимо его растягивать — от темного к светлому. Подчеркиваем форму, делая тональные акценты, для этого можно использовать штриховку в разные стороны.

Не стоит забывать про тень от куба, которая расположена на плоскости, на которой он находится. Падающая тень на порядок темнее тени собственной. Плюс она граничит с рефлексом от освещенной плоскости (рефлекс — свет или цвет, отраженный от соседних поверхностей. Рефлекс тем светлее, чем источник отражающего света ярче и гораздо ближе).
Зеленый, красный и серый рефлексы на белом шаре.
Рисование других геометрических тел
Как только, вы почувствуете, что овладели навыками рисования куба — можно переходить на следующий уровень и рисовать другие геометрические фигуры. Полезнее всего рисовать их не в «одиночку» а группой. Для начала число геометрических фигур берите небольшое, примерно 2−3 фигуры.

При всем этом не забывайте, что фигуры нужно не просто копировать, а рисовать с учетом всех правил построения.
Я искренне надеюсь, что вам понравился урок о том, как нарисовать куб, надеюсь было интересно и познавательно. Теперь можете обратить внимание на урок «Как нарисовать льва» — он такой же интересный и увлекательный. Ну и кнопки социальных сетей тут не просто так =)
www.plusphotoshop.ru

 Рисование куба — следующий этап в освоении техники академического рисунка. Из геометрических фигур куб является самой простой для начинающих. На примере изображения формы куба на занятиях по рисунку я объясняю правила линейной и воздушной перспективы, правильные приёмы штриховки, передачу объёмной формы предметов.
Рисование куба — следующий этап в освоении техники академического рисунка. Из геометрических фигур куб является самой простой для начинающих. На примере изображения формы куба на занятиях по рисунку я объясняю правила линейной и воздушной перспективы, правильные приёмы штриховки, передачу объёмной формы предметов.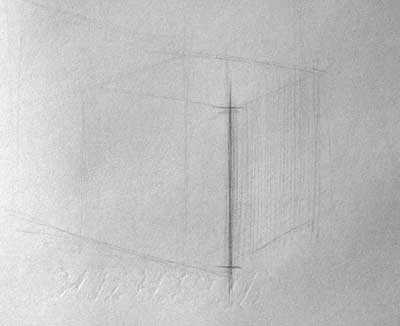


Leave a Comment