Симметричные рисунки по геометрии: Презентация по геометрии по теме «Предметы, фигуры симметричные относительно оси».

18.06.2021 Facebook Twitter LinkedIn Google+ Разное

Содержание

Презентация по геометрии по теме «Предметы, фигуры симметричные относительно оси».

Инфоурок › Геометрия ›Презентации›Презентация по геометрии по теме «Предметы, фигуры симметричные относительно оси».

Скрыть

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Двусторонняя симметрия — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны.

2 слайд Описание слайда:

Посмотрите на снежинку, бабочку, листок. Что объединяет эти рисунки?

3 слайд Описание слайда:

Если сложить пополам снежинку, бабочку, листок вдоль прямой, то её части совпадают.

4 слайд Описание слайда:

Вокруг нас встречаются симметричные предметы. Если у предмета совпадают правая и левая сторона при сгибании, то такие предметы называются симметричными. Прямая, вдоль которой согнут предмет, называется осью симметрии

5 слайд Описание слайда:

Если у предмета совпадают правая и левая сторона при сгибании,то такие предметы называются симметричными. Прямая, вдоль которой согнут предмет, называется осью симметрии

6 слайд Описание слайда:

Если предметы симметричны относительно прямой (оси симметрии), то такая симметрия называется осевая симметрия

7 слайд Описание слайда:

Все ли предметы являются симметричными , относительно прямых? Если у предмета совпадают правая и левая сторона при сгибании, то такие предметы называются симметричными. Прямая, вдоль которой согнут предмет, называется осью симметрии

8 слайд Описание слайда: 9 слайд Описание слайда:

А Y В Х Задание: № 355

10 слайд Описание слайда:

Prezentacii.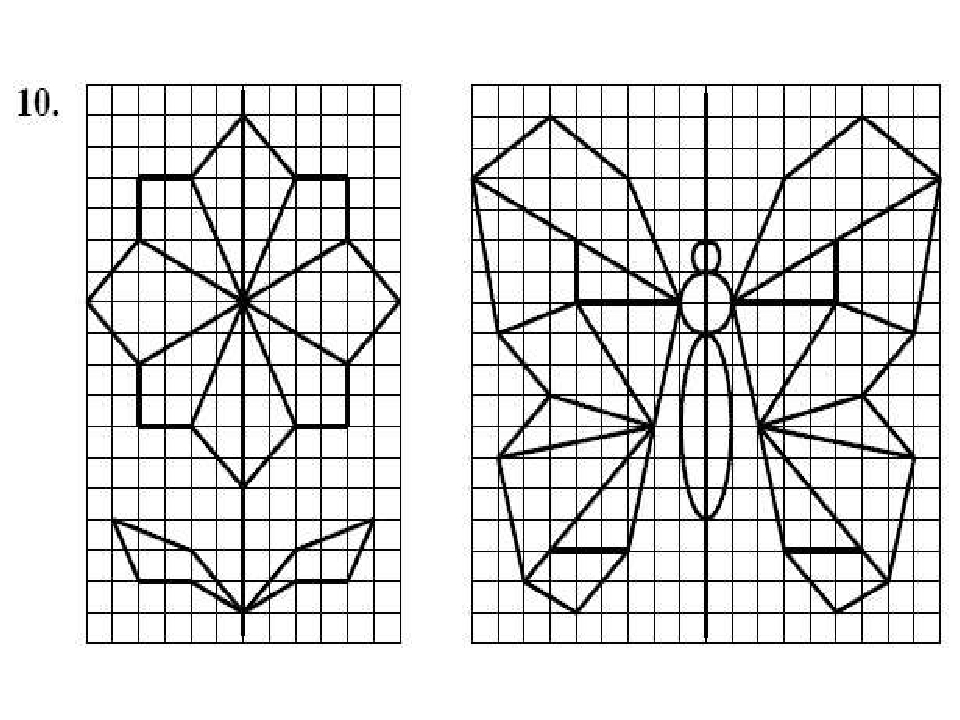 com

11 слайд
Описание слайда:

Симметрия в природе Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.

12 слайд Описание слайда:

Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.

13 слайд Описание слайда:

Симметрия у животных

14 слайд Описание слайда: 15 слайд Описание слайда:

Симметрия в животном мире.

16 слайд Описание слайда: 17 слайд Описание слайда: 18 слайд Описание слайда: 19 слайд Описание слайда: 20 слайд
Описание слайда:

Симметрия у растений

21 слайд Описание слайда: 22 слайд Описание слайда: 23 слайд Описание слайда: 24 слайд Описание слайда: 25 слайд Описание слайда:
26 слайд Описание слайда: 27 слайд Описание слайда: 28 слайд Описание слайда: 29 слайд Описание слайда: 30 слайд Описание слайда: 31 слайд
Описание слайда:

Пирамида Хеопса Египет Собор Парижской Богоматери Франция Тадж Махал Турция Биг Бэн Великобритания Эйфелева Башня

32 слайд Описание слайда: 33 слайд Описание слайда:

Симметрия в архитектуре России Казанский собор Зимний Дворец Останкинская башня Кремль Разводной мост Исаакиевский Собор

34 слайд Описание слайда: 35 слайд Описание слайда:

Снежинка – это группа кристалликов, образованная более чем из двухсот ледяных частичек.

Симметрия – это свойство кристаллов совмещаться друг с другом в различных положениях путём поворотов, параллельных переносов, отражений.

36 слайд Описание слайда: 37 слайд Описание слайда:

Многим творениям человеческих рук умышленно придается симметричная форма как из эстетических, так и практических соображений.

38 слайд Описание слайда:

В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, одинаковость в расположении частей».

39 слайд Описание слайда: 40 слайд Описание слайда: 41 слайд Описание слайда: 42 слайд Описание слайда:

Два кольца, два конца, А посередине – гвоздик. Можно ли назвать ножницы симметричной фигурой? Почему?

43 слайд Описание слайда:

Хвост на дворе, Нос в конуре. Кто хвост повернёт, Тот и в дом войдёт Можно ли назвать ключ симметричной фигурой? Почему?

44 слайд Описание слайда:

Можно ли назвать стрекозу насекомым, у которого имеется ось симметрии? На ромашку у ворот Опустился вертолёт – Золотистые глаза. Кто же это?…

45 слайд Описание слайда: 46 слайд Описание слайда:

Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция

47 слайд Описание слайда:

Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб

48 слайд Описание слайда:

Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг

49 слайд Описание слайда: 50 слайд Описание слайда: 51 слайд Описание слайда:

Квадрат, круг, равнобедренный треугольник – симметричные геометрические фигуры. Прямая, которая делит их на равные половины называется осью симметрии.

52 слайд Описание слайда:

«5» «4»

53 слайд Описание слайда:

Симметричные фигуры Несимметричные фигуры

54 слайд Описание слайда:

Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии

55 слайд Описание слайда:

Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии Квадрат – 4 оси симметрии

56 слайд Описание слайда:

Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии Квадрат – 4 оси симметрии Параллелограмм Круг – бесконечное количество осей симметрии

57 слайд Описание слайда:

Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии Квадрат – 4 оси симметрии Параллелограмм

58 слайд Описание слайда:

Найдите признак, по которому данные фигуры можно разбить на две группы. I группа (1, 4, 6) – фигуры, которые имеют две оси симметрии; II группа (2, 3, 5) – фигуры, которые имеют более двух осей симметрии. Что такое ось симметрии?

59 слайд Описание слайда:

Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник

60 слайд Описание слайда:

Буквы русского алфавита имеют оси симметрии

61 слайд Описание слайда: 62 слайд Описание слайда:

Существуют даже слова, имеющие ось симметрии МАДАМ КОК ФОКС НОС

63 слайд Описание слайда:

В Е Ж З К Н О С Ф Х Э Ю

64 слайд Описание слайда:

А Д Ж Л М Н О П Т Ф Х Ш

65 слайд Описание слайда:

Б Г И Р У Ц Ч Я Щ

66 слайд Описание слайда:

Я в листочке, я в кристалле, Я в живописи, архитектуре, Я в геометрии, я в человеке. Одним я нравлюсь, другие Находят меня скучной. Но все признают, что Я — элемент красоты.

67 слайд Описание слайда: 68 слайд Описание слайда: 69 слайд Описание слайда:

1) Рассмотри рисунки. Есть ли такие предметы, у которых может быть несколько осей симметрии. 2) Догадайся! На каком рисунке точки симметричны относительно данной прямой. Как это проверить?

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-273068

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

определение, свойства, обозначение, фигуры обладающие симметрией

Что такое осевая симметрия в геометрии 

Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.

Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:

Sn (А) = В.

Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.

Свойства осевой симметрии

  1. Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
  2. Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
  3. Обратное преобразование осевой симметрии есть та же осевая симметрия.
  4. Осевая симметрия – это поворот относительно оси симметрии на 180°.

Теорема и доказательство

Теорема

Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется. 

Если отрезок MN симметричен отрезку M1N1  относительно прямой a, то MN = M1N1. 

Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:

  • P – это точка пересечения MM1 и прямой a;
  • Q – это точка пересечения NN1 и прямой a; 
  • построим отрезок MK, перпендикулярный NN1;
  • тогда точка K отразится в точку K1.

Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

МК = М1К1 , так как перпендикулярны к параллельным прямым.

По построению:

NK = NQ – KQ,

N1K1 = N1Q – K1Q. 

Точка N отобразилась в точку N1,  значит:

NK = N1K1.

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть  MN = M1N1, что и требовалось доказать.

Фигуры, обладающие симметрией

Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Пример №1

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:

  • AO – общая сторона
  • Из свойства биссектрисы: ∠ MAO = ∠KAO
  • Треугольники KAO и MAO прямоугольные,

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

Пример №2

Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

Пример №3

У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Пример №4

Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Пример №5

Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

Пример №6

У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы. 

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

что называется, какие фигуры обладают, свойства

Понятие

Определение

Центральная симметрия — это свойство фигуры, у которой есть некоторые точки В и В1, соединяющие отрезок и совпадающие в пространстве относительно фиксированного элемента — центральной точки С.

Симметричными могут быть и части фигуры. Для этого они должны быть соразмерными относительно центра. То есть при предполагаемом сгибе фигуры по центру все точки двух половин должны совпасть в пространстве.

Свойства

Одно из свойств симметрии — движение. Это значит, что при изменении положения все точки окажутся на том же расстоянии друг от друга, что и были, то есть симметрия сохранится.

Примечание

Изменение в пространстве предполагает поворот фигуры на 180°.

Центральная точка симметрии всегда неподвижна.

Прямая, проходящая через центр, симметрична сама себе.

Если прямая не проходит через центр, то она является параллельной. Это можно доказать путем построения двух прямых параллельных друг другу с центральной точкой, не лежащей ни на одной из линий. Соединяя симметричные точки, получим два равнобедренных треугольника, которые лежат накрест, а основания их останутся параллельными.

 

Формула

Так как точка симметрии является центральной, то отрезки прямой, симметричные относительно этой точки, должны быть равны. Представим линию, соединенную точками А и В. Центром пусть будет Х. Верным можно считать равенство АХ=АВ. Если происходит движение, то А переходит в точку А1, а В в В1. Центральная точка Х остается неподвижной. В этом случае АВ = А1В1.

Фигуры с центральной симметрией

К таким фигурам относится параллелограм, так как в центральной точке пересекаются его диагонали. Каждая из фигур, получившаяся в результате пересечения, является симметричной.

У окружности центр находится посередине, а точки, лежащие на ней, являются симметричными.

Аналогичными свойствами обладают ромб и квадрат.

Как построить

Для построения симметрии относительно центральной точки, нужно начертить линию. Затем от одной из точек отложить отрезок, равный расстоянию между двумя первыми точками, и отметить третью. В результате вторая точка станет центром симметрии.

Примеры

Центральная симметрия часто встречается в окружающих нас предметах. В природе это любые круглые предметы: плоды кокоса, арбуза, томата, шапка одуванчика. Цветы симметричны относительно своей центральной части. Пчелиные соты представляют собой идеальные ромбы. Микроскопические капли воды, замерзая, образуют симметричные снежинки.

Симметрия свойственна многим предметам, созданным человеком: колесо, дорожные знаки, начертание букв.

Все виды симметрии, и центральная в частности, находят применение в строительстве и архитектуре. Принципа соразмерности придерживались все сторонники классицизма в искусстве.

Математика (3-й класс). Симметрия. Как нарисовать симметричный предмет

Рисуем симметричный предмет

Следим, чтобы получилось как можно более похоже. Для этого будем буквально строить нашу половинку. Не подумайте, что так легко, тем более с первого раза, одним росчерком провести зеркально-соответствующую линию!

Разметим несколько опорных точек для будущей симметричной линии. Действуем так: проводим карандашом без нажима несколько перпендикуляров к оси симметрии – средней жилке листа. Четыре-пять пока хватит. И на этих перпендикулярах отмеряем вправо такое же расстояние, какое на левой половине до линии края  листика. Советую пользоваться линейкой, не очень-то надейтесь на глазок. Нам, как правило, свойственно уменьшать рисунок – на опыте замечено. Отмерять расстояния пальцами не порекомендуем: слишком большая погрешность.

Полученные точки соединим карандашной линией:

Теперь придирчиво смотрим – действительно ли половины одинаковы. Если всё правильно – обведём фломастером, уточним нашу линию:

 Лист тополя дорисовали, теперь можно  замахнуться и на дубовый.

Нарисуем симметричную фигуру

В этом случае сложность заключается  в том,что обозначены жилки  и они не перпендикулярны оси симметрии и придётся не только размеры но ещё и угол наклона точно соблюдать. Ну что ж – тренируем глазомер:

Вот и  симметричный лист дуба нарисовался, вернее, мы его построили по всем правилам:

Изучаем зеркальную симметрию 

По своей природе, ребенок не может сразу изобразить две половинки одного целого одинаково. Рисунки маленьких детей почти всегда корявые и ассиметричные. Поэтому, когда мы изучаем зеркальную симметрию нужно объяснить ребенку, что половинки каждого из окружающих его предметов, как и собственное тело малыша, симметричны. Для подобного стартового этапа изучения симметрии подойдет упражнение с рисунком половины знакомого ребенку предмета красками впритык к сгибу альбомного листа и его перебивание на другую половину таким образом, чтоб получился целый предмет. Увидев результат полученной работы, объясните ребенку, что целый мячик, яблочко или что-либо изображенное, получилось из нарисованной половинки и есть отображение симметрии в предмете. Такие рисунки будут научным пособием для юного ученика о важности симметрии в окружающей его реальности.

Симметрия для детей

Другой разновидностью упражнений, которые входят в практические задания учимся рисовать симметрично являются упражнения, в которых мы с ребенком изучаем симметрию по точкам. Для формирования твердости руки и четкости движений ребенка, которые важны для четкого формирования рисунка попросите дошкольника соединить поставленные Вами точки в силуэт знакомого малышу предмета. Таким образом симметрия для детей станет более понятной и внедриться в реальный мир с помощью знакомых и интересных ребенку карандашей и красок.

Практические задания по симметрии 

Для облегчения обучения принципам одинаковости половинок рисунка можно распечатать симметрические рисунки для ребенка и проводить занятия по этим шаблонам. На нашем сайте подобраны одобренные педагогами детских центров раннего развития рисунки симметрии распечатать которые можно дома и дальше проводить занятия с включением этих дополнительных материалов. Материалы сайта Childdevelop характеризуются понятностью и доступностью для маленьких детей, учитывают особенности восприятия процесса обучения в детском возрасте и мелкой моторики. Практические задания по симметрии скачать бесплатно можно у нас и быстро получить от обучения результат, который порадует как школьными успехами, так и множеством красивых рисунков.

центральная симметрия

    Две точки называются симметричными относительно центра симметрии О, если О – середина отрезка, соединяющего эти точки. Точка О считается симметричной самой
себе.

Геометрическая фигура (или тело) называется симметричной относительно центра О, если для каждой точки этой фигуры может быть найдена другая точка  этой же фигуры, так что отрезок,
соединяющий эти точки, проходит через центр О и делится в этой точке пополам. Точка О называется центром симметрии.

поворотная симметрия (симметрия вращения)

   При поворотной симметрии переход частей фигуры в новое положение или преобразование исходной фигуры происходит при повороте  фигуры на определенный угол вокруг точки,
которая называется центром поворота. Поворотная симметрия может рассматриваться на плоскости и в пространстве.

Тело (фигура) обладает симметрией вращения, если при повороте на угол 360°/n  (n – целое число, например, 2, 3, 4 и т.д. до бесконечности) вокруг некоторой прямой (оси симметрии) оно
полностью совпадает со своим начальным положением. При n = 2 мы имеем  осевую симметрию.

симметрия подобия

Представляет собой своеобразный аналог предыдущих симметрий с той лишь разницей, что она связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между
ними. Простейшим примером такой симметрии являются матрешки.  

переносная (трансляционная симметрия)

О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние, либо расстояние, кратное этой величине, она совмещается сама с собой. Прямая, вдоль которой
производится перенос, называется осью переноса. 

примеры симметрии геометрических фигур

   Разными видами симметрии могут обладать и плоские и объемные фигуры. Например, квадрат, прямоугольник, ромб имеют и центр симметрии и оси симметрии.

Окружность и круг имеют центр симметрии и бесконечно много осей симметрии. Объемные фигуры могут иметь центр симметрии, оси симметрии и обладать зеркальной симметрией.

Правильные многогранники своей симметрией с древних времён привлекали к себе внимание учёных, архитекторов, художников. Их по праву называют самыми симметричными из всех
многогранников.

Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона. Правильным многогранникам посвящена 13 книга “Начал”
Евклида.

   Очень симметричной фигурой является, например, куб. Центром симметрии куба является точка пересечения его диагоналей.  Через центр симметрии проходят  9 осей
симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).

 Через центр симметрии проходят  9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных
ребер (3).



Как включить симметричные фигуры в Photoshop

Инструмент Paint Symmetry помогает рисовать зеркальные изображения в любой плоскости. Как следует из названия, эта функция работает с инструментами Paintbrush, Pencil и Eraser. Значок бабочки на панели инструментов говорит о том, что функция симметрии краски активна. Но как вы активируете эту скрытую функцию в Photoshop?

  1. Откройте Фотошоп. Идти к Настройки> Технологические обзоры и проверить Включить симметрию краски. Закройте диалоговое окно.
  2. Выберите инструмент «Кисть», «Карандаш» или «Ластик».
  3. Нажмите на бабочка значок в Панель настроек и выберите один из типов симметрии из меню.
  4. Нажмите Enter или установите флажок, чтобы установить оси симметрии на холсте.
  5. Рисуйте с помощью инструментов Paintbrush или Pencil. Тип симметрии, который вы выберете, будет определять вид зеркальных штрихов на холсте.

Что такое графический диктант

Необычные дидактические занятия нравятся дошкольникам. Они не требуют от ребенка глубоких знаний, сильного напряжения ума. К таким методам работы относятся и графические диктанты по клеточкам.

Это игра, в процессе которой ребенок рисует линии, диагонали на листе бумаги и в результате получает картинку.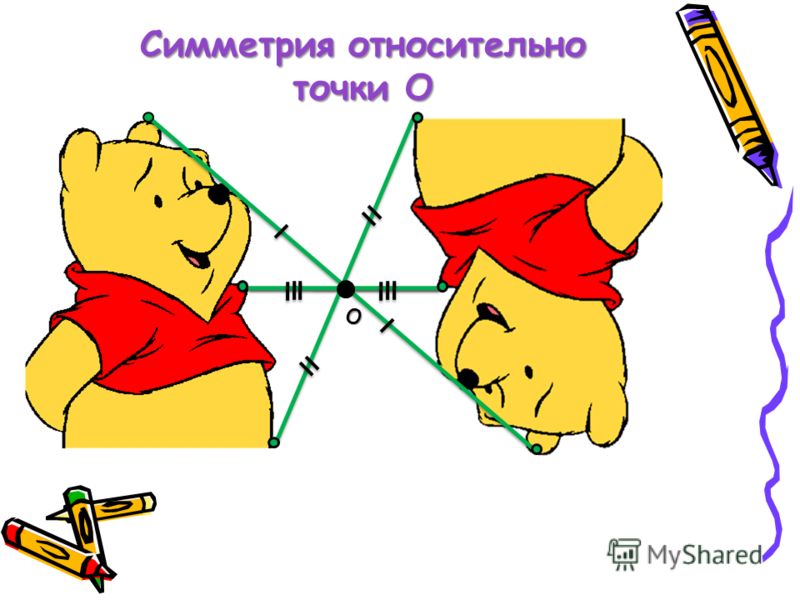 Делать это несложно. Нужно только внимательно слушать педагога, проводить карандашом черточки влево, вправо, вверх или вниз. Развивая моторику, малыш учится считать, ориентироваться в пространстве, оценивать себя и радоваться успехам однокашников.

Если дошкольник зазевается, отвлечется, то картинка не сложится. Ребенок осознает важность настроенности на урок, бдительности и серьезности в процессе будущего обучения в школе.

Для графических диктантов используют простые картинки. Например, домик, собака, машина. Изображения должны быть знакомы малышам, не требовать длительного времени исполнения.

Польза математических диктантов

Графический диктант для дошкольников — полезная методика для диагностики уровня развития и занятий по подготовке к школе в детском саду, дома.

В ДОУ воспитатели чаще используют пособия авторов: Д.Б. Эльконина, О.А. Холодовой. К.В. Шевелев разработал целый курс поэтапных занятий с детьми 4–5 лет, 5–6 лет, а также первоклассниками. Специальные тетради развивают следующие навыки и умения у дошколят из подготовительной группы:

  • координация движений;
  • внимание;
  • память;
  • усидчивость;
  • воображение;
  • словарный запас;
  • мелкая моторика;
  • орфографическая зоркость.

Одновременно с физическими навыками ребенок повышает самооценку. Он осознает необходимость восприятия инструкции на слух. Делает работу четко и быстро, не отвлекаясь на птичку в окошке или смех соседа по парте.

Еще одной задачей графической математики является расширение кругозора. Подбирать картинки нужно по возрасту и уровню развития малышей, но это только на первых порах. Позже рисуйте изображения, которые незнакомы дошкольникам. После начертания такой арифметической задачи на листе бумаги расскажите историю о необычном животном, познакомьте с местом обитания, покажите фотографию.

Числовые задания под диктовку хорошо адаптируют детсадовцев к школе. Учат шестилеток самостоятельности, ориентированию в новом пространстве. Это поможет в освоении программы начальной школы, при знакомстве с новым коллективом, педагогом.

Умение держать карандаш, выполнять устные инструкции, расшифровывать текст, писать – отличная база для подготовки к первому классу. Можно попросить ребенка распечатывать листы, шаблоны, помочь в интерпретации инструкции. Это помогает познакомить будущего дошкольника с офисной техникой, воспитать уважение к старшим.

Правила выполнения

Графические диктанты лучше использовать на математических уроках, например в 1 классе. Выполнение связано с системой координат, счетом, геометрическими фигурами. Методика проведения состоит из нескольких этапов:

  1. Подготовьте для ученика лист бумаги в клеточку. У себя держите готовый вариант диктанта.
  2. Поставьте точку на ученическом листке. Это будет начало отсчета. Или попросите дошкольника сделать это самостоятельно, объяснив, сколько места нужно отступить.
  3. Нарисуйте на бумаге для ребенка, только начинающего обучение, стрелочки, которые указывают направления сторон. Так легче получить правильный результат. На последующих занятиях подсказки уже не понадобятся.
  4. Объясните, что 1 шаг – это клетка. Если делаем 2 шага, линия проходит 2 клетки.
  5. Учитель диктует условия работы поэтапно.

На готовом листе для педагога есть рисунок, координатная плоскость, состоящая из стрелок, цифр. Например, чтобы нарисовать елочку, проложите линию по горизонтали в 1 клеточку, по вертикали – 3 клеточки, наискосок – 3 клеточки и так далее. Чаще это просто стрелочки и цифры без слов.

Педагог проговаривает, какие линии, куда, на какое расстояние чертят дошкольники. Инструкции даются друг за другом, не торопясь.

  1. После выполнения письменных заданий, получения результата сделайте выводы об уроке, стараниях дошкольников. Пожурите за невнимательность, если ребенок отвлекался по пустякам, или похвалите за достижения.

Важно! Нельзя торопиться. Если дошколенок не успевает, чаще на первых занятиях, подождите его.

Пропуск даже одного шага или неверное начертание испортят готовый результат. Временные рамки устанавливайте постепенно, ускоряя процесс на пару секунд от урока к уроку.

Источники

  • http://handykids.ru/kak-narisovat-simmetrichnyj-predmet/
  • https://childdevelop.ru/worksheets/tag-math-symmetry1/
  • https://kozelrozel.jimdofree.com/%D1%8D%D1%82%D0%BE%D1%82-%D1%83%D0%B4%D0%B8%D0%B2%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE-%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D1%8B%D0%B9-%D0%BC%D0%B8%D1%80/%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F-%D0%B2-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5/%D0%B2%D0%B8%D0%B4%D1%8B-%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8/
  • http://helpexe.ru/tvorcheskij/kak-risovat-idealno-simmetrichnye-figury-v
  • https://razvitie-vospitanie.ru/intellect/graficheskij_diktant.html

Презентация к уроку геометрии по теме «Осевая и центральная симметрия» | Презентация к уроку по геометрии (7, 8, 9 класс) на тему:

Слайд 1

СИММЕТРИЯ

Слайд 2

Слово «симметрия» (symmetria) происходит от греческого «сим» — с, вместе и «метрон» — мера, буквально означает соразмерность, одинаковость в расположении частей чего-либо относительно точки, прямой, плоскости.

Слайд 3

Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г. Вейль

Слайд 4

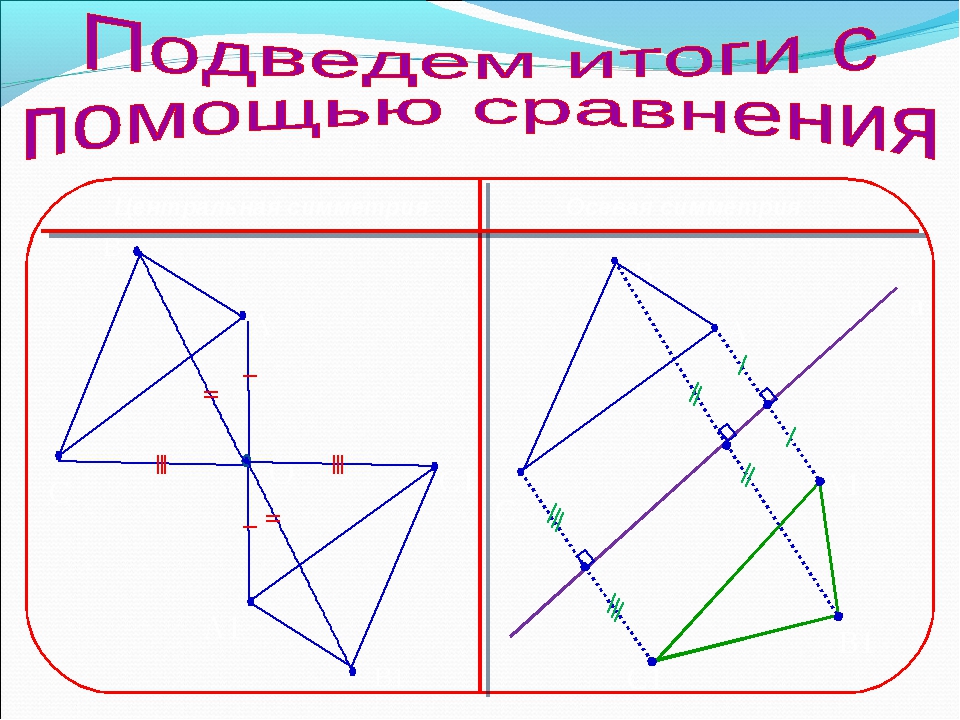
СИММЕТРИЯ Две точки А и А1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе. Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.

Слайд 5

1.Опустить перпендикуляр из точки А на прямую l. А В l 2.Продолжить перпендикуляр на такое же расстояние, поставить точку В 3. Полученная точка В будет симметрична данной точке А. ОСЕВАЯ СИММЕТРИЯ

Слайд 6

В отличии от слова «ЧАЙ» слово «КОФЕ» обладает горизонтальной осью симметрии, поэтому оно не искажается при отражении в зеркале ОСЕВАЯ СИММЕТРИЯ

Слайд 7

А М Т Ш П В З К С Э Е Ж Н О Ф Х ОСЕВАЯ СИММЕТРИЯ

Слайд 8

У неразвернутого угла одна ось симметрии – прямая, на которой расположена биссектриса угла ОСЕВАЯ СИММЕТРИЯ

Слайд 9

Равнобедренный треугольник имеет одну ось симметрии. Равносторонний треугольник – три оси симметрии ОСЕВАЯ СИММЕТРИЯ

Слайд 10

Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат – четыре оси симметрии ОСЕВАЯ СИММЕТРИЯ

Слайд 11

У окружности осей симметрии бесконечно много – любая прямая, проходящая через ее центр, является осью симметрии У параллелограмма, отличного от прямоугольника, и разностороннего треугольника нет ни одной оси симметрии ОСЕВАЯ СИММЕТРИЯ

Слайд 12

Точки А и А1 называются симметричными относительно точки О, если О середина отрезка АА1 . . . А О А1 . . М М1 . . N N1 N симметрична N1 , т.к. N О = О N1 М не симметрична М1, т.к. МО ≠ ОМ1 О симметрична сама себе ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Слайд 13

… . Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре . . А А1 О О – центр симметрии ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Слайд 14

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ О О Центром симметрии окружности является центр окружности. Центр симметрии параллелограмма – точка пересечения его диагоналей

Слайд 15

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Ответьте на вопрос: обладает ли центральной симметрией прямая? У прямой бесконечное множество центров симметрии (любая точка прямой является ее центром симметрии)

Слайд 16

СИММЕТРИЯ В ПРИРОДЕ Симметрия присуща различным видам растений и грибам, и их частям, а также большому количеству видов животных и насекомых.

Слайд 17

Центральная симметрия характерна для цветов плодов растений. Рассмотрим разрез любой ягоды. В разрезе она представляет собой окружность, а окружность имеет центр симметрии. СИММЕТРИЯ В ПРИРОДЕ

Слайд 18

СИММЕТРИЯ В ПРИРОДЕ Самым ярким примером красоты форм симметрии являются кристаллы и снежинки. Мало кто знает, что природные снежинки бывают только шестиугольными или любыми другими образованиями с количеством лучей, кратным трем.

Слайд 19

СИММЕТРИЯ В АРХИТЕКТУРЕ Примером современных зданий, построенных в середине ХХ века, является гостиница “Прибалтийская”. Симметричность, как видно из рисунка присутствует как в общей композиции, так и в каждой из трех его составляющих В начале XIX века по проекту А.Н. Воронихина было сооружено выдающееся произведение искусства – Казанский собор, имеющий четкие симметричные композиции

Слайд 20

СИММЕТРИЯ В БЫТУ Издревле люди стремились украсить все, что окружало их в быту. Они придумывали удивительные замысловатые орнаменты, в построении которых часто используются принципы симметрии, приёмы ритмичных повторов.

Слайд 21

СИММЕТРИЯ В ИССКУСТВЕ Симметричная композиция легко воспринимается зрителем, сразу привлекая внимание к центру картины, в котором и находится то главное, относительно которого разворачивается действие.

Слайд 22

Природа говорит языком математики : буквы этого языка — круги, треугольники и иные математические фигуры. Галилей.

Слайд 23

http://thebestartt.com/snejinka-klipart http://www.dizayne.ru http://photoclub.by/work.php?id_photo=255181&id_auth_photo=2645 http://vpiter.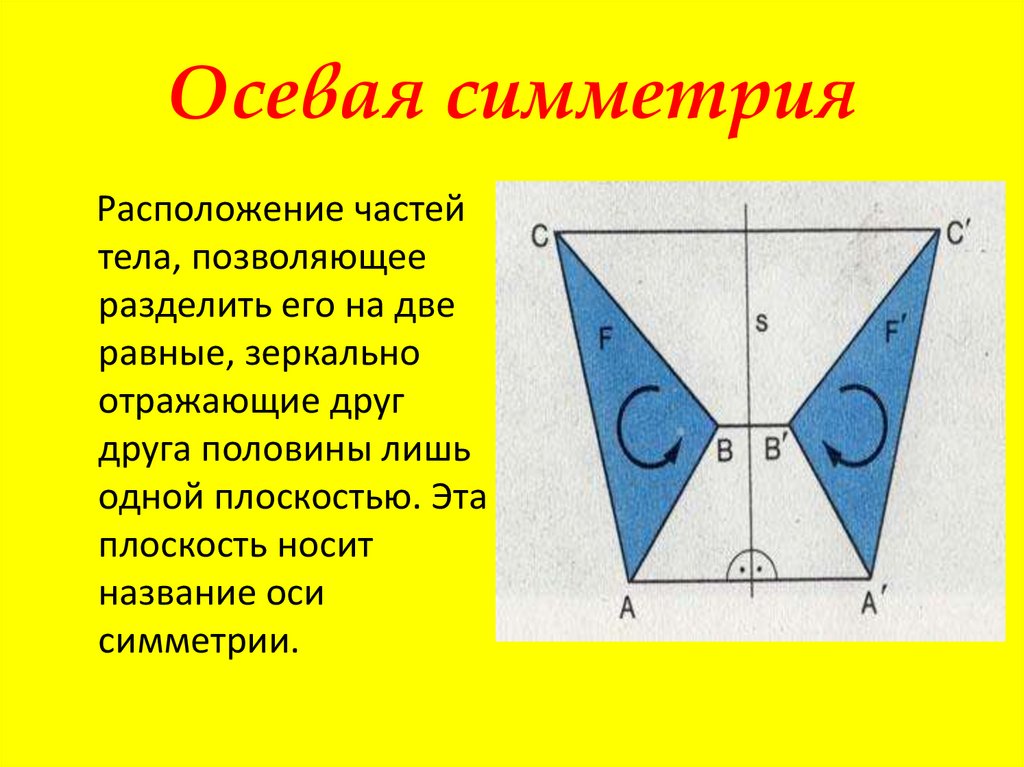 com/pribaltiiskaya_com/ http://greensector.ru/stroitelstvo-i-remont/nalichniki-na-okna-v-chastnom-dome-varianty-izgotovlenie-svoimi-rukami.html http://www.bugaga.ru/pictures/1146725751-zhivopisnye-otrazheniya-v-vode.html http://mimege.ru/search/apelsin-razrez

Осевая симметрия | Треугольники

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

1) Провести из точки A к прямой g перпендикуляр AO.

 

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.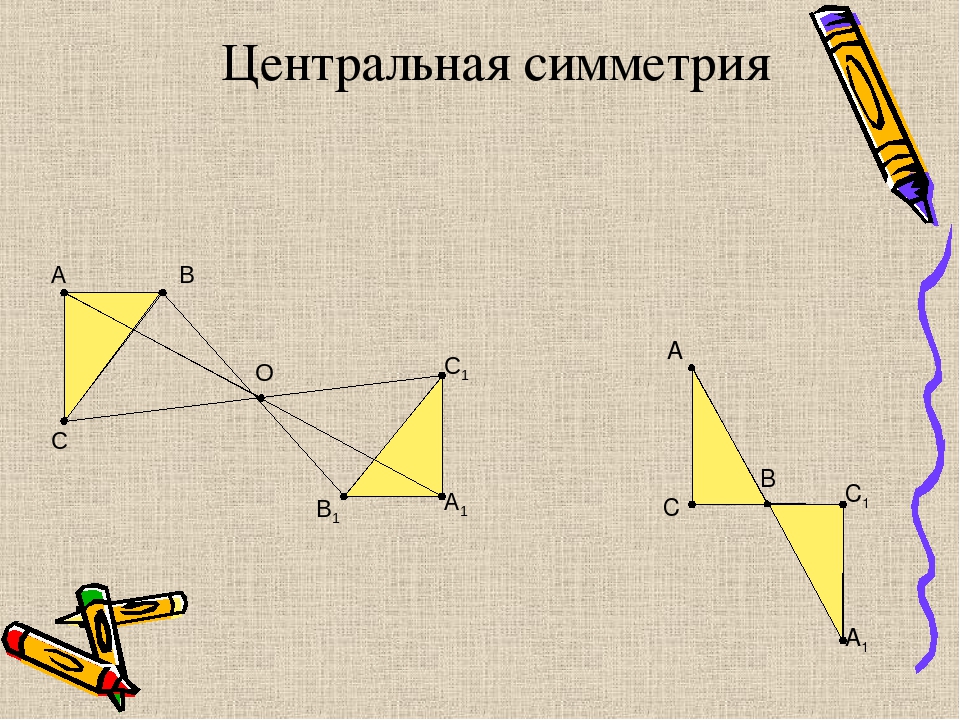

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F  в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.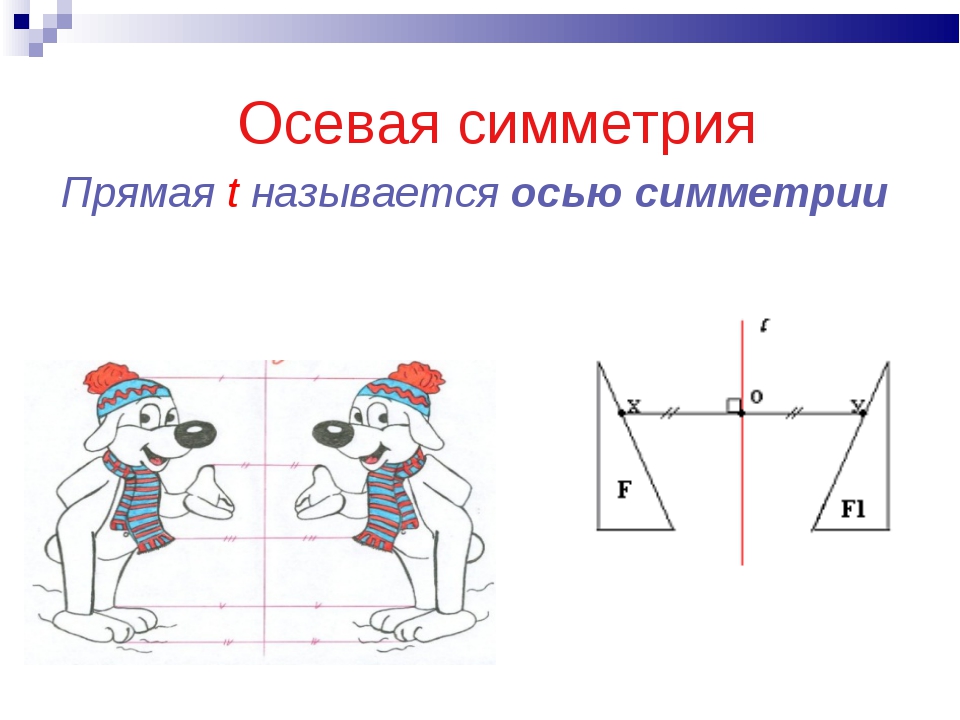

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

2) Ромб.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

4) Окружность.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

5) Прямая.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

6) Равнобедренная трапеция.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

7) Равнобедренный треугольник.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

 

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

 

9) Угол.

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

 

Теорема.

Осевая симметрия является движением.

Геометрия

Геометрия — это всего около фигур и их свойства.

Если вам нравится играть с объектами или рисовать, то геометрия для вас!

Геометрию можно разделить на:


Плоская геометрия — это плоские формы, такие как линии, круги и треугольники … формы, которые можно нарисовать на листе бумаги


Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.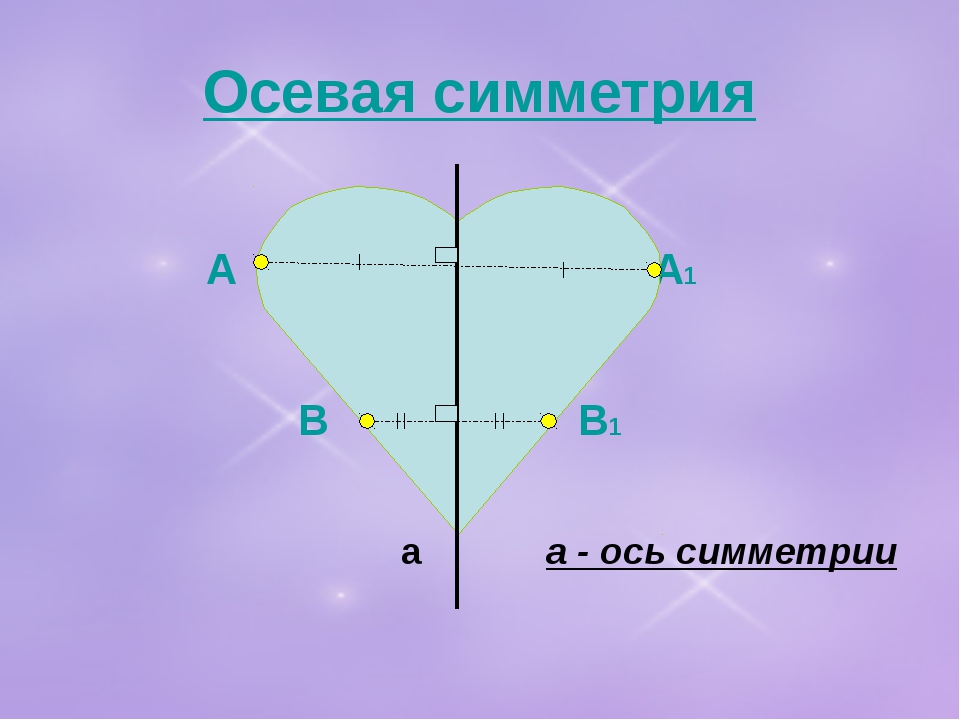

Подсказка: попробуйте нарисовать некоторые формы и углы по мере изучения … это помогает.

Точка, линия, плоскость и твердое тело

Точка не имеет размеров, только позиция
Линия одномерная
Самолет двумерный (2D)
Твердое тело трехмерное (3D)

Почему?

Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать мир вокруг нас.

Плоская геометрия

Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).




Полигоны

Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.

Вот еще несколько:

Круг

Теоремы о круге (расширенная тема)

Символы

В геометрии используется много специальных символов.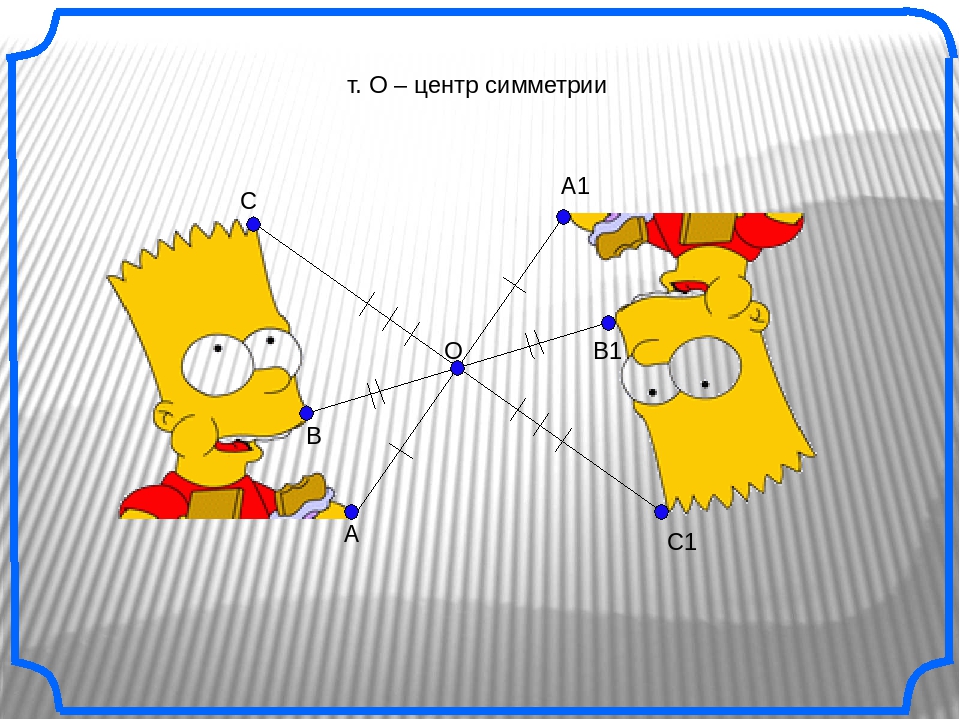 Вот вам краткая справка:

Геометрические символы

Конгруэнтные и похожие

Уголки

Типы углов

Преобразования и симметрия

Преобразований:

Симметрия:


Координаты

Дополнительные разделы по геометрии плоскости

Пифагор

Конические секции

Теоремы о круге

Центры треугольника

Тригонометрия

Тригонометрия — отдельная тема, поэтому вы можете посетить:

Твердая геометрия

Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…

… начнем с самых простых форм:


Общие 3D-формы

Многогранники и неполигранники

Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:

Многогранники (должны иметь плоские грани) :

Мы не можем найти эту страницу

(* {{l10n_strings. REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings. LANGUAGE}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Лучший набор геометрии для рисования — отличные предложения по набору геометрии для рисования от глобальных продавцов наборов для рисования

Отличные новости !!! Вы попали в нужное место для рисования набора геометрии.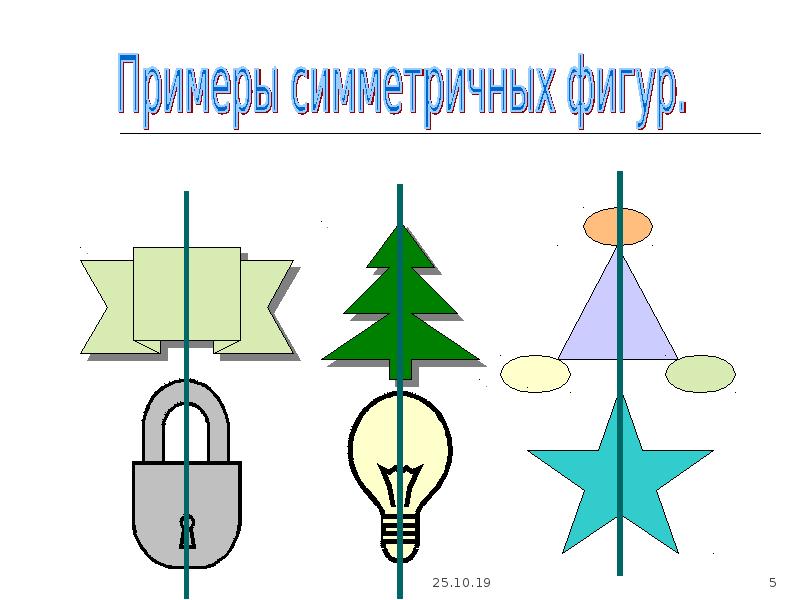 К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress. У нас буквально тысячи отличных продуктов во всех товарных категориях. Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.

Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.

AliExpress никогда не уступит по выбору, качеству и цене. Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны.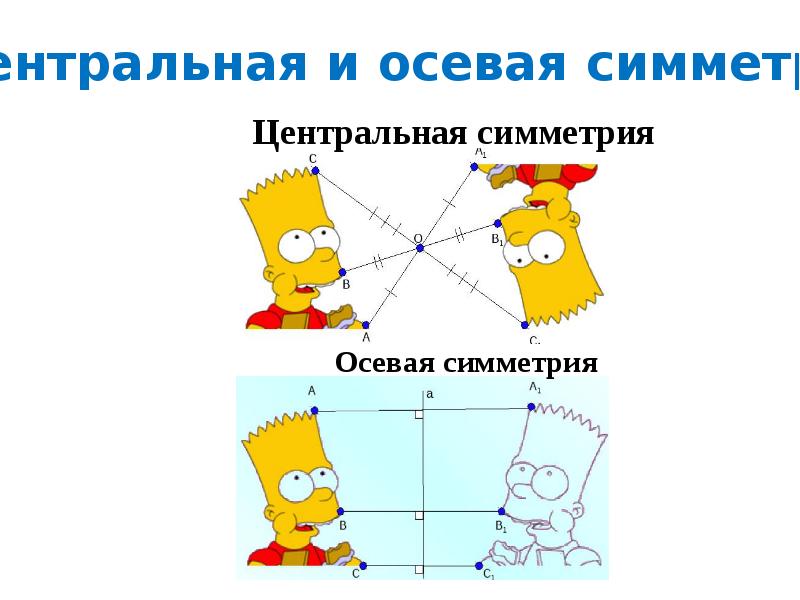 Но вам, возможно, придется действовать быстро, поскольку этот набор геометрии для рисования должен в кратчайшие сроки стать одним из самых востребованных бестселлеров. Подумайте, как вам будут завидовать друзья, когда вы скажете им, что у вас установлена ​​геометрия рисунка на AliExpress.Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете еще больше сэкономить.

Если вы все еще сомневаетесь в выборе геометрического набора и думаете о выборе аналогичного товара, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам разобраться, стоит ли доплачивать за высококачественную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь.А если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. и ожидаемая экономия.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца.Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз. Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.

А если вы новичок на AliExpress, мы откроем вам секрет.Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress. Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, вы сможете приобрести drawing geometry set по самой выгодной цене.

У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы.На AliExpress отличное качество, цена и сервис всегда в стандартной комплектации. Начните самый лучший шоппинг прямо здесь.

Симметрия

— Основы GD&T

Символ GD&T:

Относительно базы : Да

Применимо MMC или LMC: Нет

Обозначение на чертеже:

Описание: 900&T

Симметрия G — это трехмерный допуск, который используется для обеспечения однородности двух элементов детали на базовой плоскости.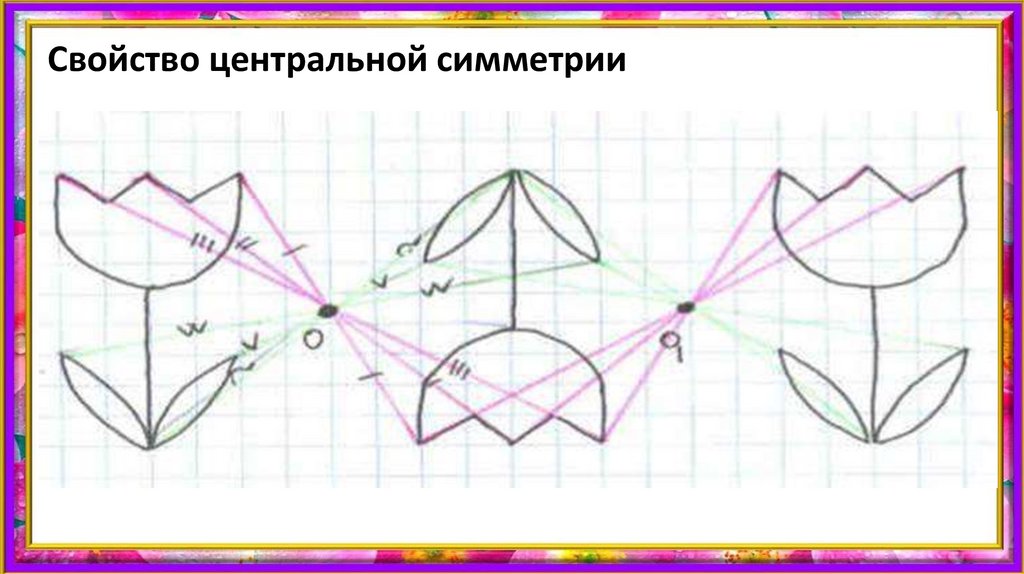 Установленная «истинная» центральная плоскость устанавливается на основе данных, и для того, чтобы симметрия была в пределах допуска, среднее расстояние между каждой точкой на двух поверхностных элементах должно находиться рядом с этой центральной плоскостью. У каждого набора точек на опорных объектах будет средняя точка, которая находится прямо между ними. Если вы возьмете все средние точки всей поверхности, они должны находиться в пределах зоны допуска, чтобы быть в спецификации. Симметрия — не очень распространенная выноска GD&T, поскольку она имеет очень ограниченное функциональное использование (положение центрирования выполняется с помощью Position), а проверка и измерение симметрии могут быть трудными (см. Заключительные примечания).

GD & T Толерантность зона:

параллельных плоскостей на равных сторонах центральной базовой плоскости. Средние точки симметричных поверхностей должны находиться в этой зоне.

Калибровка / Измерение:

Как указывалось ранее, симметрию очень сложно измерить.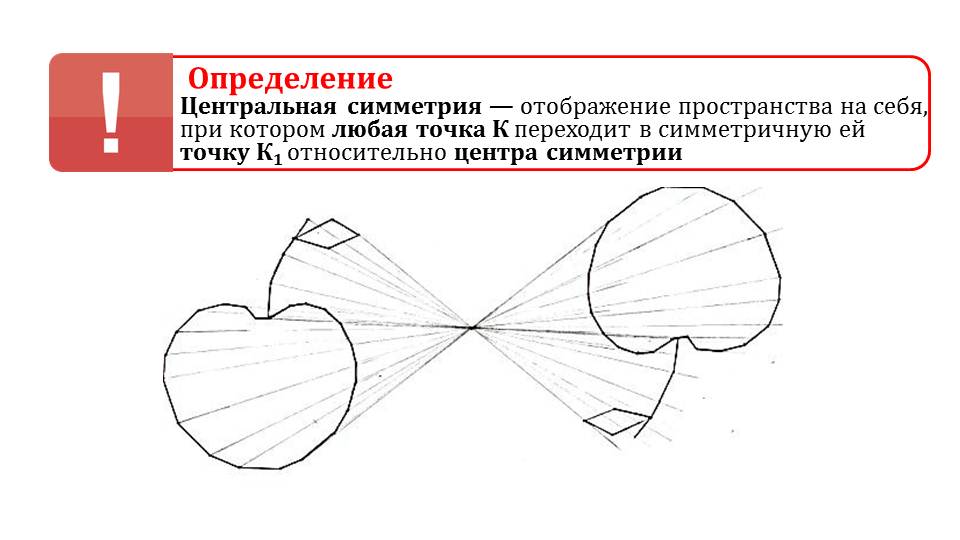 Из-за того, что его зона допуска ограничена виртуальной плоскостью, у вас не может быть датчика, чтобы правильно измерить этот элемент быстро. Обычно для измерения симметрии настраивается КИМ для расчета теоретической базовой плоскости средней точки, измерения поверхностей обеих требуемых поверхностей, а затем определения местоположения средних точек по отношению к базовой плоскости.Это сложный и иногда неточный метод определения симметричности детали.

Связь с другими символами GD&T:

Симметрия — это некруглая версия концентричности. В то время как концентричность действительно является фокусом симметрии относительно базовой оси, символ симметрии фокусируется на симметрии относительно базовой плоскости. Оба символа указывают на то, что теоретическая центральная точка привязки ограничена определенным пределом, чтобы гарантировать однородность всей конструкции.

Когда используется:

Если вы хотите убедиться, что центральная плоскость двух симметричных элементов всегда удерживается точно по центру И имеет ровную форму вдоль поверхности детали. Этот символ может использоваться только для баланса массы и распределения формы. Однако в большинстве случаев лучше избегать использования, так как это очень сложная выноска для измерения и ее легко заменить допуском положения.

Пример:

Если у вас есть вращающийся карданный шарнир, канавка, которая должна всегда иметь равномерный баланс, вам необходимо убедиться, что сопряженная деталь всегда расположена так, чтобы попадать в центр канавки и что форма поверхности должным образом сбалансирована … Вместо того, чтобы расширять канавку, вызывающую ослабление соединения, вы можете ограничить его симметрией.

Пример симметрии 1: обозначьте симметрию, чтобы обеспечить центрирование канавки на средней плоскости блока защелки.

Затем необходимо измерить деталь, чтобы убедиться, что все средние точки сторон блока защелки симметричны относительно центральной оси. Часть должна быть измерена следующим образом:

  1. Меры шириной и расположение обоего сторон опорного блока с помощью базовой точки A (40 мм), а также определить, где точная среднюю плоскость расположена, чтобы установить нашу зону допуска.
  2. Сторона 1 и Сторона 2 детали сканируются на предмет их фактических профилей.
  3. Используя программу, средние точки сканирования Стороны 1 и Стороны 2 накладываются на плоскости виртуальных зон допуска и определяются, находятся ли они в пределах допуска.

Заключительные примечания:

Симметрии следует избегать в большинстве случаев из-за ее особых функциональных требований и сложности измерения. Благодаря плоскостности, параллельности и истинному положению вы можете определить точно такие же ограничения на детали, хотя и требуются дополнительные выноски и измерения.Однако, поскольку истинное положение может быть измерено с помощью датчика (если используется MMC), а плоскостность автоматически контролируется размером и измеряется непосредственно с поверхностей, ими можно управлять в процессе и не требовать своевременных измерений КИМ.

, Томми, 4 ноября 2014 г.

Станьте инженером в своей компании

Изучите GD&T в удобном для вас темпе и с уверенностью примените его в реальном мире.

Comments
Leave Comment