Ромб как правильно нарисовать: Рисунок ромба

---

06.06.2023 Разное

---

Нарисовать ромб из цифр в Python

Вопрос задан 2 года 10 месяцев назад

Изменён 1 год 1 месяц назад

Просмотрен 6k раз

Помогите, пожалуйста, сделать ромб из цифр на Python, уже несколько дней пытаюсь. Должно получаться примерно так:

   1
  121
 12321
  121
   1

Вот мой недоромб, не могу понять, как дописать его правую нижнюю часть:

n = int(input()) 
x = ""
for i in range(1, n + 1): 
    x = x + str(i)
    print(' '*(n-i) + x + x[-2::-1])
    
for i in range(n-1, 0, -1):
    print(' '*(n-i), sep='', end='')
    for k in range(1, i + 1):
        print(k, end='')
    print()   

Заранее спасибо!

• python

4

Не разбирая по четвертям — это не «улитка», которая зависит от сектора.

Тут главное придумать формулу для элемента.

n = 4
w = n*2-1
ar  = [ ]
for y in range(w):
   ar.append([])
   for x in range(w):
       d = n - abs(x+1-n) - abs(y+1-n)
       ar[y].append( d if d > 0 else " ")
for l in ar:
    print(*l,sep='')

def get_list(n):
    return list(range(1, n+1)) + list(range(n-1,0,-1)) # Рисует строку так, как нам нужно
inp = int(input())
height = get_list(inp) # Центральный вертикальный столбец
width = inp*2-1 # Ширина центральной строки. Она берётся как максимальная ширина всего ромба
for step in height: # Идём сверху вниз по вертикальному столбцу
    strs = (str(x) for x in get_list(step)) # И генерируем горизонтальные
    level = ''.join(strs)
    print(level.center(width)) # Правильно выводим строки с учётом максимальной ширины

13

Если все таки «Улитка»

    x= int(input())
    for i in range(1, x + 1):
      print(' '*(x-i), end='')
      for j in range(1, i+1):
        print(j, end = '')
      for j in range(i-1, 0,-1):
        print(j, end = '')
      print()
    for z in range(x-1, 0, -1):
      print(' '*(x-z), end='')
      for k in range(1, z + 1):
        print(k, end='')
      for k in range (z-1,0,-1):
        print (k, end='')
      print()  

1

На первом этапе мы рисуем верхнюю часть ромба, получая ее путем склеивания двух переменных для левой и правой части. На втором этапе от этих переменных и отсекаем по одному символу и продолжаем их склеивать.

ch = 9
sumLeft = ""
sumRight = ""
for i in range(1,ch+1): 
  sumLeft+=str(i)
  print ((" "*(ch-i))+sumLeft + sumRight)
  sumRight = str(i) + sumRight
sumRight = sumRight[1:]
for i in range(ch,1, -1):
  sumLeft = sumLeft[:-1]
  sumRight = sumRight[1:]
  print(" "*(ch+1-i) + sumLeft + sumRight)

1

Простое решение в две строки:

n = int(input())
print('\n'.join(' '*abs(n-i-1)+''.join([str(min(j+1, min(n*2-i-1, i+1)*2-j-1)) 
    for j in range(2*(n-abs(n-i-1))-1)]) for i in range(n*2-1)))

Можно развернуть:

n = int(input())
for i in range(n*2-1):
    print(' '*abs(n-i-1), end='')
    for j in range(2*(n-abs(n-i-1))-1):
        print(min(j+1, min(n*2-i-1, i+1)*2-j-1), end='')
    print()

Верхняя часть кода совпадала с моей, а вот над нижней долго колдовал, да так и не смог ничего родить (я только начал учиться). В итоге смог написать такой вариант (не без помощи добрых людей, конечно):

n = int(input())
for i in range (1, n+1):
    print (' ' * (n-i), *range(1, i+1), *range(i-1, 0, -1), sep='')
for j in range (n, 0, -1):
    print (' ' * (n-j+1), *range(1, j), *range(j-2, 0, -1), sep='')

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

By clicking “Отправить ответ”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.

ромб — Blog — Ghenadie Sontu Fine Art

Изучение и рисование геометрических тел в учебном академическом рисунке является основой для освоения принципов и методов изображения более сложных форм.

Обучение изобразительным искусствам требует строгого соблюдения последовательности усложнения учебных задач и многократных повторений для овладения техникой. Наиболее подходящей формой для усвоения принципов построения рисунка являются геометрические тела, имеющие в своей основе ясные конструктивные строения. На простых геометрических телах легче всего понять и усвоить основы объемно-пространственной конструкции, передачи форм в перспективном сокращении, закономерности светотеней и пропорциональные отношения.

Упражнения по рисованию простых геометрических тел позволяют не отвлекаться на детали, имеющиеся в более сложных формах, таких, как архитектурные объекты и тело человека, а всецело сосредоточиться на главном — изобразительной грамоте.

Правильно понятые и усвоенные закономерности при изображении простых форм должны способствовать более осознанному подходу к рисованию сложных форм в последующем.

Для того чтобы научиться грамотно и правильно изображать форму предмета, необходимо осознать скрытую от глаз внутреннюю структуру предмета — конструкцию. Под словом «конструкция» (от латинского construct) подразумевается «строение», «структура», «план», то есть взаимное расположение частей предмета и их соотношение. Это важно знать и понимать при изображении любых форм. Чем сложнее форма (независимо от материала, фактуры и цвета предмета), тем больше и серьезнее студентам придется изучать внутреннее строение натурной модели. Гак, например, при рисовании живой натуры — головы или фигуры человека, помимо знания общеконструктивных особенностей непременно следует знать и пластическую анатомию. Поэтому без ясного понимания строения формы и характера предмета невозможно грамотно освоить рисунок.

При изображении пространственных форм, кроме знания закономерностей строения конструкции, необходимы знания о законах перспективы, пропорции, светотени. Вопросы, касающиеся перспективы и пропорции, подробно освещены в разделах «Пропорции» и «Основы перспективы».

Для правильного изображения натурной модели студентам необходимо еще раз напомнить о необходимости приучить себя всегда анализировать натуру, ясно представлять ее внешнее и внутреннее строение. К сожалению, как показывает практика, многие студенты ограничиваются лишь поверхностным впечатлением, не углубляясь в суть строения формы предмета. В искусстве, как и в любой науке, к изучению натурного предмета необходимо подходить с научной точки зрения. Подходить к работе следует осознанно, не довольствуясь копированием внешних форм, которые видит глаз. Такое рисование не будет способствовать успешному выполнению работ по изображению как простых, так и сложных форм.

Рисование геометрических форм малоопытным рисовальщикам кажется на первый взгляд достаточно легким. Но это далеко не так. Не имея достаточного опыта в рисовании, студенты легко привыкают к механическому копированию. Поэтому при изображении более сложных форм можно легко запутаться. Для более уверенного овладения рисунком прежде всего необходимо освоить методы анализа форм и принципы геометрического построения простых тел.

Любая форма состоит из плоских фигур: прямоугольников, треугольников, ромбов, трапеций и других многоугольников, которые отграничивают ее от окружающего пространства. Задача заключается в том, чтобы правильно понять, как эти поверхности сочетаются между собой, образуя форму. Для правильного ее изображения студентам необходимо научиться рисовать такие фигуры в перспективе, чтобы без особого труда выделять на плоскости объемные тела, ограниченные этими плоскими фигурами. Плоские геометрические фигуры служат основой понимания конструктивного построения объемных тел. Так, например, квадрат дает представление о построении куба, прямоугольник — о построении призмы параллелепипеда, треугольник — пирамиды, трапеция — усеченного конуса, круг представляется шаром, цилиндром и конусом, а эллипсовидные фигуры — шарообразными (яйцевидными) формами (рис. 34).

Все предметы имеют объемно-пространственные характеристики: высоту, длину и ширину. Для определения и изображения их на плоскости пользуются точками и линиями. Точками определяются характерные узлы конструкции предметов, ими устанавливается взаимное пространственное расположение узлов, характеризующее конструкцию формы в целом.

Линия является одним из основных изобразительных средств. Линиями обозначают контуры предметов, образующие их форму. Ими обозначают высоту, длину, ширину, конструктивные оси, вспомогательные, определяющие пространства линии, линии построения и многое другое.

Для основательного изучения геометрические формы лучше всего следует рассматривать в виде прозрачных каркасных моделей. Это позволяет лучше проследить, понять и усвоить основы пространственного построения конструкций и перспективного сокращения форм геометрических тел: куба, пирамиды, цилиндра, шара, конуса и призмы. Вместе с тем, такой прием в значительной степени облегчает построение рисунка, в котором отчетливо прослеживаются все пространственные углы, ребра, грани тела, независимо от их поворотов в пространстве и в перспективном сокращении. Каркасные модели позволяют развить у студентов объемно-пространственное мышление, тем самым способствуя правильному изображению геометрической формы на плоскости бумаги.

Для основательного закрепления в сознании студентов объемно-пространственного представления о строении этих форм было бы наиболее эффективным выполнить их своими руками. Модели можно сделать без особого труда из подручных материалов: обыкновенной гибкой алюминиевой, медной или любой другой проволоки, деревянных или пластмассовых реек. В последующем, в целях усвоения закономерностей светотени, можно будет изготовить модели из бумаги или тонкого картона. Для этого необходимо сделать заготовки — соответствующие развертки или отдельно вырезанные плоскости для склеивания. Не менее важен сам процесс моделирования, который больше принесет пользы для осознания обучающимися сущности строения той или иной формы, чем использование уже готовой модели. Для изготовления каркасных и бумажных моделей потребуется немало времени, поэтому в целях его экономии не следует делать модели большого размера — достаточно, если их габариты не будут превышать трех, четырех или пяти сантиметров.

Поворачивая изготовленную бумажную модель под разными углами к источнику света, можно проследить за закономерностями света и тени. При этом следует обратить внимание на изменение пропорциональных отношений частей предмета, а также на перспективное сокращение форм. Приближая и отдаляя модель от источника света, можно увидеть, как меняется контрастность освещения на предмете. Так, например, при приближении к источнику света свет и тень на форме приобретают наибольшую контрастность, а по мере удаления становятся менее контрастными. Причем, близлежащие углы и грани будут наиболее контрастными, а углы и грани, находящиеся в пространственной глубине,

— менее контрастными. Но самое главное на начальном этапе рисования
— это умение правильно отображать объемно-пространственную конструкцию форм с помощью точек и линий на плоскости. Это является основополагающим принципом в освоении рисунка простых геометрических форм, а также при последующем изучении более сложных форм и осознанном их изображении.

Для последовательного изучения, анализа форм и выполнения рисунка геометрических тел следует рассмотреть приемы и принципы их построения на плоскости.

В целях соблюдения последовательности в работе над рисунком, основанной на принципе «от простого к сложному», необходимо вначале изучить простые геометрические тела: куб, призму, пирамиду, цилиндр.

Ромб — свойства, определение, формулы, примеры

Ромб — замкнутая двумерная плоская фигура. Он считается особым параллелограммом, и благодаря своим уникальным свойствам он приобретает индивидуальную идентичность четырехугольника. Ромб также называют равносторонним четырехугольником, так как все его стороны равны по длине. Термин «ромб» произошел от древнегреческого слова «ромбос», что на самом деле означает что-то вращающееся. Давайте узнаем больше о ромбе и его свойствах в этой статье.

1.	Что такое ромб?
2.	Свойства ромба
3.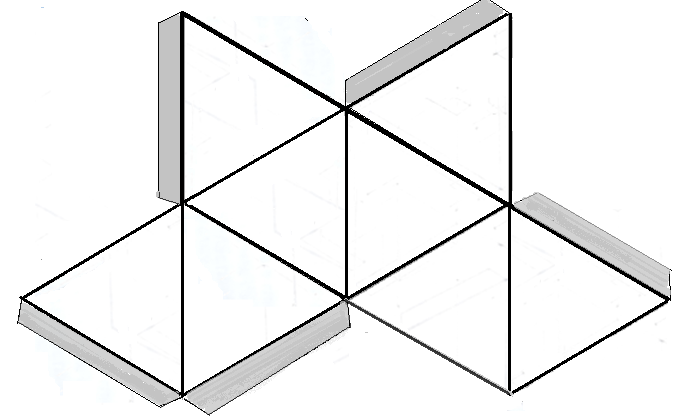	Как выглядит ромб?
4.	Формулы ромба
5.	Часто задаваемые вопросы о Rhombus

Что такое ромб?

Ромб можно определить как специальный параллелограмм , поскольку он удовлетворяет требованиям параллелограмма, то есть четырехугольника с двумя парами параллельных сторон. Кроме того, у ромба все четыре стороны равны, как у квадрата. Вот почему он также известен как наклонный квадрат. Посмотрите на изображение ниже, чтобы понять взаимосвязь формы ромба с параллелограммом и квадратом.

На приведенном выше рисунке мы можем заметить, что каждый ромб, который мы видим, также будет параллелограммом, но не каждый параллелограмм является ромбом. Квадрат можно рассматривать как частный случай ромба, поскольку он имеет четыре равные стороны. Все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми . И, следовательно, ромб с прямыми углами можно считать квадратом.

Отсюда можно сделать вывод, что:

• Все ромбы или ромбы являются параллелограммами, но не все параллелограммы являются ромбами.
• Все ромбы или ромбы не являются квадратами, но все квадраты являются ромбами.

Ромб может иметь три дополнительных имени:

• Ромб
• Пастилка
• Ромб

Свойства ромба

Ромб считается одним из особых параллелограммов, так как обладает всеми свойствами параллелограмма. Две диагонали ромба являются его двумя линиями симметрии. Ось симметрии можно рассматривать как линию, которая делит объект на две равные половины. Он создает зеркальное отражение обеих сторон объекта. Говорят, что ромб обладает симметрией отражения по обеим диагоналям. Общие свойства параллелограмма следующие:

• Противоположные углы равны или равны.
• Противоположные стороны равны и параллельны.
• Диагонали делят друг друга пополам.
• Сумма любых двух соседних или следующих друг за другом углов равна 180°.

Ромб, как и все геометрические фигуры, обладает уникальными свойствами. В таблице ниже описаны свойства ромба.

Свойства ромба	Артикул
Все стороны ромба конгруэнтны (равны).	Здесь AB = CD = DA = BC
Диагонали делят друг друга пополам под углом 90°, или мы также можем сказать, что каждая из двух диагоналей ромба является серединным перпендикуляром к другой.	Здесь диагонали DB и CA делят друг друга пополам под углом 90°
Противоположные углы равны, а противоположные стороны параллельны.	Здесь, компакт-диск || АВ и ВС || ОБЪЯВЛЕНИЕ. ∠А = ∠С и ∠D = ∠В
Смежные углы в сумме дают 180°	∠А + ∠В = 180° ∠В + ∠С = 180° ∠C + ∠D = 180° ∠А + ∠D = 180°

Одна вещь, которую мы должны помнить о диагонали ромба, заключается в том, что в дополнение к разделению пополам под углом 90 ° две диагонали, разделенные пополам, будут иметь одинаковую длину. Например: если длина диагонали равна 10 см, а другая диагональ делит ее пополам, то она делится на два отрезка по 5 см. Если знать сторону ромба и величину некоторых углов, то можно определить длину диагонали.

Как выглядит ромб?

Ромб – это четырехугольник в форме ромба, у которого все четыре стороны равны. Мы можем видеть фигуры в форме ромба в нашей повседневной жизни. Некоторые из реальных примеров ромба показаны на рисунке ниже: бриллиант, воздушный змей, серьга и т. д.

Формулы ромба

Формулы для ромбов определены для двух атрибутов:

1. Площадь ромба, A = 1/2 × d ₁ × d ₂ , где d ₁ и d ₂ — диагонали ромба.
2. Периметр ромба, P = 4 × a, где a — сторона.

Площадь и периметр ромба

Площадь ромба можно определить как количество пространства, заключенного или охваченного ромбом в двухмерной плоскости. Это половина произведения длин диагоналей. Итак, A = 1/2 × d ₁ × d ₂ , где d ₁ и d ₂ — длины диагоналей.

Так же, как и у квадрата, все четыре стороны ромба равны, значит, формула периметра ромба есть произведение длины одной стороны на 4. Получаем P = (4 × a) единиц , где а — сторона ромба.

☛ Важные примечания о ромбе

Вот список нескольких моментов, которые следует помнить при изучении ромба:

• Смежные углы в ромбе смежные, в сумме они составляют 180°.
• Диагонали делят друг друга пополам под прямым углом.
• Все квадраты — ромбы, но не все ромбы — квадраты.

☛ Похожие темы:

Ознакомьтесь с этими интересными статьями, чтобы узнать больше о ромбе и связанных с ним темах.

• Калькулятор площади ромба
• Рабочие листы с ромбами
• Разница между воздушным змеем и ромбом

Cuemath — одна из ведущих в мире платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Ромб Примеры

1. Пример 1: Давид начертил ромб, длины двух диагоналей d ₁ и d ₂ равны 5 единицам и 10 единицам соответственно. Он просит свою сестру Линду помочь ему найти этот район. Поможешь Линде найти ответ?

   Решение:

   Дано:

   Диагональ, d ₁ = 5 единиц, а d ₂ = 10 единиц

   A = (d ₁ × d ₂ )/2

   A = (5×10)/2

   A = 25 кв. ед.

   Ответ: Площадь ромба = 25 кв. ед.

2. Пример 2: Эльзе дали площадь ромба, равную 100 квадратным единицам, и длину одной диагонали, равную 20 единицам. Поможешь Эльзе найти длину другой диагонали?

   Решение:

   Дано:

   Площадь = 100 кв. единиц и диагональ d ₁ = 20 шт. 4 2 = 10 единиц

   Ответ: Длина другой диагонали равна 10 единицам.

3. Пример 3: Сэм и Виктор играли в классики и заметили на детской площадке плитку в форме ромба. Длина каждой стороны плитки равнялась 15 единицам. Поможешь Сэму и Виктору найти периметр плитки?

   Решение:

   Дано:

   Длина плитки = 15 единиц.

   Поскольку все стороны ромба равны, все четыре стороны равны 15 единицам.

   Периметр = 4 × сторона = 4 × 15 = 60 единиц

   Ответ: Периметр плитки = 60 единиц.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по ромбу

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о Rhombus

Что такое ромб в геометрии?

Ромб — это двумерная фигура с четырьмя сторонами, поэтому ее называют четырехугольником. Он имеет две диагонали, которые делят друг друга пополам под прямым углом. У него также параллельны противоположные стороны, а сумма всех четырех внутренних углов равна 360 градусам.

Все ли квадраты ромбы?

Да, все квадраты — ромбы. Квадрат можно рассматривать как частный случай ромба, поскольку он имеет четыре стороны одинаковой длины. Все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми. Следовательно, ромб с прямыми углами можно считать квадратом.

Какой формы ромб?

Ромб – четырехугольник в форме ромба. Если вы посмотрите на колоду карт и вытащите 13 ромбовидных карт, вы обнаружите, что геометрическая форма ромба — это ромб. У него все четыре стороны равны, а противоположные стороны параллельны друг другу. Он выглядит как наклонный квадрат.

Является ли ромб правильным многоугольником?

Нет, ромб не является правильным многоугольником. Правильный многоугольник должен быть равноугольным (все его углы имеют одинаковую меру) и конгруэнтным или равносторонним (все его стороны имеют одинаковую длину). Но ромб только равносторонний: все его стороны имеют одинаковую длину и только противоположные углы равны. Ромб никогда нельзя считать правильным многоугольником, так как это всего лишь равносторонний многоугольник, а не равноугольный многоугольник.

Какова площадь ромба?

Площадь ромба рассчитывается путем деления произведения диагоналей на 2. Математически это можно определить как: \(A = \frac{{d_1 d_2}}{2}\), где d ₁ d ₂ — диагонали ромба.

Каковы четыре свойства ромба?

Ромб – это четырехугольник, обладающий следующими четырьмя свойствами:

• Противоположные углы всегда равны.
• Все стороны равны, а противоположные стороны параллельны друг другу.
• Диагонали делят друг друга пополам под углом 90 градусов и имеют одинаковую длину.
• Сумма любых двух смежных углов всегда будет равна 180°.

В чем разница между ромбом и квадратом?

Основное отличие ромба от квадрата в том, что углы ромба не равны 90°, тогда как все углы квадрата равны 90°. Часто говорят, что квадрат — это ромб, но ромб — это не всегда квадрат.

В чем разница между параллелограммом и ромбом?

Отличие параллелограмма от ромба в том, что у ромба все четыре стороны равны по размеру, тогда как у параллелограмма противоположные стороны равны.

Какие основные формулы ромба?

Несколько основных формул ромба приведены ниже:

• Площадь ромба = 1/2 × d ₁ × d ₂ квадратных единиц.
• Периметр ромба = (4 × стороны) единиц.

Чему равна сумма внутренних углов ромба?

Сумма внутренних углов ромба равна 360°.

Все ли углы ромба равны 90°?

Нет, углы ромба не обязательно должны быть прямыми. Ромб, у которого все четыре внутренних угла равны 90 градусам, считается квадратом.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по ромбу

Ответ: Рисунок MNPQ — ромб. Ничья…

P Предварительные понятия1 Отношения линий и углов2 Параллельные прямые3 Треугольники4 Четырехугольники5 Подобные треугольники6 Окружности7 Геометрическое место и совпадение8 Площади многоугольников и окружностей9 Поверхности и тела10 Аналитическая геометрия11 Введение в тригонометриюA Приложение expand_more

1. 1 Ранние определения и постулаты1 .2 Углы и их отношения 1.3 Введение в геометрическое доказательство1.4 Отношения: перпендикулярные линии1.5 Формат Доказательство теоремы1.CR Повторные упражнения1.CT Test expand_more

Задача 1CR. Назовите четыре компонента математической системы. Задача 2CR. Назовите три типа рассуждений. Задача 3CR. Назовите четыре характеристики хорошего определения. Задача 4CR. проиллюстрирован тип рассуждений. Наблюдая, как кувшин разогревается… Задача 5CR: В повторных упражнениях с 4 по 6 назовите показанный тип рассуждений. Лора уехала в лагерь. О… Задаче 6CR: В повторных упражнениях с 4 по 6 назовите проиллюстрированный тип рассуждения. Сара знает правило Число… Задача 7CR: В повторных упражнениях 7 и 8 сформулируйте гипотезу и вывод для каждого утверждения. Если… Проблема 8CR: В обзорных упражнениях 7 и 8 сформулируйте гипотезу и вывод для каждого утверждения. Диагонали… Задача 9CRЗадача 10CRЗадача 11CRЗадача 12CR: A, B и C — три точки на прямой. АС=8, ВС=4 и АВ=12. Какая точка должна быть между другой… Задача 13CRЗадача 14CR: Фигура MNPQ — ромб. Проведите диагонали MP и QN ромба. Как выглядят MP и QN… Задача 15CR: В повторных упражнениях с 15 по 17 нарисуйте и подпишите описанные фигуры. Точки A, B, C и D… Задача 16CR: В повторении упражнений с 15 по 17 нарисуйте и подпишите описанные фигуры. Прямая l пересекает плоскость X в точке… Задача 17CR: В повторении упражнений с 15 по 17 нарисуйте и подпишите описанные фигуры. Плоскость M содержит пересекающиеся… Задача 18CR: Судя по внешнему виду, какой тип угла показан? Задача 19CR: Основываясь на внешнем виде, какой тип угла показан? Задача 20CR: Дано: BD делит ABC пополам mABD=2x+15 mDBC=3x+5 Найти: mABCЗадача 21CR: Дано: mABD=2x+5 mDBC=3×4 mABC= 86 Найти: mDBCPProblem 22CR: Дано: AM=3×1 MB=4×5 M — середина AB Найти: ABProblem 23CR: Дано: AM=4×4 MB=5x+2 AB=25 Найти: MBProblem 24CR: Дано: D — середина AC ACBC CD=2x+5 BC=x+28 Найти: ACProblem 25CR: Дано: m3=7×21 m4=3x+7 Найти: mFMHProblem 26CR: Дано: mFMH=4x+1 m4=x+4 Найти: m4Problem 27CR: In по фигуре найдите: a KHFJ b MJMH c KMJJMH d MKMH Задача 28CR: Дано: EFG — прямой угол. mHFG=2×6 mEFH=3mHFG Находка: mEFHЗадача 29ЧР: Два угла являются дополнительными. Один угол в 40 раз больше другого. Найдите меры… Задача 30CR: a Напишите выражение для периметра показанного треугольника. ПОДСКАЗКА: сложите длины сторон… Задача 31CR: Сумма мер всех трех углов треугольника в обзорном упражнении 30 равна 180. Если сумма… Задача 32CR: Сьюзан хочет получить 4- ft доска с некоторыми колышками на нем. Она хочет оставить 6 дюймов на каждом конце и 4… Задача 33CR. Укажите, всегда ли предложения в повторных упражнениях с 33 по 37 истинны A, иногда истинны S, или… Задача 34CR. Укажите, являются ли предложения в повторении Упражнения с 33 по 37 всегда верны A, иногда истинны S или… Задача 35CR. Укажите, всегда ли предложения в повторных упражнениях 33–37 истинны A, иногда истинны S или… Задача 36CR. в упражнениях на повторение с 33 по 37 всегда верно A, иногда верно S или… Задача 37CR. Укажите, всегда ли предложения в упражнениях на повторение 33-37 верны A, иногда верно S или.