Рисунок симметрии: Осевая симметрия одна рисунок сложный. Как нарисовать симметричный предмет

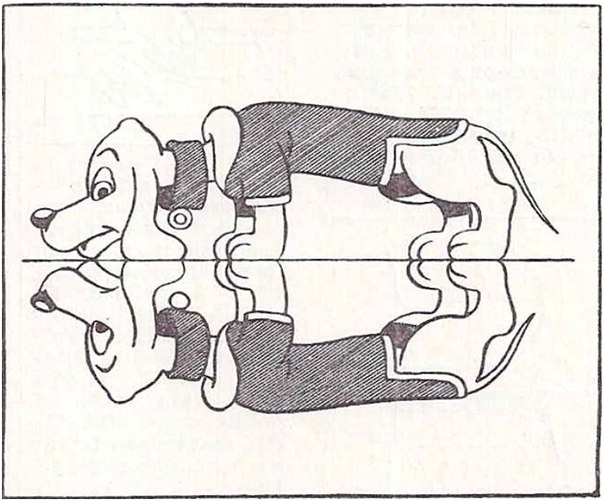
Ход урока:

На прошлом занятии мы с вами проходили тему “Центральная и осевая симметрия”, повторим некоторые изученные понятия.

— Что означает слово “симметрия”?

(Одинаковость в расположении, красота, пропорциональность, гармония…)

— С какими видами симметрии мы познакомились?

(Осевая, центральная, зеркальная)

— Выберите из предложенных вам рисунков, которые нарисовали учащиеся вашего класса, те, на которых имеется центральная симметрия, и те, на которых изображена осевая симметрия (рисунок 1), (рисунок 2), (рисунок 3), (рисунок 4).

— Изображение на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно стебля. С симметрией мы часто встречаемся и архитектуре, технике, быту и в искусстве. Сегодня мы остановимся на симметрии в суконной аппликации и мозаике народов Якутии.

О геометрических представлениях и знаниях якутов нам расскажет ученик нашего класса. Сообщение учащегося.

Геометрической фигурой называется всякое непустое множество точек. Значит: точка, отрезок, луч, прямая, кривая, треугольник, куб, пирамида, конус и др., — геометрические фигуры. Имели ли якуты представления о них? Да. О геометрических знаниях свидетельствуют жилища, хозяйственные постройки, ювелирные изделия, посуда и традиционные орудия труда. Берестяные летние жилища якутов всегда были конической формы – ураса. Более сложную форму имеет якутская юрта, которая состоит из объединения четырехугольной усеченной и треугольной пирамид (рисунок 5).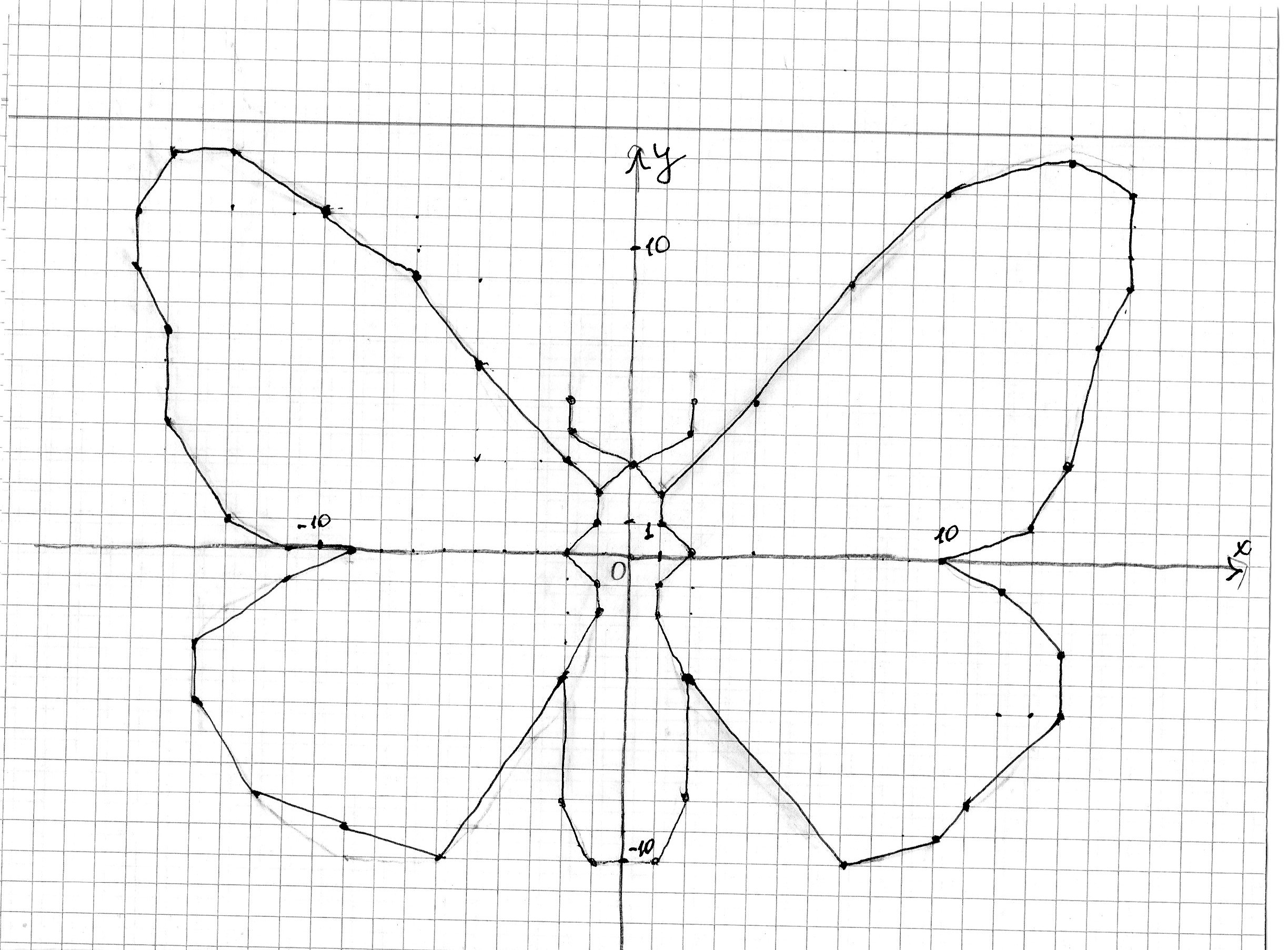

Вершина якутского стиля – изготовление сосудов из дерева. Многие ученые этнографы отмечали, что по плавности и “музыкальности” контуров, ясности пропорций чороны выдерживают сравнение с античными сосудами (рисунок 6). Для каждой части чорона существует определенная группа орнаментов: в виде треугольников, точек, гребешков, ячеек сети, зигзагов и ромбов.

Широкое распространение среди якутов издревле получили суконная аппликация и меховая мозаика. В ней преобладают геометрические фигуры: треугольник, квадрат, прямоугольник, ромб, трапеция и другое.

Когда якутские женщины украшают коврики, рукавицы, чепраки, пальто и другую одежду, опираясь на интуитивные геометрические представления о центральной и осевой симметрии, о повороте и параллельном переносе, т.е. о геометрических преобразованиях, основываясь на практических знаниях о свойствах геометрических фигур.

Таким образом, геометрические знания и представления якутов составляют богатую народную мудрость и передаются из поколения в поколения, тем самым способствуя творцам материальной и духовной культуры получать мировое признание.

— А теперь вашему вниманию представляется несколько фотографий из альбома-монографии Анны Зверевой, известной мастерицы, прикладника и дизайнера.

-Наглядным примером центральной и осевой симметрии является ее триптих “Ленский лес”.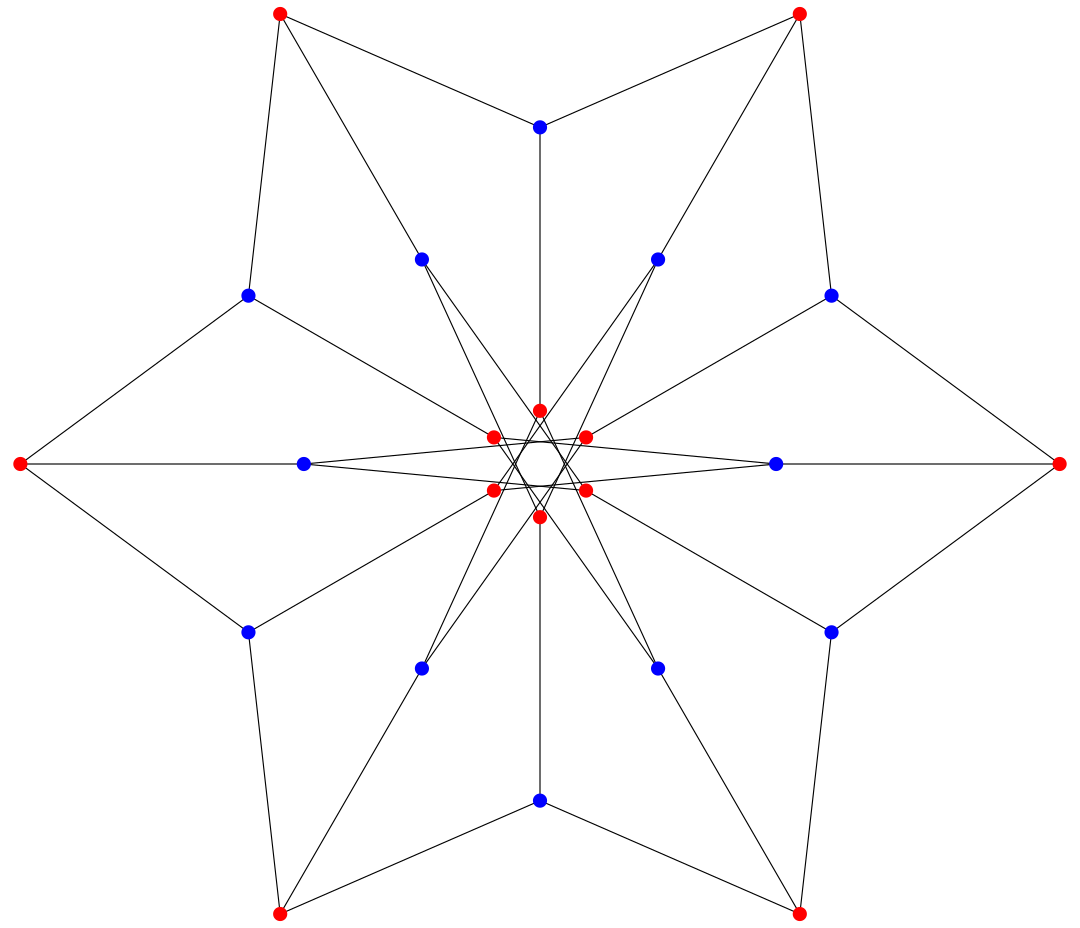 Рассмотрим один из его элементов (Рисунок7).

— Из каких фигур состоит данный элемент? (Квадрат, ромб, прямоугольник, треугольник).

— Каким типом симметрии пользовался мастер при его создании?

Цель нашего занятия: познакомиться с разнообразными симметричными орнаментами в суконной аппликации якутских мастеров и научится составлять их.

Работа с образцами (рисунок 8).

-Какие геометрические фигуры использованы для составления данных орнаментов?

-Как расположены геометрические фигуры? (В определенном порядке).

-Какой тип симметрии использован в каждом образце?

-Как можно назвать такой порядок в изображении? (Узор).

-А повтор узора называется ритмом.

Важно помнить, что геометрические фигуры в орнаменте располагаются строго по линиям симметрии, либо центрально симметричны.

-Мы сегодня будем конструировать орнамент оберега “биэсхарах” (рисунок 9). У якутов это символ предупреждения опасности, защита от злых духов. Его носят на шее, подвешенном на тоненьком кожаном ремешке. Он состоит: во внешнем поле выполнена аппликация из цветных суконных лоскутков размером с ноготь.

Работа с конструктором

Составление орнаментов — настоящее искусство. Им в совершенстве владеют архитекторы, дизайнеры и строители. Сегодня и мы поучимся их составлять.

(Класс делится на два варианта, каждому варианту дается карточка-инструктор построения орнамента оберега).

Конструктор 1 (рисунок10) дается первому варианту.

Конструктор 2 (рисунок 11) дается второму вариант.

Цвет очень много значит для народов Якутии. Данный оберег содержит цвета: кирпично-красный, символизирующий силу и красоту, черный это символ плодородия земли, зеленый – символ мира, зеленеющей долины и белый цвет – символ чистоты помыслов, белизны снежного покрова.

Оценка выполнения работы по карточкам.

-Сегодня мы прикоснулись к творчеству мастеров земли, на которой живем. А также еще раз усовершенствовали свои навыки построения симметричных фигур.

Психологи замечают, что такого рода занятия успокаивают нервы и способствуют появлению внутренней гармонии. Желаю вам взять на вооружение данные вам на уроке знания и умения, чтобы стать более развитыми и гармоничными личностями.

Дома раскрасьте свой оберег в те цвета, которые вам больше нравятся и объясните, почему.

1. Т. М. Амосова “Математические знания и представления якутов” ЯНКИ “Бичик” 1994 г.
2. Б. Ф. Неустроев “” Узоры шитья” “Бичик” 2002 г.
3. А. А. Иванов “” Якутские узоры” “Бичик” 1990 г.
4. А. Н Зверева (альбом — монография) ОНО “Иван Федоров” С – П 2000 г.

Симметрия и её виды | Обучонок

1. Симметрия и ее виды

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека. И употреблялось скульпторами ещё в 5 веке до нашей эры. Слово “симметрия” греческое, оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”.



Его широко используют все без исключения направления современной науки. Немецкий математик Герман Вейль сказал: “Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века.

1.1. Осевая симметрия

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (Рисунок 2.1). Каждая точка прямой а считается симметричной самой себе.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой a также принадлежит этой фигуре (Рисунок 2.2).

Прямая а называется осью симметрии фигуры.

Говорят также, что фигура обладает осевой симметрией.

Осевой симметрией обладают такие геометрические фигуры как угол, равнобедренный треугольник, прямоугольник, ромб (Рисунок 2.3).

Фигура может иметь не одну ось симметрии. У прямоугольника их две, у квадрата – четыре, у равностороннего треугольника – три, у круга – любая прямая, проходящая через его центр.

Если присмотреться к буквам алфавита (Рисунок 2.4)., то и среди них можно найти, имеющие горизонтальную или вертикальную, а иногда и обе оси симметрии. Объекты, имеющие оси симметрии достаточно часто встречаются в живой и неживой природе.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

В своей деятельности человек создаёт много объектов (в том числе и орнаменты), имеющих несколько осей симметрии.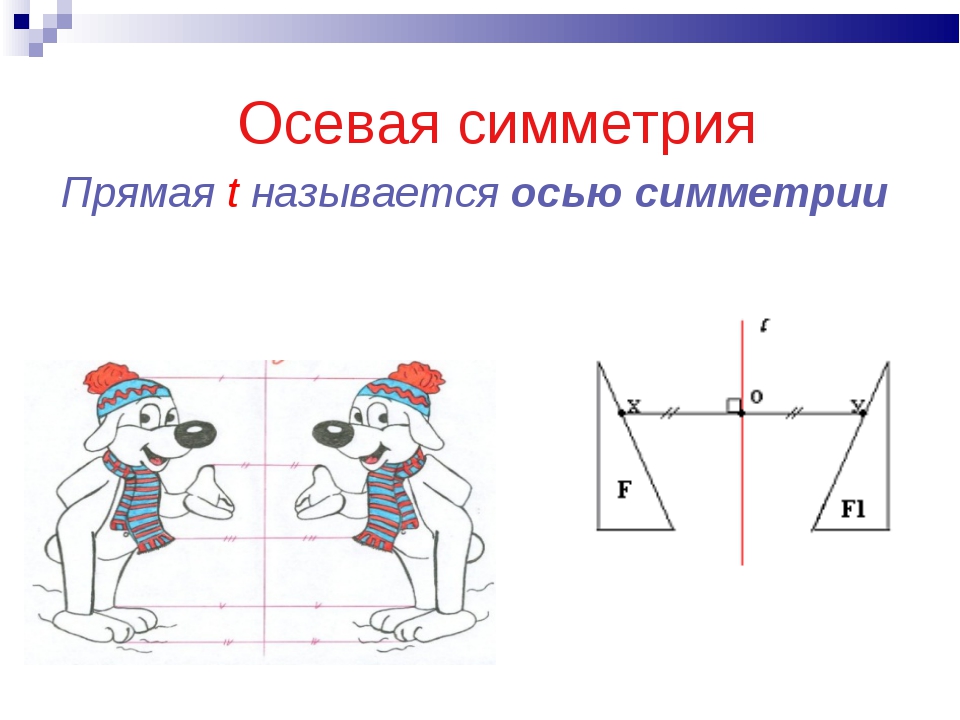

1.2 Центральная симметрия


Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1. Точка О считается симметричной самой себе (Рисунок 2.5).

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре [1].

Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм (Рисунок 2.6).

Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей.

Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии у прямой их бесконечно много — любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.

1.3. Поворотная симметрия

Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.

Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой.

Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».

На рисунке 2.7. даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го. [3]


Перейти к разделу: 1.4. Зеркальная симметрия

10 превосходных примеров симметрии в природе

На протяжении веков симметрия остается предметом, который очаровывает философов, астрономов, математиков, художников, архитекторов и физиков. Древние греки были совершенно одержимы ею – и даже сегодня мы, как правило, сталкиваемся с симметрией во всем от расположения мебели до стрижки волос.

Просто имейте в виду: как только вы осознаете это, вы, вероятно, испытаете непреодолимое желание искать симметрию во всем, что видите.

Брокколи романеско

Возможно увидев брокколи романеско в магазине, вы подумали, что это ещё один образец генномодифицированного продукта. Но на самом деле это ещё один пример фрактальной симметрии природы. Каждое соцветие брокколи имеет рисунок логарифмической спирали. Романеско внешне похожа на брокколи, а по вкусу и консистенции – на цветную капусту. Она богата каротиноидами, а также витаминами С и К, что делает её не только красивой, но и здоровой пищей.

Соты

На протяжении тысяч лет люди удивлялись идеальной гексагональной форме сот и спрашивали себя, как пчелы могут инстинктивно создать форму, которую люди могут воспроизвести только с помощью циркуля и линейки. Как и почему пчелы имеют страстное желание создавать шестиугольники? Математики считают, что это идеальная форма, которая позволяет им хранить максимально возможное количество меда, используя минимальное количество воска. В любом случае, все это продукт природы, и это чертовски впечатляет.

Подсолнухи

Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии, известной как последовательность Фибоначчи. Последовательность Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. (каждое число определяется суммой двух предыдущих чисел). Если бы мы не спешили и подсчитали количество семян в подсолнухе, то мы бы обнаружили, что количество спиралей растет по принципам последовательности Фибоначчи. В природе есть очень много растений (в том числе и брокколи романеско), лепестки, семена и листья которых отвечают этой последовательности, поэтому так трудно найти клевер с четырьмя листочками.

Но почему подсолнечник и другие растения соблюдают математические правила? Как и шестиугольники в улье, все это – вопрос эффективности.

Раковина Наутилуса

Помимо растений, некоторые животные, например Наутилус, отвечают последовательности Фибоначчи. Раковина Наутилуса закручивается в «спираль Фибоначчи». Раковина пытается поддерживать одну и ту же пропорциональную форму, что позволяет ей сохранять её на протяжении всей жизни (в отличие от людей, которые меняют пропорции на протяжении жизни). Не все Наутилусы имеют раковину, выстроенную по правилам Фибоначчи, но все они отвечают логарифмической спирали.

Прежде, чем вы позавидуете моллюскам-математикам, вспомните, что они не делают этого специально, просто такая форма наиболее рациональна для них.

Животные

Большинство животных имеют двустороннюю симметрию, что означает, что они могут быть разделены на две одинаковых половинки. Даже люди обладают двусторонней симметрией, и некоторые ученые полагают, что симметрия человека является наиболее важным фактором, который влияет на восприятие нашей красоты. Другими словами, если у вас однобокое лицо, то остается надеяться, что это компенсируется другими хорошими качествами.

Некоторые доходят до полной симметрии в стремлении привлечь партнера, например павлин. Дарвин был положительно раздражен этой птицей, и написал в письме, что «Вид перьев в хвосте павлина, всякий раз, когда я смотрю на него, делает меня больным!» Дарвину, хвост казался обременительным и не имеющим эволюционного смысла, так как он не соответствовал его теории «выживания наиболее приспособленных». Он был в ярости, пока не придумал теорию полового отбора, которая утверждает, что животные развивают определенные функции, чтобы увеличить свои шансы на спаривание. Поэтому павлины имеют различные приспособления для привлечения партнерши.

Паутина

Есть около 5000 типов пауков, и все они создают почти идеальное круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.

Круги на полях

Дайте паре обманщиков доску, косилки и спасительную темноту, и вы увидите, что люди тоже создают симметричные формы. Из-за того, что круги на полях отличаются сложностью дизайна и невероятной симметрией, даже после того, как создатели кругов признались и продемонстрировали свое мастерство, многие люди до сих пор верят, что это сделали космические пришельцы.

По мере усложнения кругов все больше проясняется их искусственное происхождение. Нелогично предполагать, что пришельцы будут делать свои сообщения все более трудными, когда мы не смогли расшифровать даже первые из них.

Независимо от того, как они появились, круги на полях приятно рассматривать, главным образом потому, что их геометрия впечатляет.

Снежинки

Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.

Галактика Млечный Путь

Как мы уже видели, симметрия и математические модели существуют почти везде, но разве эти законы природы ограничиваются нашей планетой? Очевидно, нет. Недавно открыли новую секцию на краю Галактики Млечного Пути, и астрономы считают, что галактика представляет собой почти идеальное зеркальное отражение себя.

Симметрия Солнца-Луны

Если учесть, что Солнце имеет диаметр 1,4 млн. км, а Луна – 3474 км, кажется почти невозможным то, что Луна может блокировать солнечный свет и обеспечивать нам около пяти солнечных затмений каждые два года. Как это получается? Так совпало, что наряду с тем, что ширина Солнца примерно в 400 раз больше, чем Луна, Солнце также в 400 раз дальше. Симметрия обеспечивает то, что Солнце и Луна получаются одного размера, если смотреть с Земли, и поэтому Луна может закрыть Солнце. Конечно, расстояние от Земли до Солнца может увеличиваться, поэтому иногда мы видим кольцевые и неполные затмения. Но каждые один-два года происходит точное выравнивание, и мы становимся свидетелями захватывающих событий, известных как полное солнечное затмение. Астрономы не знают, как часто встречается такая симметрия среди других планет, но они думают, что это довольно редкое явление. Тем не менее, мы не должны предполагать, что мы особенные, так как все это дело случая. Например, каждый год Луна отдаляется примерно на 4 см от Земли, это означает, что миллиарды лет назад каждое солнечное затмение было бы полным затмением. Если и дальше все пойдет так, то полные затмения, в конце концов, исчезнут, и это будет сопровождаться исчезновением кольцевых затмений. Получается, что мы просто находимся в нужном месте в нужное время, чтобы увидеть это явление.

Смотрите также выпуск – Психоделические картины, созданные наукой, Фрактальные узоры на поверхности Земли

А вы знали, что у нас есть Instagram и Telegram?

Подписывайтесь, если вы ценитель красивых фото и интересных историй!

Факультативное занятие «Осевая симметрия в северных узорах» – УчМет


Попова Валентина Николаевна
учитель математики
1 квалификационная категория
Архангельская область Шенкурский район с. Ровдино
МБОУ «Ровдинская СОШ»
математика, факультатив «Наглядно — практическая геометрия».
тема «Осевая симметрия в северных узорах».
6 класс
продолжительность урока: 45 минут
Занятие факультативного курса
«Наглядно-практическая геометрия» в 6 классе
по теме «Осевая симметрия в северных узорах»
Тема «Симметрия на плоскости и в пространстве» является благодатной темой в плане эстетического воспитания обучающихся в процессе обучения математике.
Более узкая тема «Осевая симметрия в северных узорах» дает возможность установления межпредметных связей математики с изобразительным искусством, технологией; использования регионального компонента на уровне знаний и умений обучающихся 6 класса.
Цели занятия
— образовательная: закрепить основные понятия по теме «осевая симметрия», отработать навыки построения симметричных фигур, нахождения осей симметрии на рисунке;
— воспитательные: формировать интерес к истории и традициям родного края;
— развивающие: способствовать формированию у учащихся умения сравнивать, выделять главное, применять знания в различных ситуациях.
Оборудование и наглядность:
1. Компьютер, проектор, экран;
2. Предметы быта северной деревни (старинные и наших дней): посуда, прялки, полотенца, салфетки, лоскутные покрывала, туеса;
3. Плакаты с элементами росписи, презентация в формате Microsoft Power Point ;
4. Раздаточный материал.
Ход занятия:
1. Повторение основных понятий по теме, закрепление навыка нахождения и построения оси симметрии фигуры
СЛАЙД 2
Как вы понимаете слова:
«Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство» Герман Вейль
Посмотрите на затейливый морозный узор на окне – чем не пример природной симметрии?

СЛАЙД 3
Что объединяет рисунки – изображения кленового листа, снежинки, бабочки?
Какая фигура называется симметричной?
Как проверить, являются ли фигуры симметричными?
Практическое задание 1. (Раздаточный материал – прямоугольники, квадраты, различные треугольники из бумаги) Путем перегибания выяснить, имеет ли фигура ось симметрии, количество осей симметрии.

СЛАЙД 4

Сколько осей симметрии имеет каждая из фигур? Показать.
Практическое задание 2. (Приложение 1). Раздаточный материал – карточка №1)
рис.1 Восстановить фигуру по сохранившимся частям и осям симметрии.
рис.2 Провести все оси симметрии фигуры
2. На Руси люди издревле старались украсить терема, церкви, предметы обихода. Они придумывали удивительные замысловатые орнаменты, узоры, в основе которых лежат различные виды симметрии. Сегодня мы рассмотрим виды традиционной росписи, вышивки, резьбы нашего родного края – районов Архангельской области.

СЛАЙД 5
Удивительно красива и своеобразна природа Севера. Алый цвет зари, зеленая трава, желтые лютики, голубые васильки, белоснежная россыпь таволги и светлое-светлое небо… Вот откуда яркие узоры в росписи художников нашего края.
СЛАЙД 6
Они повторяли то, что видели в родных просторах, лесах, озерах и реках. Вместе с росписью в жилище крестьянина входило лето и солнце даже в тёмный зимний день. Народные умельцы создавали неповторимую сказку, радующую глаз и согревающую сердце.
Со времен язычества, да и в христианстве, люди верили, что вещи, предметы быта, одежда, украшенные символическими узорами, оберегают жилище и человека от злых духов. Болезней, несут радость, здоровье и счастье.
Вниманию обучающихся предлагаются старинные полотенца, скатерти с вышивкой, салфетки, лоскутные покрывала, прялки, кринки, разделочные доски. Рассматриваются элементы орнаментов, симметрия. Особо обращается внимание на своеобразие вышивки тамбурным швом белыми нитями по красному полотну, встречающейся только в нашем Шенкурском районе.

СЛАЙД 7
Крестьянская изба снаружи всегда украшалась резьбой, росписью, начиная от калитки и до крыльца: «кони», «подзоры», «полотенца», резные наличники.
На фотографиях из музея деревянного зодчества Малые Корелы учащиеся определяют симметрию орнаментов.
Круг, разделенный радиусами на равные секторы, круг с крестом внутри – различные типы солнечных знаков. Солнце показывалось в трех позициях — левый край кровли (восходящее), верхний конек (полуденное солнце в зените), правый край – вечернее заходящее солнце. Заклинательным (обереговым) орнаментом украшали все проемы, чтобы всевозможные злые духи не могли проникнуть в жилище.

СЛАЙД 8
Для покрытия куполов церквей и часовен брали осину, из которой изготовляли так называемый «лемех» (тонкие дощечки с резными концами разной формы и величины). Такие купола серебрятся в лучах неяркого северного солнца.

СЛАЙД 9, 10,11
Вы видите костюмы Лешуконского народного хора. Это настоящие старинные традиционные вещи из сундуков бабушек и прабабушек. Найдите на одежде орнаменты, проследите симметрию узоров.
Практическое задание 3. ( Приложение 2 Раздаточный материал – карточка №2, №3)
Мальчики вырезают по заготовкам, используя вертикальную и горизонтальную осевую симметрию, резные украшения северных изб. Готовые резные узоры крепятся к доске, на схематичное изображение избы.
Девочки занимаются «вышивкой» — достраивают орнаментальные мотивы (темы плодородия, дождя, засеянных полей, неба и земли, подземного царства). Аналогичные рисунки выполняются и на доске.
Учитель комментирует символическое значение изображений в древнерусском орнаменте.



СЛАЙД 12
Бурак, бурачок, туес – это цилиндрический сосуд из бересты. С ним ходили по грибы да ягоды, наливали квас, ключевую воду, которая весь день оставалась холодной. Они расписывались ленточками-бордюрами, округлыми листочками и ягодками, цветами и птицами. Перед вами образцы пермогорской росписи, характерной для народных мастеров, проживающих на берегах Северной Двины, например Двинского Березника.

СЛАЙД 13,14
С 6-8 лет девочка в крестьянской семье начинала готовить себе приданое к свадьбе: пряла нитки на прялке, чтобы потом наткать полотна для полотенец, рубах и сарафанов. Отец делал маленькую прялочку дочери, а жених дарил своей невесте красивую расписную прялку, и шла она по деревне на посиделки, гордо неся ее, чтобы все видели эту красоту. Шенкурская роспись была распространена по всему течению реки Вага. По своей композиции, орнаменту, цветовой гамме она значительно отличается от других северных росписей. В основе рисунка три крупных цветка, нанесенных по центральной оси лопасти один над другим. В композиции главное – симметрия, равновесие. Орнаменты в виде лент (бордюры) широко применялись при оформлении предметов обихода.
Практическое задание 4. Изготовление бордюра: 1) Полоску бумаги сложить «гармошкой» и нарисовать какой-либо рисунок, касающийся линии сгиба. Вырезать фигуру, оставляя участки на линиях сгиба неразрезанными. Развернуть полученную «гармошку».
2) Предварительно ленту сложите вдвое вдоль, а затем «гармошкой». Вырежьте свою оригинальную ленту.

СЛАЙД 15
Мезенская роспись похожа на рисунки первобытных людей. Прялки расписывались мужчинами, для которых самым важным в хозяйстве являлись кони и олени.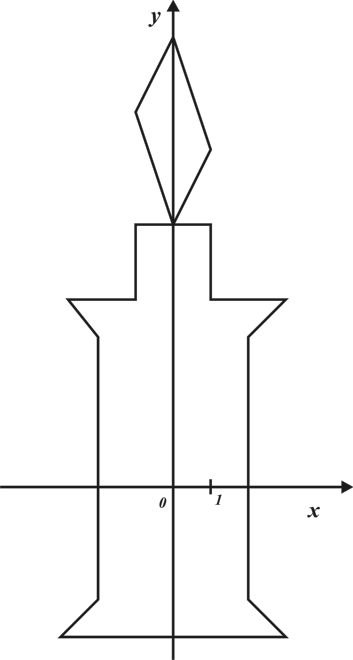 Характерной особенностью мезенской росписи является многоярусность. На нижнем и среднем рядах изображались олени, кони, а на верхнем – птицы. Это символизирует наземный, подземный и небесный мир. Решетка – принадлежность ткацкого станка, спиральки, черточки, кружочки – точно снежный вихрь от быстрой езды.
Практическое задание 5. ( Приложение 3 Раздаточный материал – карточка №4)
Восстановить элементы мезенской росписи по сохранившимся частям и осям симметрии.
(Представлены выполненные обучающимися работы)



СЛАЙД 16
Основным мотивом пучужской (верхнетоемской, северодвинской) росписи является древо жизни с симметрично расположенными на нем или около него птицами. Существует легенда, что среди бескрайних водных просторов, которые были началом всех начал, стояло дерево. От двух птиц, свивших на нем гнездо, началась жизнь на земле. Древо – символ жизни, а охраняющие его две птицы – символ добра и семейного счастья.
Практическое задание 6.
Показать на иллюстрациях пучужской росписи элементы осевой симметрии.

СЛАЙД 17
Лоскутное шитье – традиционное домашнее ремесло Важского края. Подбор лоскутов может быть совершенно произвольным в зависимости от вкуса, настроения мастерицы, от имеющегося материала, но в любом случае, их расположение соответствует какому-либо виду симметрии.
Практическое задание 7. (Приложение 4)
Можно ли указать ось симметрии на данном элементе лоскутного шитья? Используйте различные подходы: по виду ткани, по геометрическим фигурам.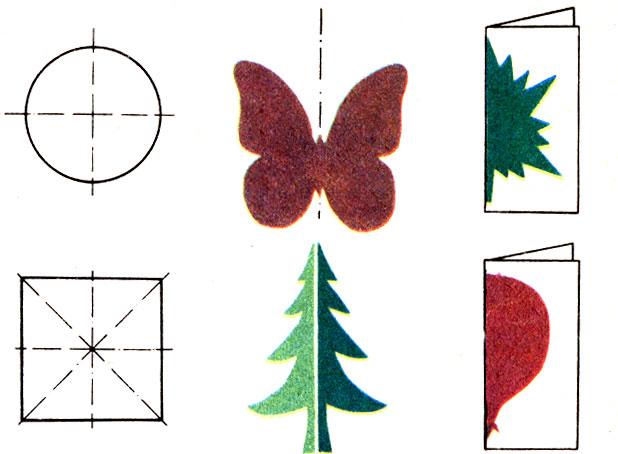

3. Заключение.
Ромбы, круги, квадраты – все это символы земли, солнца, неба, т.е. окружающего мира. А значит и вещь, сделанная вручную из лоскутков – это своеобразный оберег, который охраняет наш дом. Как из лоскутков ткани складывается целое покрывало, так из лоскутков времени складывается история целого края. Лоскутки эти могут быть темными и светлыми, маленькими и большими, но только наше отношение к жизни определяет: каким будет следующий лоскуток – радостно ярким или уныло тоскливым.
Вслушайтесь в стихотворные строки нашей Шенкурской поэтессы Надежды Князевой. О чем они?
Только бережное отношение к истории, самобытным традициям родного края позволяет проникнуться искренней любовью к малой родине и своей стране.
4. Домашнее задание:
Ребята, к этому занятию вы вырезали из бумаги снежинки. Все они имеют 4 или 8 осей симметрии. В природе снежинки имеют 6 осей симметрии. Найдите такой способ сгибания листа бумаги, чтобы полученная снежинка имела 6 осей симметрии.
Приложение 5: фотографии с описываемого занятия

Литература
1. Вергазова О.Б. Симметрия древнерусского орнамента.- Математика в школе, научно-теоретический и методический журнал- ООО «Школьная пресса», №6 2007.
2. Изместьева Л.А. Мезенская роспись. — Архангельск, АО ИППК, 1992.
3. Козлова Н.С. Пучужская роспись. – Архангельск, АО ИППК, 1993.
4. Пузенкова Л.А. Шенкурская роспись. — Архангельск, АО ИППК, 1995.
5. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия 5-6 классы – 3-е изд. — М.: Дрофа, 2000. 

Не удается найти страницу | Autodesk Knowledge Network

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}}*

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}  

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}} {{$select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}  

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$select.selected.display}} {{l10n_strings. CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Презентация «Симметрия вокруг нас»

Слайды и текст этой онлайн презентации

Слайд 1

Симметрия вокруг нас
Выполнил: ученик 11 «А» класса МБОУСОШ №54 г. Липецка Боровских Дмитрий Андреевич Руководитель: учитель по математике Цветкова Светлана Васильевна


Слайд 2

Содержание:
Определение симметрии Виды симметрии: центральная симметрия (симметрия относительно точки) осевая симметрия (симметрия относительно прямой) зеркальная симметрия (симметрия относительно плоскости) симметрия вращения Симметрия вокруг нас: симметрия человеческого тела в природе в архитектуре в быту в физике в химии в литературе Заключение


Слайд 3

Выдающийся математик Герман Вейль высоко оценил роль симметрии в современной науке.
«Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство». «Симметрия, обнаруживаемая и в жизни, и в искусстве, и в архитектуре, и в природе является одним из принципов гармоничного построения мира».
Толстой Л.Н. «Отрочество»
«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе.
Определение симметрии


Слайд 4

В геометрии: Симметрия (означает «соразмерность» ) — свойство геометрической фигуры, расположенной в пространстве или на плоскости, заключающееся в закономерном повторении равных ее частей.
Определение симметрии
В биологии: Симметрия в биологии — это закономерное расположение подобных (одинаковых) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии.


Слайд 5

Виды симметрии. Центральная симметрия (симметрия относительно точки)
Геометрическая фигура ( или тело ) называется симметричной относительно центра , если для каждой точки B этой фигуры может быть найдена точка B’ этой же фигуры, так что отрезок BB’ проходит через центр C и делится в этой точке пополам ( BO = OB’ ). Точка O называется центром симметрии и считается семетричной самой себе.


Слайд 6

Центральную симметрию имеют многие геометрические тела. К ним следует отнести все правильные многогранники (за исключением тетраэдра), все правильные призмы с четным числом боковых граней, некоторые тела вращения (эллипсоид, цилиндр, гиперболоид, тор, шар). Центр симметрии многогранников указывает на наличие двух равных и взаимно параллельных граней. Например, у параллелепипеда (рис.5.6) грань АА1’В1’В равна и параллельна грани В1В1А1А1. Рассмотрим симметричность вершин. Точке А симметричны две точки А1. Одна — относительно центра симметрии многогранника, другая — относительно центра симметрии грани. В свою очередь, точкам А1 симетрична точка А1′ и т.д. Как видно из чертежа, грани параллелепипеда и прямо, и обратно параллельны. В случае октаэдра (рис.5.7) имеется только обратная параллельность граней, например, АВС и А1В1С1.


Слайд 7

Осевая симметрия (симметрия относительно прямой)
Примером может служить лист тетради, который согнут пополам, если по линии сгиба провести прямую линию (ось симметрии). Каждая точка одной половины листа будет иметь симметричную точку на второй половине листа, если они расположены на одинаковом расстоянии от линии сгиба на перпендикуляре к оси.
Две точки A и A1 называются симметричными друг другу относительно прямой a, если эта прямая перпендикулярна отрезку AA1 и проходит через его середину. Прямую a называют осью симметрии. Каждая точка прямой a считается симметричной самой себе.


Слайд 8

Прямоугольник ABCD имеет две оси симметрии: прямые m и l. Если чертеж перегнуть по прямой m или по прямой l, то обе части чертежа совпадут.
Квадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s. Если квадрат перегнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
Окружность с центром в точке О и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые: m, m1, m2, m3 …


Слайд 9

Зеркальная симметрия (симметрия относительно плоскости)
Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой фигуры может быть найдена точка E’ этой же фигуры, так что отрезок EE’ перпендикулярен плоскости S и делится этой плоскостью пополам ( EA = AE’ ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова (например, левая перчатка не подходит для правой руки и наоборот ). Они называются зеркально равными.


Слайд 10

Предметы могут иметь одну, две, три и т.д. плоскостей симметрии. Например, прямая пирамида (рис.5.2а и 5.За), основанием которой является равнобедренный треугольник, симметрична относительно одной плоскости Р. Призма с таким же основанием (рис.5.2б и 5.3б) имеет две плоскости симметрии. У правильной шестиугольной призмы (рис.5.2в и 5.Зв) их семь. На рисунке не изображены те из них, которые подобно плоскостям Р и О, проходят через остальные диагонали и апофемы оснований. Тела вращения: шар, тор, цилиндр, конус и т.д. имеют бесконечное количество плоскостей симметрии.


Слайд 11

Тело ( фигура ) обладает симметрией вращения, если при повороте на угол 360°/n ( здесь n – целое число ) вокруг некоторой прямой AB ( оси симметрии ) оно полностью совпадает со своим начальным положением. При n = 2 мы имеем осевую симметрию..
Симметрия вращения


Слайд 12

Симметрия вокруг нас. Симметрия человеческого тела
Билатера́льная симме́трия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Этот тип симметрии характерен для большинства животных, включая человека. У билатерально-симметричного существа отличаются верхняя и нижняя, передняя и задняя части, и только правая и левая идентичны и являются зеркальным отображением друг друга.
Витрувианский человек Леонардо да Винчи, изображающий симметрию человека. Рисунок часто используется как неявный символ внутренней симметрии человеческого тела, и далее, Вселенной в целом.


Слайд 13

В природе
На явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. Установлено, что в природе наиболее распространены два вида симметрии — «зеркальная» и «лучевая» («радиальная”) (форма симметрии, при которой тело совпадает само с собой при вращении объекта вокруг определённой точки или прямой) симметрии.
«Зеркальной» симметрией обладает бабочка, листок или жук и часто такой вид симметрии называется «симметрией листка» или «билатеральной симметрией».
К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется «ромашко-грибной» симметрией.


Слайд 14

Еще в 19-м веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел: »Все то, что растет или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой («ромашко-грибной») симметрии. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии — «симметрии листка» (одна плоскость симметрии)».


Слайд 15

Слайд 16

Слайд 17

Лёд — это уникальное вещество, способное образовывать более десяти различных кристаллических структур. снежинок.
Разгадка загадочной симметрии снежинок кроется в кристаллической решетке льда.
Практически весь лёд на планете кристаллизуется в гексагональной сингонии — его молекулы образуют правильные призмы с шестиугольным основанием. Именно шестиугольная форма решётки в конечном счёте обусловливает шестилучевую симметрию


Слайд 18

В архитектуре
Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство зданий зеркально симметричны. Общие планы построек, фасады, орнаменты, карнизы, колонны обнаруживают соразмерность, гармонию.
Композиция здания очень важна. От нее в первую очередь зависит впечатление, которое производит архитектурное сооружение. Сочетание различных объемов — высоких и низких, прямолинейных и криволинейных, чередование пространств — открытых и закрытых — вот основные приемы, которыми пользуется зодчий, создавая архитектурные композиции.
Наиболее ясны и уравновешенны здания с симметричной композицией. Такие здания были характерны для архитектуры эпохи классицизма.


Слайд 19

Слайд 20

Слайд 21

Но природа не терпит точных симметрий! Природа почти симметрична, но не абсолютно симметрична! Так, планетные орбиты, которые ещё Пифагором мыслились в виде совершенных окружностей, на самом деле оказались почти окружностями, но всё-таки не окружностями, а эллипсами. Нарушение симметрии обнаружено во многих явлениях ядерной физики. Помимо симметрии существует также понятие ассиметрии: Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. Примером удивительного сочетания симметрии и асимметрии является Покровский собор (храм Василия Блаженного) на Красной площади в Москве.


Слайд 22

Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!


Слайд 23

В быту
Орнамент — узор, основанный на повторе и чередовании составляющих его элементов. Предназначается для украшения различных предметов, архитектурных сооружений, произведений пластических искусств.


Слайд 24

Бордюр — это узкая полоса обоев, предназначенная для декоративного оформления помещения.


Слайд 25

В теоретической физике, поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения).
В физике
Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.


Слайд 26

В химии
Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается на специфике физических и химических свойств молекул в изолированном состоянии, во внешнем поле и при взаимодействии с другими атомами и молекулами. Большинство простых молекул обладает элементами пространственной симметрии равновесной конфигурации: осями симметрии, плоскостями симметрии


Слайд 27

В литературе
Палиндромами называют слова, предложения, стихи или иные произведения, которые читаются одинаково как с начала, так и с конца (имеют симметричный порядок букв)
ПРИМЕРЫ: А муза рада музе без ума да разума. A роза упала на лапу Азора. Вот сила типа капиталистов. Ешь немытого ты меньше! Кит на море романтик. Коту скоро сорок суток. Леша на полке клопа нашел. Мак чужд жучкам. Меня истина манит сияньем. Морда казака за кадром. Oколо Миши молоко. Он в аду давно. Ранил укусом осу кулинар. Тени нет. Я с леди все же свиделся.


Слайд 28

Заключение

Симметрия — это не только математическое понятие. Его заимствовали из природы. А так как человек — это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Когда мы видим проявление симметрии в живой и неживой природе, то невольно испытываем чувство удовлетворения тем всеобщим, как нам кажется, порядком, который царит в природе. И даже при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.


Слайд 29

Симметрия цветов: нарисуйте отсутствующие подсказки половин искусства

Используйте симметрию цветов как способ объяснить детям симметрию, а затем создавайте красивые симметричные цветочные рисунки с помощью этих печатных подсказок «Нарисуй недостающую половину»!

Объяснение концепции симметрии не должно быть абстрактным и теоретическим. Хорошим началом разговора о симметрии с детьми может стать взгляд в зеркало. Как оказалось, подавляющее большинство животных, включая человека, примерно симметричны.Как и растения. Фактически, симметрия и природа составляют выигрышную комбинацию — красивое, красочное и практическое занятие!

Раньше мы предлагали печатные художественные подсказки для изучения симметрии с насекомыми (рисунки) и с листьями (настоящие). Нашим детям нравятся подсказки, в которых им предлагается создать недостающую половину объекта, исходя из понимания того, что она симметрична половине на картинке. Это сложно, но весело! Мой сын с трех лет выдает подсказки каждый год.До сих пор его любимая стая состояла из недостающих половинок насекомых. Но этой весной мы решили взглянуть на цветы. Моему сыну тоже понравилась эта цветочная упаковка. Ему не терпелось поработать над этим!

Цветы очень интересны — с их помощью можно изучать не один, а два типа симметрии.

Симметрия цветов

Во-первых, двусторонняя симметрия. Что-то можно назвать билатерально-симметричным, если можно увидеть примерно зеркальное отражение половин по обе стороны от разделяющей плоскости — одинаковые левая и правая стороны.Люди двусторонне симметричны, как и 99% других животных, включая насекомых, как видно из подсказок к рисованию насекомых. Цветы тоже можно рассматривать как двусторонне-симметричные, хотя бы под определенным углом.

Но на самом деле многие цветы радиально симметричны. Этот тип симметрии встречается реже. Некоторые примеры включают медузы, морские звезды, многие вирусы и цветы. Радиальная симметрия описывает объекты, которые напоминают пирог, где несколько плоскостей разреза дают примерно одинаковые части, расходящиеся от центральной точки.Другими словами, если объект радиально симметричен, вы можете представить, как он выглядит, даже если вы видите только четверть его (или, в зависимости от объекта, одну десятую или даже меньше).

Набор для печати цветочной симметрии для детей

Пакет «Симметрия цветов» состоит из десяти цветов — тюльпана, подсолнечника, гвоздики, ириса, ромашки, нарцисса, лилии каллы, гардении, незабудки и орхидеи. Есть десять подсказок для рисования, исследующих концепцию двусторонней симметрии, и пять подсказок для рисования, исследующих концепцию радиальной симметрии.

Базовое понимание симметрии необходимо для заполнения художественных подсказок, поскольку они показывают только половину цветка (в случае двусторонней симметрии) и примерно четверть цветка (в случае радиальной симметрии). Детям предлагается самостоятельно нарисовать остальное, основываясь на том, что они видят, и на своем понимании симметрии!

В процессе дети должны обращать внимание на соответствие цветов, рисование правильных форм и подсчет правильного количества лепестков, листьев.В целом, эта деятельность имеет большое значение для отработки различных элементарных математических навыков.

И это действительно весело! Это может быть как простое, так и сложное занятие, которое очень хорошо адаптируется к разному возрасту, так что дошкольник может участвовать вместе со взрослым. Признаюсь, мне нравится рисовать пару картинок вместе со своими детьми, когда они над ними работают.

Как использовать набор для печати «Симметрия цветов»

Во-первых, поговорите с детьми о симметрии. Есть два плаката. Помогло бы иметь под рукой настоящий цветок или лист.

После этого просто распечатайте и рисуйте! Можно использовать карандаши, фломастеры, ручки — все, что угодно. Если вы хотите использовать краски, печатайте на более плотном картоне. Если вы хотите снова и снова использовать его с разными учениками, ламинируйте и используйте маркеры сухого стирания.

Также попробуйте!

Нарисуйте недостающую половину: насекомые

Нарисуйте недостающую половину: Транспортные средства

Когда вы воспользуетесь подсказками, мы будем рады увидеть ваше искусство симметрии! Отметьте нас в facebook или instagram (@ adventureinabox ).

советов по рисованию симметрии | Sciencing

На симметричном чертеже есть идентичные части, отражающие друг друга по линии симметрии. Эту симметрию можно найти во всей природе, включая человеческое тело, форму листьев и крыльев бабочки. Создание искусства, демонстрирующего симметрию, может быть трудным, поскольку две половинки, пересекающие линию симметрии, должны быть идентичны. Художник использует практику и несколько полезных руководств, чтобы рисовать симметричные изображения.

Практика зеркального отображения

Вы можете практиковать симметрию в рисовании, практикуясь с зеркалом.Проведите прямую линию с помощью линейки на вертикальной или горизонтальной оси. С одной стороны от прямой нарисуйте половину фигуры. Например, нарисуйте половину креста или сердечка. Используйте линейку, чтобы определить размеры нарисованной вами половинки. Используйте эти измерения, чтобы создать зеркальное отображение полуформы на другой стороне линии симметрии. Практикуйтесь в использовании различных форм, например, с прямыми линиями и углами, а также с изогнутыми линиями. Чем больше у вас будет практики с основными формами, тем лучше вы будете позже создавать более детализированные симметричные изображения.

Линии сетки

Сетки — еще один способ создания симметричных изображений. Нарисуйте сетку, используя отметки светлым карандашом и линейку. Важно, чтобы все линии сетки были прямыми, а прямоугольники были одинакового размера. Если коробки неправильные, рисунок тоже будет. Определите, какая линия сетки является центром или линией симметрии сетки. Нарисуйте половину изображения, которое вы хотели сделать. Используйте сетки как способ измерения расстояния от линии симметрии и размера объектов.Как только рисунок будет завершен, сотрите все линии сетки.

Произвольный набросок

Произвольный набросок также можно использовать для тренировки симметрии. Используйте изображение объекта в качестве ориентира и от руки нарисуйте основной контур объекта. Используйте легкие карандашные отметки, чтобы создать набросок от руки, потому что большая часть этих отметок будет стерта или изменена позже. Определите, где находится линия симметрии на объекте, и с помощью линейки проведите эту линию. Используйте набросок в качестве ориентира, чтобы добавить более подробные изображения на одну сторону линии симметрии.Создайте зеркальное отображение детального изображения на другой стороне линии симметрии.

Лица

Лица сложно нарисовать, и они редко бывают идеально симметричными. Однако вы можете попрактиковаться в рисовании симметричных лиц с помощью фотографий. Возьмите изображение лица и проведите вертикальную линию через центр носа, чтобы создать линию симметрии. Вырежьте изображение по этой линии. Прикрепите к изображению белый лист бумаги, чтобы нарисовать другую сторону лица. Вначале может быть полезно использовать технику сетки, чтобы запечатлеть все черты лица.По мере улучшения удалите сетку и нарисуйте зеркальное отображение лица.

Изучение художественных концепций — рабочие листы с линиями симметрии

Изучите концепцию симметрии с этими рабочими листами с линиями симметрии. Простые подсказки для рисования «половин» помогут вам, художники!

Что такое симметрия…

Симметрия — это качество изготовления одинаковых частей, обращенных друг к другу или вокруг оси. Симметрию можно увидеть везде — в природе, графическом дизайне, архитектуре, даже в людях.Как только ваши дети поймут, что такое симметрия, они смогут распознать ее, глядя на чужие работы, и использовать ее как инструмент в своих собственных работах.

Создавая симметричные изображения, которые составляют только половину, ваш молодой художник вдохновляется рисовать оставшуюся часть изображения.

Для большей симметрии художественных идей прочтите этот пост. Более элементарный рабочий лист симметрии плюс классический проект симметрии с полным видеоуроком завершат ваше исследование симметрии.

Различные виды симметрии….

Отражательная симметрия — линия может быть проведена посередине фигуры, а фигура на одной стороне линии «отражается» на другую сторону. Отраженная форма будет точно такой же, как оригинал.

Радиальная симметрия — состояние, при котором аналогичные части равномерно расположены вокруг центральной оси.

Существуют и другие, более специфические виды симметрии, такие как симметрия вращения , двусторонняя и диагональная симметрия . На мой взгляд, понимание основных концепций отражающей радиальной симметрии упрощает понимание других концепций.Эти термины могут быть добавлены в словарный запас ваших студентов по мере необходимости.

Вы хотите сегодня взять эти рабочие листы симметрии….

Вы можете использовать их дома или в классе — бесплатно! Используйте форму ниже, чтобы стать подписчиком KTC. Затем проверьте свою электронную почту и подтвердите подписку. После подтверждения вы получите еще одно электронное письмо с паролем только для подписчика. Этот пароль откроет мою бесплатную библиотеку ресурсов, где вы найдете эскиз этих таблиц симметрии под заголовком «Элементы, принципы и связанные концепции.”Щелкните миниатюру, и PDF-файл выскочит прямо.

Вы также получите доступ к сотням других бесплатных печатных форм, которые помогут вам проявлять творческий подход с вашими детьми. Кроме того, я работаю над тем, чтобы поделиться растущим числом цифровых ресурсов, таких как действия в Google Slides, которыми вы можете поделиться со своими детьми!

Подписавшись, вы также начнете получать мои электронные письма KTC. Мои новейшие веселые проекты и бесплатные ресурсы для печати будут доставлены прямо в ваш почтовый ящик!

Вы уже являетесь подписчиком Kitchen Table Classroom….

Если да, то вам не нужно подписываться снова, просто чтобы получить эти забавные листы симметрии. Просто используйте этот пароль подписчика для входа в систему и загрузки.

Если вы потеряли пароль, потому что вы человек, и это то, что мы делаем, не волнуйтесь! Проверьте нижнюю часть любого информационного бюллетеня от меня. Вы увидите ссылку на мою библиотеку ресурсов и пароль.

Знаете ли вы кого-нибудь еще, кому нужны эти рабочие листы с линиями симметрии? Поделись, пожалуйста!

Каждая публикация в социальных сетях помогает мне предлагать вам больше увлекательных проектов и бесплатных печатных листов искусства, подобных этим!

Кажется, мы не можем найти эту страницу

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

5.10. Диалог «Рисование симметрии»

5.10. Диалог рисования симметрии

5.10. Диалог рисования симметрии

Рисование симметрии — это новая функция рисования в GIMP-2.10 при поддержке инструменты на основе кисти (Карандаш, Кисть, Ластик, Аэрограф, Кисть MyPaint, Clone, Smudge, Dodge), а также инструмент Ink. Есть несколько видов симметрия, все настраивается.

5.10.1. Активация диалога

Вы можете получить доступ к этому диалоговому окну из строки меню изображения через: → →

Диалог «Рисование симметрии» стыкуется.Прочтите Раздел 2.3, «Диалоги и стыковка», чтобы узнать больше. о концепции стыковки.

5.10.2. Использование диалогового окна «Рисование симметрии»

Рисунок 15.85. Диалог рисования симметрии

Этот диалог очень прост. У вас есть только симметрия элемент с раскрывающимся списком, который предлагает четыре варианта.Как только вы проверите тип симметрии, оси симметрии отображаются на изображении как пунктирные зеленые линии окно, и вы можете начать рисовать выбранной кистью.

Опции

никто

Это вариант по умолчанию; рисование симметрии не активировано.

Зеркало

Рисунок 15.86. Диалоговое окно «Зеркальное отражение симметрии» .

Это симметрия, как в зеркале. Вы можете выбрать Горизонтальная симметрия, Вертикальная симметрия или центральная симметрия. Ты также можно выбрать несколько симметрий.

Положение оси симметрии по умолчанию — середина изображения. окно. Вы можете разместить ось там, где хотите, используя Положение горизонтальной оси и Положение вертикальной оси.

Отключить преобразование кисти: при преобразовании рисунок, сама кисть тоже преобразится. Для Например, при зеркальном преобразовании не только ваш рисунок на правая часть холста должна быть зеркально отражена слева, но сама кисть очевидно «перевернутый» слева. Если по какой-то причине вы хотите нарисованные линии должны быть отражены (или другое преобразование), но не сам контур кисти, вы можете установить этот флажок.По понятной причине вы не увидите этого с симметричными кистями. хоть. Вот почему вы не видите эффекта, так как многие по умолчанию кисти симметричные.

Черепица

«Тайлинг» — это трансляционная симметрия, которая может быть конечный (с максимумом штрихов) или бесконечный. В последнем случае, это идеальный инструмент для создания узоров или бесшовных плиток на время покраски.

Рисунок 15.87. Диалог мозаики симметрии

В этом режиме изображение покрывается штрихами.

Здесь нет топоров. Возможные варианты:

• Интервал X Интервал Y: это интервалы по осям X и Y в пикселях между инсультные центры.

• Shift: это сдвиг между линиями на Ось X в пикселях.

• Макс ходов X, Макс. штрихов Y: это максимальное количество кистей штрихи по осям X и Y. По умолчанию 0, что означает отсутствие ограничений, по размеру изображения.

Мандала

Рисунок 15.88. Диалог «Симметрия мандалы»

Штрихи нанесены вокруг центра координат оси.

Возможные варианты:

• Центр абсцисс, Центр ордината для позиционирования центра координат.

• Количество баллов: количество штрихов.

• Отключить преобразование кисти: см. Выше.

Кисточка для перца выбрана. Используется карандаш.

Пример для зеркала

Рисунок 15.89. Вертикальная симметрия




Пример плитки




Пример для мандалы




Как рисовать симметричные глаза

Чтобы начать рисовать симметричные глаза, нам нужно будет провести несколько линий, чтобы определить форму первого глаза.Как мы узнали в нашем уроке, как рисовать пропорции лица, мы можем использовать глаз как инструмент измерения при разделении других частей лица.

Мы видели, как мы можем измерить длину одного глаза для промежутка между глазами, а затем использовать ту же длину, чтобы затем определить местоположение второго глаза. В результате мы получим три равные части с идеальными пропорциями.

Если вы чувствуете необходимость использовать линейку, потому что вы только начинаете рисовать лицо, это нормально, но по мере того, как ваши навыки продолжают развиваться, попробуйте поработать над оценкой этих расстояний без линейки.Это сэкономит вам много времени в будущем.

Используя горизонтальные измерительные линии, вы выберете важные ориентиры, такие как внутренний и внешний угол глаза, и проведете линии, проходящие через них. Обозначьте эти места на другой стороне и используйте их, чтобы нарисовать глаза. Вам просто нужно «соединить точки».

Если вы рисуете в цифровом формате, вы можете почувствовать желание просто скопировать один глаз и перевернуть его. Это быстрый и простой способ получить точную копию глаза, но вы, вероятно, захотите немного отрегулировать второй глаз, чтобы получить некоторые небольшие различия.

Однако лучше, чем копирование, состоит в том, что вы работаете над своей слабостью и просто продолжаете практиковаться в сопоставлении разных глаз, потому что это улучшит ваши навыки не только в рисовании глаз, но и в сопоставлении любого вида симметричного объекта или частей лица.

Добавьте детали, такие как ресницы, радужную оболочку и зрачки, и все остальное, например брови. Когда вы закончите, вы можете стереть вспомогательные линии, которые вы создали, чтобы они соответствовали размерам.

На самом деле хорошо иметь небольшие отклонения, которые делают каждый глаз уникальным.Вы обнаружите, что люди ценят аутентичность выше идеальной симметрии.

Эту технику можно использовать каждый раз, когда вы хотите дважды проверить свою симметрию; будь то лицо, ваза или машина — значения не имеет. Но, как было сказано ранее, это должен быть скорее инструмент для обучения, и чем больше вы разовьете свой художественный глаз, тем лучше вы будете замечать симметричные предметы.

НАЗНАЧЕНИЕ

Единственный способ попрактиковаться в этой технике рисования симметричных глаз — это использовать ее.Найдите любой тип глазных наборов, иногда забавно смешивать их и использовать забавные или развлекательные наборы глаз для практики. В любом случае, используйте эту технику, чтобы создать двадцать пар глаз, сделав их максимально симметричными вручную.

Рисование здания Капитолия США с использованием симметрии (C3W2)

На второй неделе нашего года классических бесед (CC) у нас всегда есть художественный проект, основанный на симметрии или «зеркальном отображении», как сказано в Руководстве по основам CC. Это веселая неделя, которая включает в себя небольшую нагрузку на мозг, но она важна как для того, чтобы стать более опытным художником, так и для поддержки многих исследований, не связанных с искусством.Поскольку мы изучаем американскую историю и географию во втором цикле, я подумал, что здание Капитолия США станет отличным художественным проектом. Мы также можем проскользнуть в короткое двадцатисекундное объяснение здания, чтобы помочь студентам связать точки между нашим художественным проектом и соответствующими исследованиями истории и географии!

Симметрия — отличная концепция, которую могут понять даже самые маленькие ученики. Мы видим это в искусстве, но также и в социальных взаимодействиях, биологии, химии, физике и математике. Фактически, концепции симметрии встречаются на многих уровнях математики, от геометрии и вероятности до алгебры, исчисления и других.Это также отличный пример «инвариантности» (когда что-то не меняется в результате набора преобразований). По мере того, как учащиеся учатся в школе, концепция симметрии будет использоваться снова и снова.

Изучение симметрии в искусстве проясняет идею симметрии для учащихся и дает им более глубокое понимание симметрии. Изучение симметрии также помогает нам стать лучшими художниками, потому что мы часто намереваемся рисовать объект симметрично, но в итоге получается однобокий. Потратив время на то, чтобы попрактиковаться в рисовании симметричных предметов, художники научатся рисовать сбалансированные (не однобокие) объекты.Упражнения по рисованию симметрии также помогают нам всем стать лучшими художниками, поскольку мы ищем то, что есть на самом деле, а не то, что, по нашему мнению, должно быть.

Этот проект будет очень похож на проект по рисованию симметрии, который мы выполняли в прошлом году. Мы начнем с небольшого разогревающего упражнения, которое поможет ученикам научиться рисовать вторую половину симметричного объекта. В прошлом году у меня было шесть изображений на листе для разминки, и я подумал, что это заняло слишком много времени. Итак, в этом году на разминке всего 3 изображения.Все они являются американскими достопримечательностями, чтобы соответствовать нашей теме.




Затем мы воспользуемся упрощенным линейным рисунком здания Капитолия США, сложенным пополам, чтобы нарисовать сначала одну половину, а затем вторую половину здания Капитолия. Я создал полный план урока для этого арт-проекта, который включает:

• Сценарий, объясняющий:
  • симметрия
  • как симметрия используется во многих предметах
  • как симметрия используется для создания баланса в искусстве (на примере Тайная вечеря )
  • где и что такое U.S. Capitol Building есть и когда было построено
• Цветная копия картины Леонардо да Винчи Тайная вечеря
• Разминка с тремя американскими достопримечательностями (мост Золотые Ворота, Арка Ворот и здание Капитолия США)
• Подробная инструкция арт-проекта
• Варианты увеличения или уменьшения масштаба художественного проекта в зависимости от уровня опыта ваших студентов-художников
• Штриховой рисунок здания Капитолия США (западная сторона)
• Упрощенный штриховой рисунок U.