Рисунок кубика: Академический Рисунок Куба Карандашом (Как Нарисовать?)
23.06.2023 
Разное
Четырёхмерный кубик
Валерия Сирота
«Квантик» №7, 2022
Когда я была маленькой, мама и папа научили меня рисовать кубик. Наверное, вы все знаете: нужно сначала нарисовать квадрат — это передняя сторона кубика, которая «смотрит на нас»; потом провести из каждой вершины (угла) квадрата отрезки одинаковой длины и в одном и том же направлении — это горизонтальные рёбра кубика, которые ориентированы «от нас». Дальше четыре конца этих отрезков соединяем, получается ещё один квадратик — это задняя грань кубика. Вот и всё! Получился вид «со стороны передней грани и чуть сверху-сбоку». Если кубик не проволочный, а «сплошной» (непрозрачный), нужно стереть или лучше сделать пунктирными рёбра, которые скрыты за тремя ближайшими гранями — на рисунке 1 это передняя, верхняя и правая.
Проще простого, да? Но мои родители были математики. Поэтому они на этом не остановились и научили меня рисовать ещё и четырёхмерный кубик.
Это тоже оказалось просто! Надо только разобраться, что такое это четырёхмерье.
Мы все живём в трёхмерном мире. Потому что у нас есть три независимых направления, вдоль которых мы можем перемещаться или хотя бы смотреть на разные вещи: вперёд-назад, вверх-вниз и вправо-влево. Вперёд-назад — считается за одно направление, потому что движения «туда» и «обратно» не независимы, а противоположны друг другу: одно может «отменить» действие другого, и, пройдя шаг вперёд, а потом шаг назад, вы вернётесь в ту же точку. А вот сделав шаг вправо, а потом несколько шагов вперёд, вы в ту же точку не вернётесь. Направление «по диагонали» тоже не независимое — это комбинация уже имеющихся. Ведь можно пройти по диагонали вверх-направо, а можно вместо этого пройти сначала вверх, а потом направо, и прийти в ту же точку (рис. 2).
Можно представить себе двумерных муравьишек, живущих в плоскости. Например, нарисованных на экране компьютера. (Для определённости давайте считать, что плоскость вертикальна.) У них только два независимых направления, вверх-вниз и влево-вправо, выйти из плоскости они не могут.
Cложная у них жизнь: если встретятся двое на дорожке, то, чтобы идти дальше каждому своей дорогой, придётся одному через другого перепрыгнуть. Или как им открывать двери в домах? Ещё сложнее жизнь у одномерных червяков, живущих на линии. Они вообще не разминутся при встрече, ползают только друг за другом… и если построят стенку (точку на линии), за неё никто не проникнет, никаких дверей нет.
Но сейчас речь не о них, а о других воображаемых (а может, и нет?) существах, живущих в мире с четырьмя измерениями. Кроме направлений вверх-вниз, вправо-влево и вперёд-назад у них есть ещё одна пара, ещё одно направление, которое мы и представить не можем, и даже названия для этого у нас нет. Так же как двумерные, плоские человечки не могут представить, что есть что-то «снаружи» их листа бумаги.
Но — удивительно! — хоть представить и нельзя, а нарисовать можно. Ведь трёхмерный куб тоже не помещается в двумерную плоскость, но мы ухитряемся нарисовать его на ней. Просто мы выбираем направление на плоскости, которое изображает третье измерение; те самые параллельные друг другу наклонные палочки на рисунке 1 — рёбра «от нас» — как раз ориентированы вдоль этого третьего направления.
На плоскости оно совсем не независимое, но мы «забываем» об этом, чтобы увидеть в нарисованном наборе палочек не плоскую фигурку, а объёмный кубик.
Чтобы показать на плоскости четвёртое измерение, нужно просто выбрать ещё одно направление, которое его изображает. Да и какая для плоскости разница — третье измерение или четвёртое? Они всё равно в неё оба не помещаются.
Итак, рисуем четырёхмерный кубик. По дороге вспоминаем, как мы рисовали трёхмерный (а ведь могли бы его нарисовать и двумерные человечки): передняя и задняя грани — в плоскости рисунка, только со сдвигом одна от другой. Горизонтальные рёбра боковых граней — все параллельны направлению «вдаль».
Трёхмерный куб составлен из квадратных граней («двумерных кубов»), которые склеиваются между собой по рёбрам. Четырёхмерный куб будет состоять из трёхмерных «3-граней», то есть обычных кубиков, которые будут склеиваться по двумерным граням.
Сначала рисуем (по старому рецепту) «обычный» трёхмерный куб — это «передняя» в том, четвёртом, измерении, трёхмерная грань 4-кубика.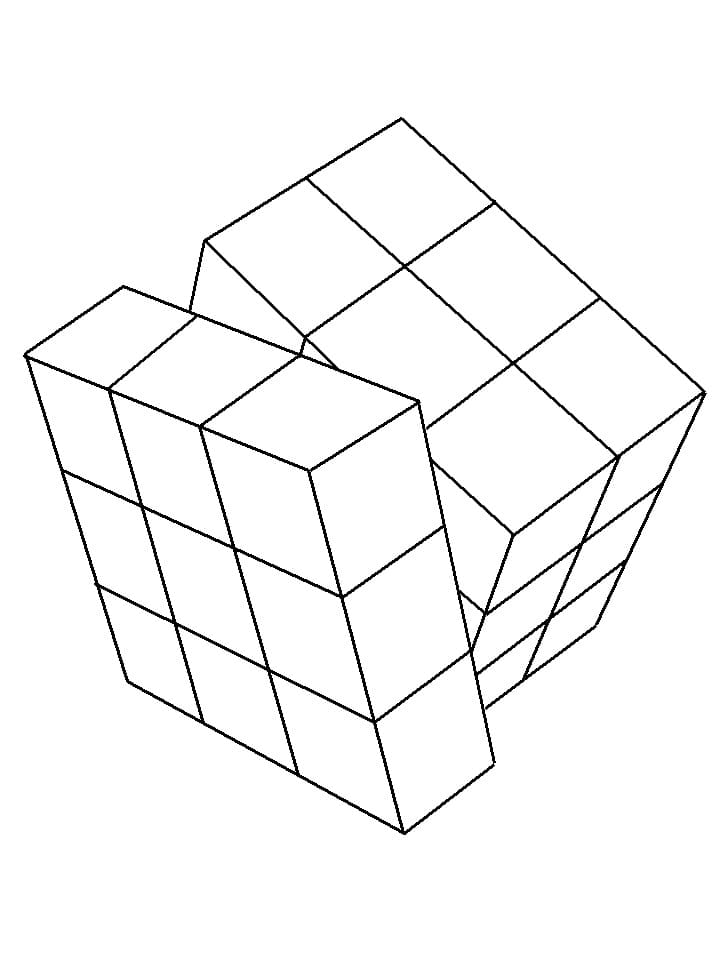
На рисунке 4 она показана чёрными рёбрами. Потом из каждой вершины этой «передней 3-грани» проводим палочку-ребро в направлении четвёртого измерения (на рисунке — красные): все боковые 3-грани параллельны направлению «в неизвестность». И, наконец, рисуем «заднюю 3-грань» — ещё один кубик, сдвинутый относительно первого (на рисунке — синий). Вот и всё!
Чтобы хвастаться перед одноклассниками, этого уже достаточно. Но чтобы лучше разобраться, что же это нарисовано, ответим ещё на несколько вопросов.
Эту задачу можно решить разными способами. Мы их сейчас обсудим, и решение найдём. Но прежде, чем читать дальше, попробуйте разобраться самостоятельно. Может быть, вы справитесь и сами!
Обратите внимание, что на рисунке 4 не все 3-грани выглядят как кубики, некоторые — как параллелепипеды, и вовсе не прямоугольные: для примера мы раскрасили одну 3-грань (рис. 5). Это не беда, и в обычном рисунке трёхмерного куба не все грани — квадраты. Но если вас это расстраивает, можно рисовать посимметричнее, чтобы все 3-грани выглядели почти кубами — как на рисунке 6.
Кто сколько тут видит кубиков?
Если вы не знаете, как подступиться к четырёхмерному кубику — вот пара задачек-подсказок, чтобы с ним познакомиться.
Решение задачи 0.
Первый способ — непосредственное усмотрение истины из нарисованной картинки. В ней ведь всё есть — и вершины, и рёбра, и все грани… Стоит лишь повнимательнее вглядеться. Но, действуя так, легко ошибиться — недосчитать что-нибудь или, наоборот, подсчитать дважды. Поэтому предлагаю другой способ.
Он основан на идее «подсчёт двумя способами», популярной в олимпиадной математике. Например: из трёх сестёр у каждой по 2 котёнка, а у каждого из котят — по 2 хозяйки; сколько всего котят? Можно представить себе, что каждая хозяйка надела на своего котёнка поводок, и сосчитать поводки. Вот и здесь можно считать двумя способами всё подряд — рёбра, грани…
Сначала всё-таки подсчитаем «в лоб» число вершин, вспомнив, как мы рисовали: у квадрата 4 вершины, у трёхмерного куба 8 (ещё 4 на дальней грани), для 4-мерного куба мы каждую из них продублировали.
Итого 8 + 8 = 16. Теперь заметим, что из каждой вершины 4-мерного куба торчит 4 ребра — достаточно проверить для ближайшего угла, они все одинаковы. Итого 16∙4 кончиков рёбер. Но у каждого ребра 2 конца, значит, nвершин ∙4=nрёбер 2; nрёбер=16∙4:2=32. Легче ведь так, чем подсчитывать по рисунку?
Теперь — опять глядя на ближайший угол картинки — можно сообразить, что к одному ребру «прикреплено» 3 грани. Две — из нашего старого кубика и ещё одна — уходящая «в неизвестность», в четвёртую сторону. А сколько рёбер у каждой грани, все знают; значит, умножая число рёбер на 3, мы каждую грань сосчитаем 4 раза. Дальше уж досчитайте сами! И не забудьте ещё разобраться с 3-гранями — трёхмерными кубиками, из которых складывается 4-мерный куб.
Если вам не понравился этот способ или всё с ним ясно, но хочется понять, как решать и другие задачи про «четырёхмерье», вот ещё способ — координатный.
На плоскости можно выбрать две оси — вправо и вдаль, например, если эта плоскость горизонтальная, — и записывать положение любой точки двумя числами: (x, y).
Вы так делали в школе. Или дома, играя в морской бой, только там одну цифру заменяют буквой. Эти два числа показывают, сколько надо пройти вдоль каждой оси, двигаясь из начала координат, чтобы прийти в нужную точку. Если добавить третью ось — вверх — и третье число z, можно этими тремя числами описывать положение точки во всём трёхмерном пространстве. А в четырёхмерном нужно ещё четвёртое число — назовём его u: оно показывает, на сколько надо сдвинуться в «ту», четвёртую сторону.
Теперь разберёмся с кубиками разных размерностей. Пусть длина стороны кубика равна 1, один из его углов находится в начале координат, а рёбра направлены вдоль координатных осей.
Тогда на плоскости координаты вершин квадратика — (0,0), (0,1), (1,0) и (1,1). А как устроены рёбра, то есть стороны квадрата? У каждого одна координата равна чему-то определённому — или 0, или 1, а другая меняется от 0 до 1, когда мы вдоль ребра идём.
В трёхмерном пространстве координаты всех вершин такого кубика — тоже нули или единицы; найдите на рисунке 7, например, вершину (0,0,1) или (1,1,0).
А рёбра? У каждого ребра какие-то две из трёх координат «закреплены», а третья в одном его конце равна 0 и ползёт от 0 до 1 по мере движения по ребру к другому концу. Так что задать (указать) ребро — это назвать две его «неподвижные» координаты. С гра нями похожая история, но теперь уже две координаты «бегают, как хотят» в пределах от 0 до 1, и только одна закреплена. Например, у передней грани куба на рисунке 7 координата y равна нулю. А у верхней — z=1.
В четырёхмерном пространстве у каждой точки 4 координаты, (x,y,z,u). У каждой вершины куба каждая координата равна 0 или 1. У каждого ребра снова может «бегать», изменяться лишь одна координата, а остальные — теперь уже три — закреплены. У грани закреплены 2 координаты, а у 3-грани — всего одна.
Сколько всего вершин? — а столько, сколько разных четвёрок можно составить из цифр 0 и 1! А 3-граней? — столько, сколько есть способов выбрать одну из четырёх координат и дать ей значение 0 или 1, тo есть 4 ∙ 2 = 8.
А рёбер сколько? Столько, сколько есть способов убрать одну лишнюю «бегающую» координату, да умножить на число троек из цифр 0 и 1, то есть 4∙(2∙2∙2)=32. Посчитать двумерные грани опять оставляем вам.
Конец решения задачи 0.
Вот ещё задачка, которую можно решить, помня об аналогии с рисованием 3-мерного кубика в двумерье:
Подсказка. Для четырёхмерных существ 3-кубик виден целиком, сразу со всех сторон. Так же, как мы из своего трёхмерья сразу целиком видим квадрат.
Решение этой задачи обсудим в следующем номере.
Художник Мария Усеинова.
Ответ к задаче 0
Двумерных граней 24.
Решение задачи 1
В каждом ребре (например, красном на рисунке) сходятся 3 двумерные грани (красная, жёлтая и фиолетовая), в каждой вершине (жирная точка) — 6 (добавляем три сине-зелёные грани). А трёхмерных граней в каждой вершине сходится 4, они «натянуты» на каждые 3 из четырёх выходящих из вершины рёбер. На втором рисунке они разнесены для наглядности; в исходном кубе они касаются двумерными гранями, так что отмеченные красные точки — их общая вершина — сливаются воедино.
Решение задачи 2
Выберем, например, боковую грань 3-кубика с чёрными рёбрами. Ей параллельны ещё одна грань того же 3-куба и две грани «синего». Всего — 4 параллельные грани в каждом направлении. А 3-грань, параллельная данной, одна.
Решение задачи 3
Через каждую вершину проходит ровно одна грань, параллельная данной. Перечислив все грани с данной вершиной (в задаче 1), мы решили и эту задачу.
Решение задачи 4
Как устроено изображение трёхмерного куба? У куба есть ближняя поверхность, которую мы видим, и дальняя, скрытая от взора (см. рисунок). Каждая из них состоит из трёх квадратов (на рисунке — параллелограммов), сходящихся в одной вершине (соответственно, ближней или дальней). Также и с 4-кубом: у него (для наблюдателя в 4-мерии) есть ближняя поверхность из всех четырёх кубов (на рисунке — параллелепипедов), сходящихся в одной вершине А, — эту картину мы видели в конце задачи 1 — и дальняя, из четырёх кубов-параллелепипедов у дальней вершины.
Чтобы найти невидимые рёбра, нужно выбрать, какая вершина будет дальней (из тех, что во внутренности рисунка), и исходящие из неё 4 ребра будут невидимы.
Ответы к упражнениям 1-3
Упражнение 1. а) Нет, у точек, лежащих на одном ребре, совпадают две из трёх координат; б) Ответ тривиальный — ребром, у которого x=1, z=0, оно параллельно оси y.
Упражнение 2. а) — в) Красная и зелёная точки, фиолетовое ребро и розовая грань на левом рисунке; г) жёлтая грань на правом рисунке.
Упражнение 3. z=1.
Как собрать кубик Рубика 3х3 — самый простой способ с видео без формул
Схема реализована без формул, в виде простых рисунков, понятных начинающим.
По алгоритмам кубик Рубика 3х3 собирается за 45 минут человеком, который ни разу не держал в руках кубик Рубика.
Скачать и распечатать схему вы можете кликнув на картинку ниже
Скачать схему сборки кубика Рубика 3х3 (формат pdf)
Также мы высылаем схему сборки кубика Рубика 3х3 с любым заказом, просто добавьте её в корзину!
Либо приступайте к обучению сразу на этой странице.
Сборка кубика Рубика в 8 этапов без формул
При сборке кубика Рубика 3х3 данным способом очень важно держать правильно кубик:
— до 8-го этапа кубик держим положением желтый центр сверху;
— при выполнении схем кубик не переворачиваем (не перехватываем)!
Желтый цвет всегда сверху — правильно
Желтый справа — не правильно
Желтый спереди — не правильно
Смотреть видео
1. Этап. Собираем «Ромашку» (белые ребра вокруг желтого центра)
1.1. Для постановки ребра на место, просто поверните соответствующую грань.
1
2
1
2
Смотреть видео
Если белое ребро сверху «мешает» установке другого белого ребра, отводим первое влево или вправо и выполняем соответствующий пункт 1.1.
1
2
Смотреть видео
При положении белого ребра сверху или снизу как на рисунках, выполняем соответствующие формулы, чтобы привести положение ребра к позиции 1.
1.
1
2
Смотреть видео
При положении ребра как в случае на рисунке ниже — выполните соответствующую схему
1
1
Смотреть видео
Повторяем подходящие схемы, пока не соберется «Ромашка».
Ромашка собрана!
Смотреть видео
2. Этап. Собираем белый крест внизу
Для установки ребра на место Поворачивая верхний слой, подводим ребро к своему цвету, и опускаем его вниз, поворачивая правую грань на 180 градусов
1
2
Смотреть видео
Повторяем схему выше для остальных цветов (зеленый, красный, оранжевый). В результате на белой стороне собирается правильный белый крест, а белые ребра креста стоят на своих местах
Белый крест собран!
Смотреть видео
3 этап. Собираем углы на белой стороне
На верхнем слое ищем угол с белым цветом и подоводим его к своему цвету, расположив в правой ближней стороне
Бело-сине-красный угол нужно поставить между красной и синей сторонами
Смотреть видео
Для того чтобы опустить угол на свое место, выполняем схему Пиф-Паф 1, 3, или 5 раз в зависимости от положения белого цвета в уголке.
(Схема Пиф-Паф — схема из четырех ходов, которую желательно выучить в первую очередь, так как она часто встречается в сборке кубика Рубика).
1. Белый справа
2. Белый сверху
3. Белый спереди
1
Схема Пиф-Паф 1 раз
2
Схема Пиф-Паф 3 раза
3
Схема Пиф-Паф 5 раз
Смотреть видео
Если угол с белым цветом находится внизу не на своем месте, “выгоняем” его наверх схемой Пиф-Паф и ставим на место согласно пункта 3
Схема Пиф-Паф 1 раз
Смотреть видео
Повторяем пункт 3 до тех пор, пока не соберем все белые уголки.
Нижний слой собран!
Смотреть видео
4 этап.
Собираем средний слойВ верхнем слое ищем ребра без желтого цвета, одно из них подводим под цвет своей боковой стороны
Смотреть видео
Если ребро должно уйти вправо, применяем схему 1 из 8-ми ходов ниже
Если ребро должно уйти влево, применяем схему 2 из 8-ми ходов ниже
1
2
Смотреть видео
Если какое-либо ребро без желтого цвета стоит в среднем слое не на своем месте, «выгоняем» его на верхний слой одной из предыдущих схем и повторяем п.4
1
2
Смотреть видео
5 этап. Собираем желтый крест
На данном этапе на верхнем слое выпадает один из трех вариантов (палка, бумеранг или площадка):
Палка
Бумеранг
Площадка
Смотреть видео
5.1. Если выпала палка — поворачиваем переднюю грань по часовой стрелке, выполняем схему Пиф-Паф 1 раз, поворачиваем переднюю грань против часовой стрелки — получаем желтый крест
5.
1. Палка
5.1.
Пиф-Паф 1 раз
Смотреть видео
5.2. Если выпал бумеранг — поворачиваем переднюю грань по часовой стрелке, выполняем схему Пиф-Паф 2 раза, поворачиваем переднюю грань против часовой стрелки — получаем желтый крест
5.2. Бумеранг
5.2
Пиф-Паф 2 раза
Смотреть видео
5.3. Если выпала площадка — поворачиваем переднюю грань по часовой стрелке, выполняем схему Пиф-Паф 1 раз, поворачиваем переднюю грань против часовой стрелки — получаем бумеранг, переходим к пункту 5.2.
5.3. Площадка
5.3
Пиф-Паф 1 раз
Смотреть видео
6 этап. Ставим на место желтные ребра
6.1. Поворачивая верхний слой вправо или влево, одно из рёбер верхнего слоя ставим на свое место и перехватываем кубик этим ребром к себе
Смотреть видео
Анализируем ситуацию с остальным желтыми ребрами.
Может выпасть 3 варианта:
1. Одно ребро совпадает, остальные не совпадают
2. Два соседних ребра совпадают, два других не совпадают
3. Два противоположных ребра совпадают, два других не совпадают.
В первом случае повторяем схему до тех пор, пока все ребра не встанут на свои места.
Во втором случае повторяем предыдущий шаг 6.1., но для совпадения ищем уже ребро другого цвета, чтобы привести положение ребер к варианту 1,
далее выполняем формулу до тех пор пока остальные ребра не встанут на свои места.
В третьем случае, выполняем схему, и переходим на предыдущий шаг 6.1.
Смотреть видео
Желтые ребра стоят на своих местах.
Желтный крест собран!
Смотреть видео
7 этап. Ставим углы на верхенем слое на свои места
Осматриваем углы.
Углы могут быть развернуты (желтый цвет не сверху), на это не обращаем внимания.
7.1. Если ни один из углов не стоит на своем месте, применяем схему, после чего как минимум один угол должен встать на свое место.
Переходим к шагу 7.2.
7.2. Если один из углов стоит на своем месте, а остальные нет, располагаем его в правой верней части перед собой
и применяем формулу сборки остальных углов (1 или 2 раза) до тех пор пока остальные углы не встанут на свои места
1
2
Смотреть видео
8 этап. Разворот углов (ставим желтые цвета углов к своей стороне)
8.1. Перехватываем кубик желтой гранью слева
Один из несобранных уголков располагаем слева сзади сверху
В зависимости от положения желтого цвета на данном уголке (сзади или сверху), выполняем схему Пиф-Паф 2 или 4 раза
Если желтый цвет уголка находится сзади, выполняем схему Пиф-Паф 2 раза
Если желтый цвет уголка находится сверху, выполняем схему Пиф-Паф 4 раза
1
2
1
Схема Пиф-Паф 2 раза
2
Схема Пиф-Паф 4 раза
Смотреть видео
8.
2. Разворот следующих неразвернутых углов
Не смотря на то, что все другие слои разберуться, кубик держим также и не перехватываем!!!
Поворачиваем левую грань до тех пор пока следующий несобраный угол не встанет в заднюю верхнюю левую часть и повторяем пункт 8.1 (кубик держим также и не перехватываем)
Если желтый собран — доворачиваем левую грань до правильного положения.
Кубик собран!
Шаблоны и алгоритмы кубика Рубика 4×4
С самого начала кубирования нам нравились узоры по ряду причин, включая их предсказуемость, эстетически приятные особенности и их адаптивность.
[скрыть]
[показать]
Содержание
- 1. Алгоритмы
- 2. Как сделать свои собственные выкройки
- 3. Создание кубов с помощью Cube Solver
- 4. Обратный алгоритм
- 5. Как читать обозначение
- 6. Примеры
Как сделать свои собственные выкройки
Паттерны почти безграничны, даже в большей степени на 4×4, чем на 3×3, в основном из-за четности и перемещений срезов.
Поскольку они являются разновидностью искусства, один кубер может думать, что это выглядит плохо, а другой может думать, что это красиво. Чтобы сделать свой собственный, я обычно просто играю с кубом. Однако вы также можете начать с существующего шаблона, а затем внести в него некоторые изменения, используя алгоритмы, отражающие переключатели, например M2 U2 M2 U2.
Большинство шаблонов имеют тенденцию отражать друг друга, поэтому четность OLL не будет играть огромной роли в создании шаблонов, но стоит упомянуть четность PLL. Тот факт, что у 4×4 есть эти паритеты, облегчает создание шаблонов, так как у вас больше свободы. В некоторых проектах четность используется для отражения только по одной оси или слою.
Конечно, вы также захотите отменить шаблоны. Для этого можно либо просто решить куб в обычном режиме, либо отменить алгоритм. Последний вариант рекомендуется, так как он, как правило, быстрее, чем обычное решение куба, особенно для более коротких алгоритмов, таких как простая шахматная доска [изображение]:
М2 Е2 С2.
Создание кубов с помощью Cube Solver
Создайте и визуализируйте 29 паттернов с помощью онлайн-решателя кубика Рубика. Эти конструкции подходят для любого куба-головоломки NxNxN, а не только для 4×4. Откройте Cube-Solver.com и выберите размер куба, чтобы начать работу, затем выберите пункт меню «Шаблоны». Вы увидите перечисленные имена:
Анаконда, Крест, Куб x2, Куб x4, Перекрученный куб x4, Шахматная доска, Шахматная доска1, Шахматная доска в кубе, Угловая пирамида, Смещенный мотив, Обмен утиными лапками, Четыре креста, Подарочная коробка, Перпендикулярные линии, Пираминкс, Питон, Шесть точек, Six Spots + Cross, Six-Two-One, Spiral, Staircase, Twin Peaks, Twister, Union Jack, Vertical Stripes, Viaduct, Weirdo, Wrapped 2×2, Yin Yang
Выберите имя для отображения алгоритма скремблирования. Вы можете щелкать по шагам, следуя поворотам.
Обратный алгоритм
Иногда может быть довольно сложно отменить паттерн, так как все ходы должны быть обратными .
Например, алгоритм
F L F U’ R U F2 L2 U’ L’ B D’ B’ L2 U
необходимо преобразовать в
U’ L2 B D B’ L U L2 F2 U’ R’ U F’ L’ F’
Как видите, сам алгоритм обратный, т.е. вы начинаете с конца, и ходы обратные; U становится U’ , U’ становится U , а технически U2 становится U2′
, но поскольку они одинаково влияют на куб, их не нужно менять местами. Перемещения фрагментов, такие как r2 или r’ , остаются с правой стороны, они просто меняются местами так же, как повороты внешнего слоя.Как читать обозначения
Нотация 4×4 основана на нотации 3×3. Обычные движения 3×3 U D R L F B M S E
— это тот же внешний слой, что и в 4×4.
Строчная буква , такая как r или u , означает, что вы перемещаете внутренний слой этой стороны.
Например, перемещение r’ означает, что вы перемещаете внутренний правый слой в том же направлении, что и R’, то есть вниз.
Ходы M, S и E никогда не пишутся строчными буквами, поскольку нет сторон или секторов, к которым они могли бы относиться, по крайней мере, не на 4×4.
Есть еще один тип движения, который используется на 4×4, и это широких хода или двухслойные перемещения. Эти ходы Uw, Dw, Rw, Lw, Fw и Bw .
Эти ходы идут в том же направлении, что и неширокие ходы: Rw идет в том же направлении, что и R, а Rw’ идет в том же направлении, что и R’. Это внешний слой и слой среза на этой стороне.
Подробнее о расширенной нотации читайте здесь.
Примеры
Маленькая коробка Большая коробка
B’ U’ B’ L’ D B U D2 B U L D’ L’ U’ L2 D
Угловая обертка
L U B’ U’ R L’ B R’ F B’ D R D’ F’
3×3 in 4×4
F L F U’ R U F2 L2 U’ L’ B D’ B’ L2 U
Bw2 Rw’ Dw Rw Dw’ Rw’ Dw Rw Uw
Rw’ Dw’ Rw Dw Rw’ Dw’ Rw Uw’ Bw2
Кольца
B’ M2 U2 M2 B F2 R U’ R U R2 R 2
F’ U F’ Uw Lw Uw’ Fw2
Dw Rw’ Uw Fw Dw2 Rw2
Комментарии
узоров извилистых головоломок — Ruwix
Я выделил отдельную страницу, чтобы перечислить самые красивые схемы кубика Рубика и их алгоритмы, чтобы помочь вам воспроизвести их самостоятельно.
Переходя к другим запутанным головоломкам, мы можем открыть новые измерения и дать волю своему воображению еще шире. В этой галерее я представляю несколько идей о том, как создавать потрясающие узоры на пазлах различной формы. В этом случае я приведу вам только один или два примера каждого куба, что позволит вам разобраться в алгоритмах и придумать еще более удивительные схемы.
Как правильно поздравить с днем рождения. Кубическая мозаика, построенная из различных головоломок NxNxN.
Прокрутите вниз, чтобы увидеть галерею.
Даже младшего брата Magic Cube 2×2 достаточно, чтобы сформировать красивый узор. Найдите алгоритмы этих милых мотивов на странице о Pocket Cube.
~
Мы пропустили Кубик Рубика, потому что у нас есть для него отдельная страница, а здесь полосатая Месть Рубика.
~
Профессорский куб имеет красивый спиральный дизайн. Этот вариант отлично смотрится и на больших головоломках NxNxN.
~
Вероятно, самые популярные модели головоломок — это змей , где непрерывная линия проходит вокруг головоломки, делая один или несколько поворотов на каждой грани.
С правой стороны вы можете увидеть «8 кубов пустоты».
~
Подарочная упаковка и еще одна спираль на большом кубе 7х7х7.
~
Нам достаточно сетки 7х7, чтобы нарисовать голову Супер Марио.
~
Комбинация «Шахматная доска» и «Кубик в кубе» на кубе 9×9.
~
На большом кубике 13x13x13 мы можем сделать красивую мозаику из кубика Рубика.
RedKB объясняет в видео на YouTube, как создать мозаику на каждой грани большого куба NxNxN.
Так выглядит SuperFlip на кубе 13x13x13.
~
Зеркальный куб — это модификация кубика Рубика, поэтому к нему можно применить любой алгоритм 3x3x3.
Вот как выглядит шаблон Python.
~
Другим популярным модом формы является Mastermorphix, где вы можете изобретать отличные скульптуры или схемы, если у вас есть один с цветными наклейками.
~
Выкройка скатерти на Мастерморфиксе 5x5x5.
~
Драгоценный камень на осевом кубе, еще один мод 3х3.
~
Цветочная модель отлично смотрится на Пираминксе.
Попробуйте перевернутые грани: F L U’ F L U’ F L U’ и шахматную доску: F U F L’ R U’ F L R’ ~
Знак плюс на головоломке Square-1.
~
Мастер Киломинкс со змеей.
~
Кубик Рубика в форме додекаэдра представляет собой Мегаминкс, вокруг которого обвивается змея.
~
Гигаминкс в шахматной доске.
~
Чтобы покрыть Тераминкс, нужна довольно большая змея.
~
Мартенс — самая длинная рептилия в нашем списке, она обвивается вокруг петаминкса. Я не смог найти изображение со змеей на Yottaminx, но я буду более чем счастлив опубликовать его, если вы пришлете мне его.
~
Узор в шахматном порядке на 30-цветной бумаге Petaminx.
~
Головоломка «Хрустальная пирамида» с цветочными узорами выглядит потрясающе.
~
«Треугольник в треугольнике» и «два глаза» на Rex Cube.
~
Кубовидные компенсационные кольца 5x5x4.
~
Крест на кубике 3x3x4.
~
Круги на Gear Cube Дэвида.
~
Шахматная доска на Gear Cube.
~
Блоки на вертолетном кубе.
~
Головоломка Dayan Gem.
~
Шахматная доска на Master Skewb.
~
Обмен центрами на Решетчатом кубе Окамото и Грега.
~
Четыре точки на квадратном кубе.
~
Два экземпляра Curvy Copter Skewb.
~
6 точек на кубике мозаики.
~
Магический октаэдр.
~
Шестиугольная призма.
~
Октаэдр 4×4.
~
Химера 2х2+6х6 (перевязанная 6х6х6).
~
Круги на Crazy i-Cube 3x3x4.
~
Безумные схемы 3х3х3 Плюс.
~
Перевязанный кубик-головоломка Real Bi-5.
~
Блок-защелка.
~
Крест на кубе Mixup Plus 3x3x3
~
Безумный тетраэдр.
~
Куб Master Mixup, перевязанный клетчатой лентой.
~
Leave a Comment