Куб черчение: Как нарисовать куб в перспективе за 15 шагов

25.04.2023 Facebook Twitter LinkedIn Google+ Разное

Содержание

Куб карандашом поэтапно — 71 фото

Рисуем куб карандашом поэтапно для начинающих


Поэтапное рисование Куба


Куб в перспективе и сбоку


Поэтапное рисование Куба


Построение гипсового Куба


Рисование объемных фигур куб


Куб в перспективе


Как нарисовать куб карандашом поэтапно


Куб в перспективе со штриховкой


Гипсовый куб в перспективе


Объёмные фигуры с разных ракурсов


Объемные квадраты для рисования


Рисунок Куба


Линейно конструктивное построение Куба


Штриховка Куба Академ


Параллелепипед карандашом


Куб объемный карандашом без теней


Нарисуйте куб


Куб карандашом


Зарисовки геометрических тел


Поэтапное рисование Куба


Нарисовать куб карандашом


Объемный куб с тенью


Композиция из кубов в перспективе


Построение Куба


Рисование Куба в перспективе


Объемный квадрат


Геометрические фигуры рисунок


Объемный куб


Академическое построение Куба


Рисованиегеометрических фигуор


Как нарисовать Тадароки поэтапно


Рисование Куба в перспективе


Линейная перспектива с 2 точками схода


Угловая перспектива( двухточечная линейная перспектива)


Куб с тенью


Шестигранная Призма цилиндр куб


Карандашный стул фото


Одноточечная и линейная перспектива


Невозможный куб Эшера


Рисунки по этапам


Геометрические фигуры срисовать


Рисование объемных фигур куб


Геометрический натюрморт


Рисованиегеометрических фигуор


Рисование с натуры геометрических тел


Кубик Рубика карандашом


Куб Геометрическая фигура


Объемный квадрат


Куб черчение


Линейно конструктивное построение шара


Рисование геометрических тел (Призма, пирамида, куб).


Академическая штриховка шара


Рисование геометрических тел (Призма, пирамида, куб).


Схематичный куб


Аспекты кубов Неккера


Шар карандашом


Изображение Куба


Линейно-конструктивное построение натюрморта


Поэтапное рисование шара


Объемные оптические иллюзии


Конус рисунок


Натюрморт фигуры


Куб гексаэдр


Рисование коробки поэтапно


Геометрические фигуры в перспективе


Уроки скетчинга для начинающих


Подарок рисунок карандашом


Чертеж квадрата в объеме


Необычные геометрические фигуры


Рисование геометрических фигур карандашом

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе

Гости, не могут оставлять комментарии к данной публикации.

Построение изометрической и диметрической проекций окружностей, расположенных в плоскостях, параллельных плоскостям проекций

Непосредственное проектирование окружности на плоскость можно заменить проектированием описанного вокруг неё квадрата с последующим вписанием в проекцию квадрата проекции окружности. При этом используются следующие свойства параллельного проектирования этих фигур: 1) точка пересечения диагоналей проекции квадрата есть центр проекции окружности; 2) точками касания проекции окружности к проекции квадрата остаются средние точки сторон проекции квадрата; 3) на­правление сторон проекции квадрата является направлением двух сопряжённых диаметров проекции окружности.

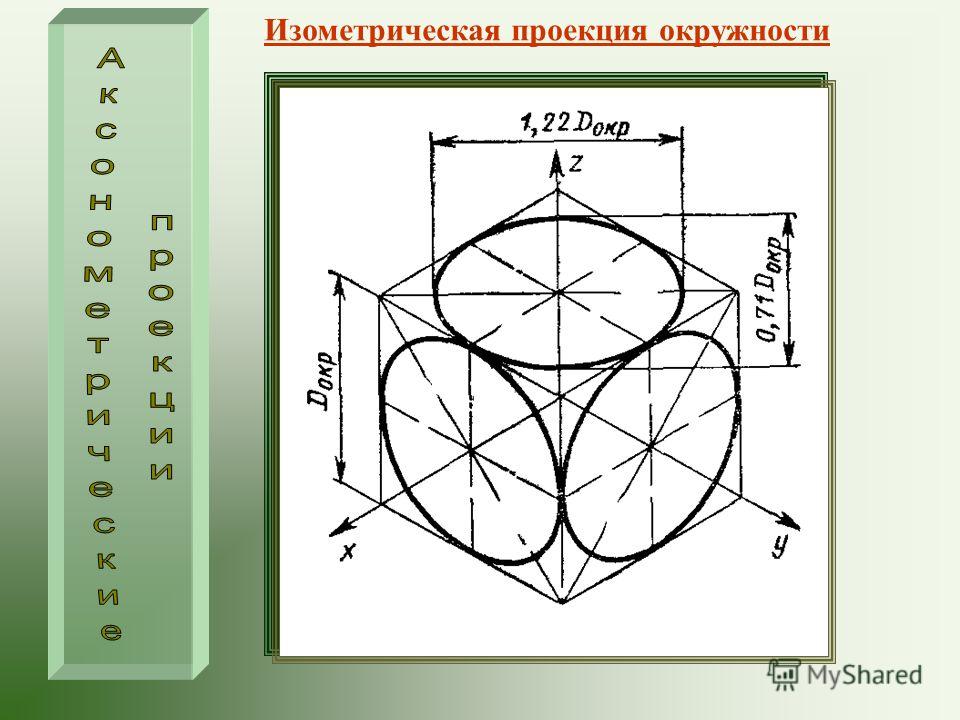
Построим изометрическую проекцию окружности, лежащей в какой- нибудь координатной плоскости. Для этого возьмём куб, в грани которого впишем окружности. Куб расположим так, чтобы его грани были параллельны координатным плоскостям (фиг. 189).

Проекция куба имеет форму правильного шестиугольника, а проекцией каждой его грани является ромб.

Равенство ромбов—проекций квадратов—предопределяет и равенство эллипсов—проекций, вписанных в грани куба окружностей. Направления главных осей эллипса в изометрических проекциях совпадают с диагоналями ромба, в который вписан эллипс.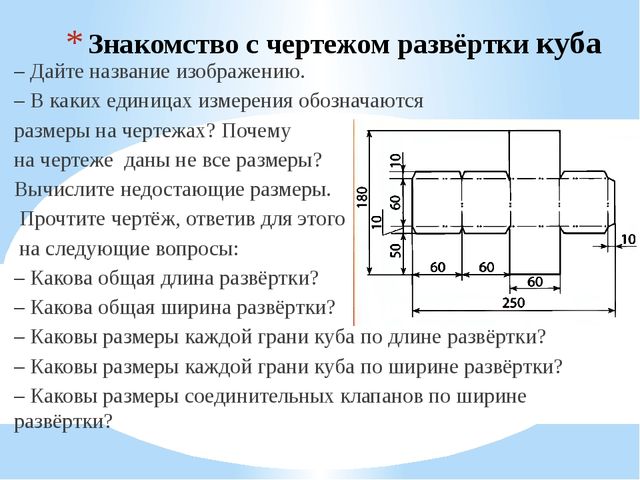

Следует запомнить простое правило нахождения большой и малой осей: малая ось всегда параллельна той оси, которой нет в названии плоскости эллипса. Так, например, если для эллипса плоскости OXZ нет названия оси OY, то малая ось этого эллипса параллельна оси OY. Большая ось всегда перпендикулярна к малой.

Можно это же условие выразить иначе: малая ось эллипса совпадает по направлению либо параллельна перпендикуляру к плоскости, в которой лежит спроектированная в эллипс окружность.

Чтобы построить эллипс по главным его осям, кроме направления, необходимы и размеры этих осей.

Как известно, независимо от положения плоскости проекций, большая ось эллипса всегда равна величине диаметра окружности, а малая в изометрической проекции равна 0,58 диаметра окружности. Прибли­жённо можно принять отношение между осями эллипса, равным 3:5.

Если построение окружности выполняется в масштабе 1,22:1, то при построении большой оси надо взять 1,22 d, а для малой 3/5 этой вели­чины, т. е. 0,725 d.

В практике часто вместо построения эллипсов лекальные кривые за­меняют циркульными и строят овал с тем же отношением 3:5 между главными осями.

На фиг. 189,б и в приведён способ построения овалов, заменяющих вписанные эллипсы. На одном чертеже овал вписан в ромб, соответ­ствующий горизонтальной грани куба, а на втором—двум боковым граням.

На фиг. 190 дана диметрическая прямоугольная проекция окруж­ности. Свойства, перечисленные в предыдущем случае, остаются в силе и здесь.

Эллипс, в который проектируется окружность, лежащая на передней грани куба, имеет, как и в случае изометрических проекций, главные оси, сливающиеся с диагоналями куба. Конечные точки осей могут быть определены как точки, делящие каждую из полудиагоналей ромба на части в отношении 7:10.

Для боковой грани и для грани верхнего основания куба направление малой оси эллипса параллельно аксонометриче­ской оси OY. Зная направление малых осей эллипсов, легко определить направление больших осей.

Для боковой грани боль­шая ось наклонена к оси OZ на угол 7°, а для грани верх­него основания большая ось будет горизонтальной прямой.

При проектировании в масштабе 1,06:1 длина боль­шой оси эллипса равна 1,06 d, где d  — диаметр окружности.

Что касается малой оси, то для фронтальной грани она равна 0,89, т. е. около 0,9 большой оси. Для граней бо­ковой и горизонтальной малая ось принимается равной 0,35 ребра куба или 1/3 большой оси эллипса.

Практически в этом слу­чае вместо эллипсов можно строить овалы.

На фиг. 190, б и в пока­заны способы построения ова­лов для каждой грани от­дельно.

И, наконец, при косо­угольном проектировании диметрическая проекция фрон­тальной грани куба проекти­руется без искажений; очевидно, и окружность, вписанная в эту грань, проектируется в окружность (фиг. 191, а и в).

Боковая грань и грань верхнего основания куба по­чти не отличаются по форме от соответствующих граней, построенных в прямоугольной проекции.

Овалы в этом случае вычерчиваются почти так же, как и на соот­ветственных гранях куба предыдущего случая.

Как нарисовать невозможный куб

2,4 тыс. акций

Узнайте, как нарисовать великолепный рисунок Невозможный куб с помощью пошаговых инструкций и видеоуроков.

Следуя простым шагам, вы тоже сможете легко нарисовать красивый Невозможный Куб.

Перейти к пошаговым инструкциям.

Полный чертеж невозможного куба

Что такое невозможный куб? Эта оптическая иллюзия, также называемая иррациональным кубом, была создана голландским художником М. К. Эшером в 1958. На его литографии Belvedere изображено здание, основанное на невозможном кубе, которое, кажется, бросает вызов законам геометрии.

Невозможный куб определяется как «двумерная фигура, внешне напоминающая перспективный рисунок трехмерного куба, с чертами, нарисованными непоследовательно по сравнению с тем, как они выглядели бы в реальном кубе».

Другими словами, изображение выглядит как куб, который соединяется и перекрывается невозможным образом.

Прокрутите вниз, чтобы загрузить PDF-файл этого руководства.

Невозможный куб связан с кубом Неккера — линейным рисунком, на котором передняя грань куба может выглядеть как один из двух разных квадратов, в зависимости от того, как вы на это смотрите.

Верхние пересечения лучей невозможного куба напоминают одну ориентацию куба Неккера, а нижние пересечения — другую. В результате получается кажущийся трехмерным объект, который не мог бы существовать в реальной жизни.

Многие художники экспериментировали с невозможным кубом, часто для создания занимательных оптических иллюзий. Некоторые статуи даже подходят под это описание, если смотреть на них под определенным углом.

В 1966 году в журнале Scientific American была опубликована фотография, на которой изображен невозможный куб.

Как работают подобные оптические иллюзии? Человеческий глаз имеет тенденцию воспринимать двухмерные рисунки как трехмерные объекты. Поэтому линии на бумаге кажутся реальным осязаемым объектом.

Иллюзии также опираются на то, что мы уже знаем о мире. Наш глаз можно обмануть, заставив применить к изображению общую геометрию или размеры. В случае невозможного куба мы делаем предположения о прямых углах и прочности балок.

Хотите нарисовать невозможный куб? Этот простой пошаговый учебник по рисованию куба здесь, чтобы помочь. Все, что вам понадобится, это карандаш, лист бумаги и ластик. Вы также можете раскрасить готовый рисунок.

Если вам понравился этот урок, см. Также следующие руководства по рисованию: Бейсбол, Футбол и Футбольный шлем.

​Пошаговые инструкции по рисованию​ невозможного куба

Как нарисовать великолепный невозможный куб для детей, начинающих и взрослых. Шаг 1

1. Начните с рисования трех прямых вертикальных линий. Линии должны быть одинаковой длины, но средняя линия должна располагаться ниже остальных. Затем соедините линии внизу прямыми линиями. Это формирует боковые и нижние грани куба.

Простое рисование невозможного куба — Шаг 2

2. Нарисуйте четырехугольник или четырехугольник на вершине куба.

Легкий и невозможный рисунок куба. Шаг 3

3. Затем детализируйте верхнюю панель куба. Нарисуйте меньший квадрат внутри верхней стороны куба. Вытяните короткую прямую линию из самого верхнего угла этого квадрата. Затем нарисуйте две прямые линии, отходящие от этой линии, параллельно сторонам квадрата.

Легко невозможное рисование куба – шаг 4

4. Нарисуйте квадрат внутри одной из боковых панелей куба.

Легко невозможное рисование куба – Шаг 5

5. Нарисуйте квадрат внутри оставшейся боковой панели куба.

Простое рисование невозможного куба. Шаг 6

6. Нарисуйте короткие прямые линии, идущие от противоположных углов квадратов. Затем нарисуйте две прямые линии, отходящие от каждой из коротких линий. Эти линии должны быть параллельны сторонам квадрата.

Простое рисование невозможного куба.

Шаг 7

7. Протяните три прямые линии из нижнего левого угла куба. Затем вытяните три прямые линии из нижнего правого угла куба. Позвольте нижней и средней линиям встретиться. Затем соедините концы линий, образуя прямоугольники.

Добавьте больше деталей к рисунку невозможного куба – шаг 8

8. Сотрите направляющие линии с фигур, нарисованных на предыдущем шаге

Завершите контур вашего рисунка невозможного куба – шаг 9 невозможный куб. Нарисуйте три прямые параллельные линии, соединяющие верхний и нижний задние углы куба.

Раскрась свой невозможный куб Рисунок

10. Раскрась свой невозможный куб.

Ознакомьтесь с нашими руководствами по рисованию искусственных объектов, чтобы узнать больше.

Простое, пошаговое руководство по рисованию невозможного куба

Нажмите ЗДЕСЬ, чтобы сохранить урок в Pinterest!

Учебник по рисованию невозможного куба — легко и весело Страницы для печати

УСТРАНЕНИЕ НЕИСПРАВНОСТЕЙ ДЛЯ УЧАСТНИКОВ

Все еще видите рекламу или не можете загрузить PDF-файл?

Во-первых, убедитесь, что вы вошли в систему. Вы можете войти на странице входа участника.

Если вы по-прежнему не можете загрузить PDF-файл, вероятное решение — перезагрузить страницу.

Это можно сделать, нажав кнопку перезагрузки браузера.

Это значок в виде круглой стрелки в верхней части окна браузера, обычно расположенный в верхней левой части (вы также можете использовать сочетания клавиш: Ctrl+R на ПК и Command+R на Mac).

threed — рисование куба в ggplot2

Введение

В этом посте рассказывается, как построить куб в ggplot2 используя библиотеку threed .

ggplot2 не включает понятие 3-й пространственной оси, поэтому вместо этого после манипулируя 3D-объектом, мы используем перспективную проекцию, чтобы «сгладить» его грани и вершины на двумерную плоскость. Эти спроецированные грани/вершины — это то, что будет отображать ggplot2.

Подготовить объект для построения

  • Создать объект (здесь используется стандартный куб 2x2x2)
  • Определите, где находится камера и куда она смотрит
  • Превратить объект в пространство камеры
  • Перспективное преобразование данных
 #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Пакет `threed` имеет несколько встроенных объектов в `threed::mesh4dobj`
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
obj <- threed::mesh4dobj$cube
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Определить матрицу обзора камеры, т.
 
 е. преобразование камеры в мир
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
camera_to_world <- threed::look_at_matrix(eye = c(1.5, 1.75, 4), at = c(0, 0, 0))
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Трансформируем объект в пространство камеры и делаем перспективную проекцию
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
объект <- объект %>%
  transform_by (invert_matrix (camera_to_world)) %>%
  перспектива_проекция() 
 as.data.frame(obj) %>% Knitr::kable()
1 4 1 -0,0945866 -0,0706857 1,581399 1 -0,1855445 -0,1356142 -0,9732328 0,1523493 0,1540033 -0,9762544 0,0748818 0,0756647 1. 630932 1 1.630932 ИСТИНА
1 4 2 -0,1077957 0,2603509 1.631559 3 -0,2154400 -0,3088482 -0,9263900 0,1523493 0,1540033 -0,9762544 0,0748818 0,0756647 1.630932 1 1.630932 ИСТИНА
1 4 3 0,2693976 0,2400504 1.687219 4 -0,4345424 -0,3475777 -0,8308806 0,1523493 0,1540033 -0,9762544 0,0748818 0,0756647 1. 630932 1 1.630932 ИСТИНА
1 4 4 0,2325119 -0,1270569 1.623552 2 -0,3706042 -0,1407513 -0,9180640 0,1523493 0,1540033 -0,9762544 0,0748818 0,0756647 1.630932 1 1.630932 ИСТИНА
2 4 1 -0,1077957 0,2603509 1.631559 3 -0,2154400 -0,3088482 -0,9263900 0,0000000 0,9394660 0,3426420 0,0013440 0,2085811 1. 773502 5 1.773502 ЛОЖЬ
2 4 2 -0,3483420 0,16 1.823482 7 0,1812743 0,2777220 0,9434035 0,0000000 0,9394660 0,3426420 0,0013440 0,2085811 1.773502 5 1.773502 ЛОЖЬ
2 4 3 0,1921159 0,1435705 1,951750 8 -0,6699657 0,4605475 0,5822731 0,0000000 0,9394660 0,3426420 0,0013440 0,2085811 1. 773502 5 1.773502 ЛОЖЬ
2 4 4 0,2693976 0,2400504 1.687219 4 -0,4345424 -0,3475777 -0,8308806 0,0000000 0,9394660 0,3426420 0,0013440 0,2085811 1.773502 5 1.773502 ЛОЖЬ
3 4 1 0,2325119 -0,1270569 1.623552 2 -0,3706042 -0,1407513 -0,9180640 0,9631644 -0,1369155 0,2314485 0,2119637 -0,0287422 1. 767221 4 1.767221 ЛОЖЬ
3 4 2 0,2693976 0,2400504 1.687219 4 -0,4345424 -0,3475777 -0,8308806 0,9631644 -0,1369155 0,2314485 0,2119637 -0,0287422 1.767221 4 1.767221 ЛОЖЬ
3 4 3 0,1921159 0,1435705 1,951750 8 -0,6699657 0,4605475 0,5822731 0,9631644 -0,1369155 0,2314485 0,2119637 -0,0287422 1. 767221 4 1.767221 ЛОЖЬ
3 4 4 0,1538294 -0,3715328 1.806364 6 0,3411191 0,1021382 0,9344547 0,9631644 -0,1369155 0,2314485 0,2119637 -0,0287422 1.767221 4 1.767221 ЛОЖЬ
4 4 1 -0,0945866 -0,0706857 1,581399 1 -0,1855445 -0,1356142 -0,9732328 -0,6370835 0,05 -0,7654561 -0,2099435 0,0306140 1. 689395 3 1.689395 ИСТИНА
4 4 2 -0,28 -0,2575617 1.721140 5 -0,1542710 -0,1026941 -0,9826771 -0,6370835 0,05 -0,7654561 -0,2099435 0,0306140 1.689395 3 1.689395 ИСТИНА
4 4 3 -0,3483420 0,16 1.823482 7 0,1812743 0,2777220 0,9434035 -0,6370835 0,05 -0,7654561 -0,2099435 0,0306140 1.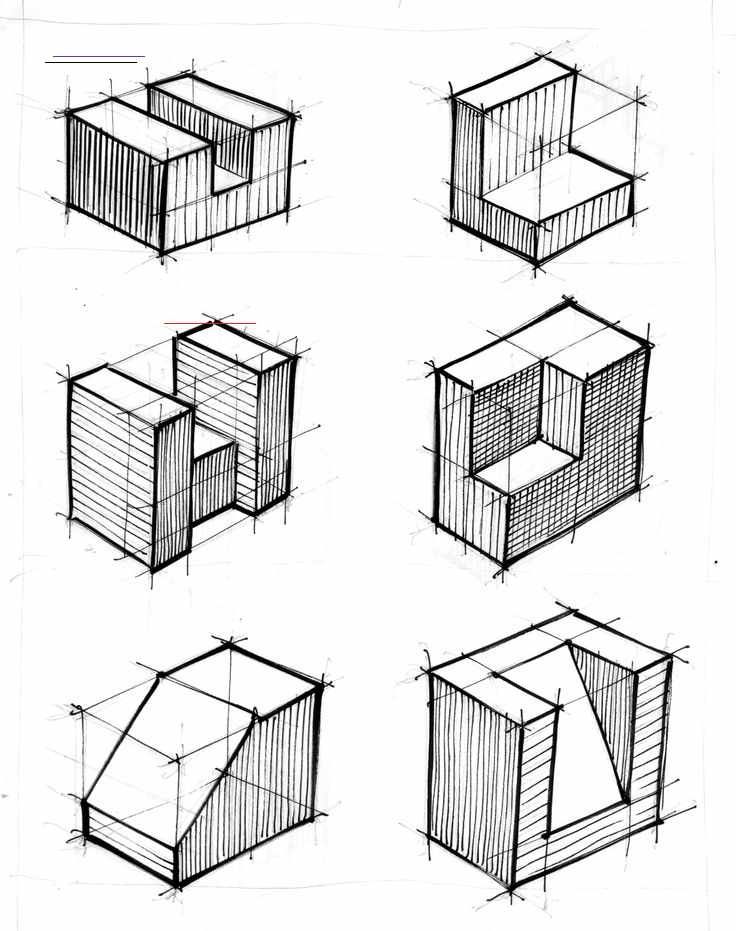 689395 3 1.689395 ИСТИНА
4 4 4 -0,1077957 0,2603509 1.631559 3 -0,2154400 -0,3088482 -0,9263900 -0,6370835 0,05 -0,7654561 -0,2099435 0,0306140 1.689395 3 1.689395 ИСТИНА
5 4 1 -0,0945866 -0,0706857 1,581399 1 -0,1855445 -0,1356142 -0,9732328 0,0000000 -0,5988573 -0,8008558 0,0006763 -0,2067093 1. 683114 2 1.683114 ИСТИНА
5 4 2 0,2325119 -0,1270569 1.623552 2 -0,3706042 -0,1407513 -0,9180640 0,0000000 -0,5988573 -0,8008558 0,0006763 -0,2067093 1.683114 2 1.683114 ИСТИНА
5 4 3 0,1538294 -0,3715328 1.806364 6 0,3411191 0,1021382 0,9344547 0,0000000 -0,5988573 -0,8008558 0,0006763 -0,2067093 1. 683114 2 1.683114 ИСТИНА
5 4 4 -0,28 -0,2575617 1.721140 5 -0,1542710 -0,1026941 -0,9826771 0,0000000 -0,5988573 -0,8008558 0,0006763 -0,2067093 1.683114 2 1.683114 ИСТИНА
6 4 1 -0,28 -0,2575617 1.721140 5 -0,1542710 -0,1026941 -0,9826771 -0,2439436 -0,2465920 0,9379147 -0,0728616 -0,0737928 1. 825684 6 1.825684 ЛОЖЬ
6 4 2 0,1538294 -0,3715328 1.806364 6 0,3411191 0,1021382 0,9344547 -0,2439436 -0,2465920 0,9379147 -0,0728616 -0,0737928 1.825684 6 1.825684 ЛОЖЬ
6 4 3 0,1921159 0,1435705 1,951750 8 -0,6699657 0,4605475 0,5822731 -0,2439436 -0,2465920 0,9379147 -0,0728616 -0,0737928 1. 825684 6 1.825684 ЛОЖЬ
6 4 4 -0,3483420 0,16 1.823482 7 0,1812743 0,2777220 0,9434035 -0,2439436 -0,2465920 0,9379147 -0,0728616 -0,0737928 1.825684 6 1.825684 ЛОЖЬ

Постройте точки для вершин объекта

  • threed определяет функцию fortify.mesh4d() .
  • Если объект mesh4d задан как данные для вызова ggplot2 , ggplot2 будет автоматически использовать fortify() для преобразования в data. frame.
  • , т. е. поскольку threed определяет fortify.mesh4d() , мы можем вызвать ggplot2 напрямую с объектом mesh4d .
 ggplot(obj, aes(x, y)) +
  геометрическая_точка() +
  тема_пусто() +
  тема (легенда.позиция = 'нет') +
  coord_equal()

Построить контур каждого полигона

  • Каждый элемент имеет уникальный element_id , и это используется как эстетика группы чтобы сообщить ggplot, что он должен рисовать один полигон для каждого элемента.
  • Установите fill = NA, color = 'black' , чтобы рисовать только границы каждого полигона.
 ggplot(obj, aes(x, y, group = element_id)) +
  geom_polygon (заливка = нет данных, цвет = «черный», размер = 0,2) +
  тема_пусто() +
  тема (легенда.позиция = 'нет') +
  coord_equal()

Точечная визуализация скрытых линий

  • Чтобы нарисовать скрытые элементы другим способом, используйте переменную hidden .
  • hidden — логическая переменная, указывающая, обращен ли треугольный или четырехугольный элемент подальше от камеры.
  • Здесь используется другой тип линии для скрытых элементов
 ggplot(obj, aes(x, y, group = element_id)) +
  geom_polygon (fill = NA, color = 'black', aes (linetype = hidden, size = hidden)) +
  scale_linetype_manual (значения = c («ИСТИНА» = «точечный», «ЛОЖЬ» = «сплошной»)) +
  scale_size_manual (значения = c («ИСТИНА» = 0,2, «ЛОЖЬ» = 0,5)) +
  тема_пусто() +
  тема (легенда.позиция = 'нет') +
  coord_equal()

Удаление скрытых линий

  • Здесь для скрытых элементов используется тип линии нулевой ширины .
 ggplot(obj, aes(x, y, group = element_id)) +
  geom_polygon (fill = NA, color = 'black', aes (size = hidden)) +
  scale_size_manual (значения = c («ИСТИНА» = 0, «ЛОЖЬ» = 0,5)) +
  тема_пусто() +
  тема (легенда.позиция = 'нет') +
  coord_equal()

Наивные заполненные полигоны

  • При заливке полигонов, ggplot2 отрисует их в порядке групповой переменной.
  • Если сгруппировать по element_id , то полигоны рисуются в том порядке, в котором они были определены. Это означает, что полигоны, которые находятся дальше, будут рисовать поверх тех, которые на самом деле близко к глазу.
  • Результат будет выглядеть странно — почти в стиле Эшера!
 ggplot(obj, aes(x, y, group = element_id)) +
  geom_polygon (заливка = «голубой», цвет = «черный», размер = 0,2) +
  тема_пусто() +
  тема (легенда.позиция = 'нет') +
  coord_equal()

Закрашенные многоугольники — (1) Удаление скрытых элементов, чтобы они никогда не отображались

  • Первый метод для рисования закрашенных многоугольников:
    • удалить скрытые элементы вручную
    • Сделайте это, явно преобразовав объект mesh4d в data.frame, а затем отфильтровав чтобы сохранить только те элементы, которые не скрыты.
  • Для объектов mesh4d , преобразованных в data. frames, скрытый определяется как ИСТИНА для любая грань, нормаль которой указывает на отрицательную ось Z (т. е. с плоскости просмотра).
 obj_df <- as.data.frame(obj) %>%
  фильтр(!скрытый)
ggplot (obj_df, aes (x, y, группа = element_id)) +
  geom_polygon (заливка = «голубой», цвет = «черный», размер = 0,2) +
  тема_пусто() +
  тема (легенда.позиция = 'нет') +
  coord_equal()

Закрашенные полигоны — (3) Используйте переменную

zorder для управления порядком прорисовки
  • Третий метод для рисования заполненных полигонов:
    • Нарисуйте элементы от самого дальнего к ближайшему
    • Используйте тот факт, что элементы рисуются в порядке групповой переменной.
    • При преобразовании mesh4d в data.frame создается переменная zorder , начиная с 1 для самого дальнего элемента, до n для ближайшего элемента.
Comments
Leave Comment