Куб черчение – 3 — () n- (3-n)

---

14.11.2019 Разное

---

Урок черчения «Геометрические тела. Комплексные чертежи многогранников»

Разделы: Технология

Класс:

---

Цели урока:

• закрепить знания о геометрических телах, умения и навыки по построению чертежей многогранников;
• развивать пространственные представления и пространственное мышление;
• формировать графическую культуру.

Тип урока: комбинированный.

Оснащение урока: интерактивная доска MIMIO, мультимедийный проектор, компьютеры, проект mimo для интерактивной доски, мультимедийная презентация, программа «Компас-3D LT».

ХОД УРОКА

I. Организационный момент

1. Приветствие;

2. Проверка явки учащихся;

3. Проверка готовности к уроку;

4. Заполнение классного журнала (и электронного)

II. Повторение раннее изученного материала

На интерактивной доске открыт проект mimo

Лист 1. На уроках математики вы изучали геометрические тела. Несколько тел вы видите на экране. Давайте вспомним их названия. Учащиеся дают названия геометрическим телам, если есть затруднения – помогаю. (Рис. 1).

Рис. 1

1 – четырехугольная призма
2 – усеченный конус
3 – треугольная призма
4 – цилиндр
5 – шестиугольная призма
6 – конус
7 – куб
8 – усеченная шестиугольная пирамида

Лист 4. Задание 2. Даны геометрические тела и названия геометрических тел. Вызываем ученика к доске и вместе с ним перетаскиваем многогранники и тела вращения под названия, а затем перетаскиваем названия геометрических тел (рис. 2).

Рис. 2

Делаем вывод, что все тела делятся на многогранники и тела вращения.

Включаем презентацию «Геометрические тела» (Приложение). Презентация содержит 17 слайдов. Можно использовать презентацию на нескольких уроках, она содержит дополнительный материал (слайды 14-17). Со слайда 8 есть гиперссылка на Презентацию 2 (развертки куба). Презентация 2 содержит 1 слайд, на котором изображены 11 разверток куба (они являются ссылками на видеоролики). На уроке использована интерактивная доска MIMIO, а также учащиеся работают на компьютерах (выполнение практической работы).

Слайд 2. Все геометрические тела делятся на многогранники и тела вращения. Многогранники: призма и пирамида. Тела вращения: цилиндр, конус, шар, тор. Схему учащиеся перечерчивают в рабочую тетрадь.

III. Объяснение нового материала

Слайд 3. Рассмотрим пирамиду. Записываем определение пирамиды. Вершина пирамиды – общая вершина всех граней, обозначается буквой S. Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды (Рис. 3).

Рис. 3

Слайд 4. Правильная пирамида. Если основание пирамиды — правильный многоугольник, а высота опускается в центр основания, то — пирамида правильная.
В правильной пирамиде все боковые ребра равны, все боковые грани равные равнобедренные треугольники.
Высота треугольника боковой грани правильной пирамиды называется — апофема правильной пирамиды.

Слайд 5. Анимация построения правильной шестиугольной пирамиды с обозначением ее основных элементов (Рис. 4).

Рис. 4

Слайд 6. Записываем в тетрадь определение призмы. Призма – многогранник, у которого два основания (равные, параллельно расположенные многоугольники), а боковые грани параллелограммы. Призма может быть четырехугольной, пятиугольной, шестиугольной и т.д. Призма называется по фигуре, лежащей в основании. Анимация построения правильной шестиугольной призмы с обозначением ее основных элементов (Рис. 5).

Рис.5

Слайд 7. Правильная призма – это прямая призма, в основании которой лежит правильный многоугольник. Параллелепипед – правильная четырехугольная призма (Рис. 6).

Рис. 6

Слайд 8. Куб – параллелепипед, все грани которого квадраты (Рис. 7).

Рис. 7

(Дополнительный материал: на слайде есть гиперссылка на презентацию с развертками куба, всего 11 разных разверток).
Слайд 9. Записываем определение цилиндра. Тело вращения – цилиндр, образованное вращением прямоугольника вокруг оси, проходящей через одну из его сторон. Анимация получения цилиндра (Рис. 8).

Рис. 8

Слайд 10. Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг оси, проходящей через один из его катетов (Рис.9).

Рис. 9

Слайд 11. Усеченный конус – тело вращения, образованное вращением прямоугольной трапеции вокруг оси, проходящей через ее высоту (Рис. 10).

Рис. 10

Слайд 12. Шар – тело вращения, образованное вращением круга вокруг оси, проходящей через его диаметр (Рис. 11).

Рис. 11

Слайд 13. Тор – тело вращения, образованное вращением круга вокруг оси, параллельной диаметру круга (Рис. 12).

Рис. 12

Учащиеся записывают определения геометрических тел в тетрадь.

IV. Практическая работа«Построение чертежа правильной призмы»

Переключаемся на проект mimio

Лист 7. Дана треугольная правильная призма. В основании лежит правильный треугольник. Высота призмы = 70 мм, а сторона основания = 40 мм. Рассматриваем призму (направление главного вида показано стрелкой), определяем плоские фигуры, который мы увидим на виде спереди, сверху и слева. Вытаскиваем изображения видов и расставляем на поле чертежа (Рис. 13).

Рис. 13

Учащиеся самостоятельно выполняют чертеж правильной шестиугольной призмы в программе «Компас – 3D». Размеры призмы: высота – 60 мм, диаметр описанной окружности вокруг основания – 50 мм.
Построение чертежа с вида сверху (Рис. 14).

Рис. 14

Затем строится вид спереди (Рис. 15).

Рис. 15

Затем строится вид слева и наносятся размеры (Рис. 16).

Рис. 16

Работы проверяются и сохраняются на компьютерах учащимися.

V. Дополнительный материал по теме

Слайд 14. Правильная усеченная пирамида (Рис. 17).

Рис. 17

Слайд 15. Пирамида, усеченная наклонной плоскостью (Рис. 18).

Рис. 18

Слайд 16. Развертка правильной треугольной пирамиды (Рис. 19).

Рис. 19

Слайд 17. Развертка параллелепипеда (Рис. 20).

Рис. 20

4.01.2012

urok.1sept.ru

ЧЕРЧЕНИЕ. Школьный интернет-учебник — Чтение чертежей 3-4

Многообразие геометрических форм

На уроках математики вы уже познакомились с некоторыми геометрическими фигурами. Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.

Если все точки фигуры лежат в одной плоскости, фигуру называют плоской: треугольник, квадрат и др. Совокупность точек, расположенных в пространстве, образует пространственную фигуру: куб, цилиндр и др. Фигуры в пространстве называют  геометрическими телами.

Предметы, которые нас окружают, детали машин имеют, как правило, сложную реальную геометрическую форму. Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются  призмы, пирамиды, цилиндры, конусы, шары и др. (рис. 1)

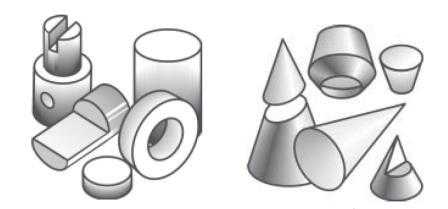
Рис. 1.  Геометрические тела

По форме простые геометрические тела делятся на многогранники и тела вращения. Плоскость является частным случаем поверхности.

Многогранники – геометрические тела, поверхность которых состоит из плоских многоугольников. Это куб, призма, параллелепипед, пирамида и др.

Тела вращения – геометрические тела, поверхность которых описывается какой-либо прямой или кривой (образующей) при её вращении вокруг неподвижной оси (например, конус, цилиндр, шар и т. п.).

Форма каждого геометрического тела имеет свои характерные признаки. По ним мы отличаем призму от цилиндра, пирамиду от конуса и  т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.

Поскольку форма большинства предметов представляет собой сочетание различных геометрических тел или их частей, для построения чертежей этих предметов необходимо знать, как изображается каждое геометрическое тело. Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.

Изображение многогранников

Рассмотрим построение прямоугольных проекций призмы. Для примера возьмем треугольную призму (рис. 2) и шестиугольную призму (рис. 3). Их основания, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых — на тех, которым перпендикулярны. Грани, наклонные к плоскостям, изображаются на них искаженными.

Рис. 2. Треугольная призма

Рис. 3. Шестиугольная призма.

Размеры призм определяются их высотами и размерами фигур основания. Штрихпунктирными линиями на чертеже изображаются оси симметрии.

Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рис. 4). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нём диагоналями изображаются проекции боковых ребер, идущих от вершин основания к вершине пирамиды.

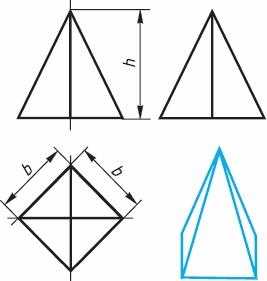
Рис. 4. Четырехугольная пирамида

Фронтальная и профильная проекции пирамиды — равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h.

Изображение тел вращения

Если круги, лежащие в основаниях цилиндра (рис. 5) и конуса 6), расположены параллельно горизонтальной плоскости проекций, их проекции на эту плоскость будут также кругами.

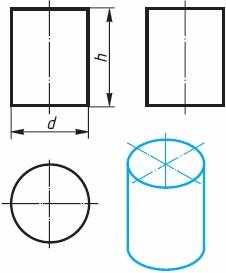
Рис. 5. Цилиндр

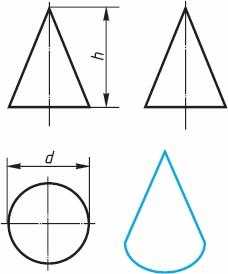
Рис. 6. Конус

Фронтальная и профильная проекции цилиндра в данном случае – прямоугольники, а конуса – равнобедренные треугольники.

На всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса.

Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря знаку диаметра Ø можно представить форму цилиндра и конуса даже по одной проекции (рис. 7, a и б). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Размеры цилиндра и конуса определяются их высотой h и диаметром основания d.

Рис. 7. Чертежи цилиндра, конуса и шара

Все проекции шара – круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии.

Благодаря знаку Ø, шар можно изображать в одной проекции (рис. 7, в). Но если по чертежу трудно отличить сферу от других поверхностей, то на чертеже добавляют слово «сфера», например: «Сфера Ø40».

Анализ геометрической формы

Вы знаете, что форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как они изображаются.

Форма каждого геометрического тела имеет свои характерные признаки. В основе формы деталей машин и механизмов также находятся геометрические тела. Чтобы понять по чертежу форму сложного предмета, его мысленно разделяют на части, представляющие собой геометрические тела, т. е. анализируют форму (рис. 8). Затем мысленно объединив эти части, воссоздают общую форму предмета.

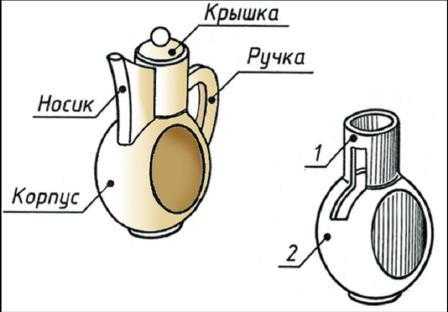
Рис. 8. Кофейник и его элементы

Геометрической формой называется внешний облик предмета, характеризующийся совокупностью его геометрических свойств. К геометрическим свойствам предметов относятся: раз­меры, пропорции, взаимное расположение составляющих элементов формы.

Предметы бывают простой и сложной формы. К предметам простой формы относятся те, которые представляют собой гео­метрические тела: цилиндр, конус, шар, призма, пирамида (рис. 9, а). К предметам сложной (составной) формы относятся такие, которые образованы сочетанием различных геометриче­ских тел (рис. 9, б).

Рис. 9. Предметы простой (а) и сложной (б) формы

Основные геометрические тела можно выявить в любой детали или предмете. Так, на рисунке 10, а в прямоугольной проекции изображена деталь, называемая валиком (от слова «вал»). В ней можно выделить такие геометрические тела, как усеченный конус 1, цилиндр 2, параллелепипед 3 и еще один цилиндр, большего диаметра – 4 (рис. 10, б).

Рис. 10. Анализ геометрической формы детали

Чтобы представить по чертежу общую форму любой детали, необходимо выявить форму всех ее элементов. Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.

Ещё проанализируем форму детали (рис. 11), состоящей из трех геометрических тел: конусов (прямого кругового и усеченного) и цилиндра.

Рис. 11. Анализ геометрической формы детали «Конус» на основе рас­членения ее на геометрические тела: 1 – конус; 2 – усеченный конус; 3 – цилиндр

 Все части, составляющие форму рассматриваемого изделия, расположены на одной оси (т. е. соосны). К основанию конуса примыкает равновеликое основание усеченного конуса. Другое основание усеченного конуса совмещается с основанием цилиндра, диаметр которого меньше диаметра конуса.

Попробуйте выполнить чертеж детали, представленной на рисунке 12.

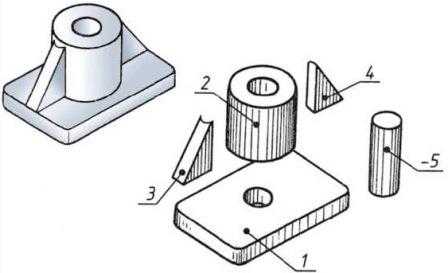
Рис. 12. Геометрическая разборка формы детали

 

 

cherch-ikt.ucoz.ru

Перспективное изображение куба | Начертательная геометрия

Перспективное изображение куба ABCDKEMG может быть построено если заданы его ортогональные проекции. Перспективное изображение куба Перспективное изображение куба ABCDKEMG 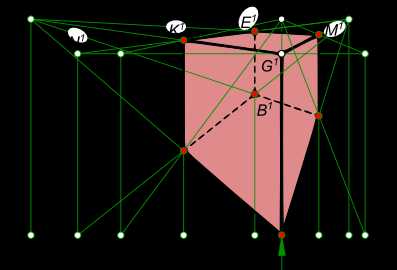Перспективное изображение куба Построение перспективного изображения куба ABCDKEMG включает в себя последовательное выполнение следующих действий: — выбор положения следа картинной плоскости. Плоскость картины совпадает с ребером DG куба; — выбор положения точки зрения S выполняем так, чтобы главный луч зрения SP, перпендикулярный картинной плоскости, проходя через нее, делил перспективное изображение куба примерно пополам; — проводим лучи из точки S в вершины куба и в пересечении их с картинной плоскостью находим точки AK, BK и CK; — параллельно A1D1 проводим вспомогательный луч из точки S и находим точку схода ребра AD; — параллельно D1C1 проводим вспомогательный луч из точки S и находим точку схода ребра DC; — точку схода ребра AD переносим с основания картинной плоскости на заданную линию горизонта в точку F1; — точку схода ребра DC переносим с основания картинной плоскости на заданную линию горизонта в точку F2; — из точки F1 проводим прямые F1D1 и F1G1; — из точки F2 проводим прямые F2D1 и F2G1; — в пересечении перпендикуляра к основанию картины в точке AK с прямыми F1D1 и F1G1 находим точки A1 и K1; — в пересечении перпендикуляра к основанию картины в точке CK с прямыми F1D1 и F1G1 находим точки C1 и M1; — из точки F1 проводим прямую F1C1 и из точки F2 проводим прямую F2K1, в пересечении данных прямых находим точку B1; — из точки F1 проводим прямую F1M1 и из точки F2 проводим прямую F2K1, в пересечении данных прямых находим точку E1; — строим перспективное изображение всех ребер куба, соединяя прямыми линиями вершины A1, B1, C1, D1, K1, E1, M1 и G1, получая замкнутый контур перспективного изображения куба. Перспективное изображение куба ABCDKEMG, когда одна из точек схода, например, F1 находится вне поля чертежа, то перспектива может быть построена и с одной точкой схода F2, если будет обеспечено последовательное выполнение следующих действий: 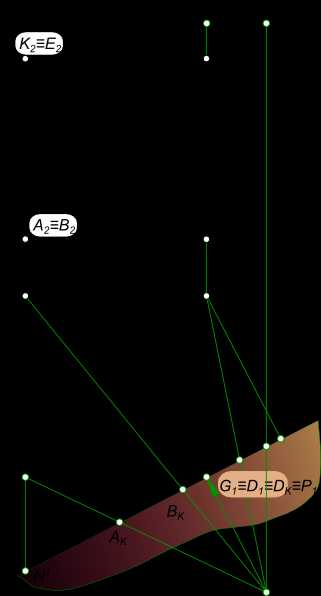Перспективное изображение куба Перспективное изображение куба — выбор положения следа картинной плоскости. Плоскость картины совпадает с ребером DG куба; — выбор положения точки зрения S выполняем так, чтобы главный луч зрения SP, перпендикулярный картинной плоскости, проходя через нее, делил перспективное изображение куба примерно пополам; — проводим лучи из точки S в вершины куба и в пересечении их с картинной плоскостью находим точки AK, BK и CK; — продолжим ребро AB до тересечения с картинной плоскостью в точке N1; — переносим точку N1 на картину, вместе с другими точками, отмеченными на следе картинной плоскости; — восстанавливаем в точке N1 перпендикуляр к основанию картины и на нем откладываем отрезок равный натуральной высоте куба; — концы данного отрезка N1 и N1 соединяем прямыми линиями с точкой схода F2; — восстанавливаем перпендикуляры к основанию картины из точек AK и BK и в пересечении их с лучами F2N1 находим ребра A1K1 и B1E1; — проводим лучи F2D1 и F2G1; — восстанавливаем перпендикуляр к основанию картины из точки CK и в пересечении его с лучами F2D1 и F2G1 находим ребро C1M1; — строим перспективное изображение всех ребер куба, соединяя прямыми линиями вершины A1, B1, C1, D1, K1, E1, M1 и G1, получая замкнутый контур перспективного изображения куба. Перспективное изображение куба ABCDKEMG так же может быть построено еще одним способом, если будет обеспечено последовательное выполнение следующих действий: 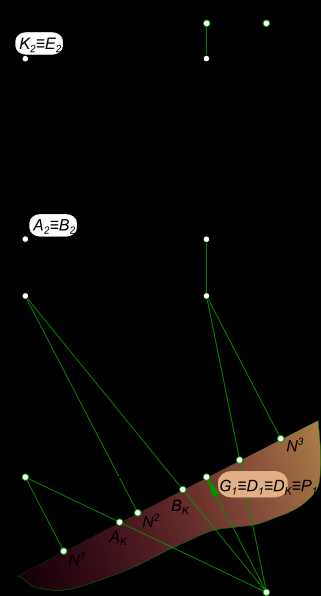Перспективное изображение куба 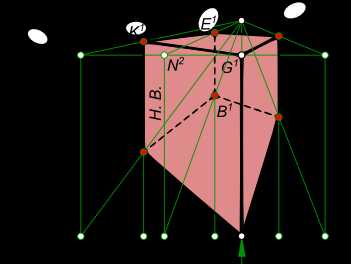Перспективное изображение куба — располагаем точку зрения так, чтобы главный луч не был направлен на дальнее ребро куба; — проводим лучи из точки S в вершины куба и в пересечении их с картинной плоскостью находим точки AK, BK и CK; — проводим прямые A1N1, B1N2 и C1N3 перпендикулярные картинной плоскости и проходящие через вершины куба; — переносим точки N1, N2 и N3 на картину, вместе с другими точками, отмеченными на следе картинной плоскости; — восстанавливаем в точках N1, N2 и N3 перпендикуляры к основанию картины и на каждом из них откладываем отрезок равный натуральной высоте куба; — концы данных отрезков N1 и N1, N2 и N2 и N3 и N3 соединяем прямыми линиями с главной точкой картины P1; — восстанавливаем перпендикуляры к основанию картины из точек AK и BK и в пересечении их с прямыми P1N1, P1N2 и P1N3 находим ребра A1K1, B1E1 и C1M1 соответственно A1K1 и B1E1; — строим перспективное изображение всех ребер куба, соединяя прямыми линиями вершины A1, B1, C1, D1, K1, E1, M1 и G1, получая замкнутый контур перспективного изображения куба. +

ngeo.fxyz.ru

Чертежи и наглядные изображения геометрических тел

Как вы уже знаете, форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела.

Куб и прямоугольный параллелепипед. Показано проецирование куба на три плоскости проекций: V, Н и W. Куб располагают так, чтобы его грани были параллельны плоскостям проекций. Тогда они изобразятся на параллельных им плоскостях проекций в натуральную величину, т. е. квадратами, а на перпендикулярных — прямыми линиями. Проекциями куба являются три равных квадрата.

Прямоугольный параллелепипед проецируется подобно кубу. Приведены три его проекции — это прямоугольники.

Изометрия параллелепипеда
На чертеже куба и параллелепипеда проставляют три размера: длину, высоту и ширину.

Приведено наглядное изображение, чертеж детали. Она слагается из двух прямоугольных параллелепипедов имеющих по две квадратные грани. Обратите знание. как проставлены на чертеже размеры. Перед размерными числами 20 и 60 нанесен знак. Он указывает на то, что эти элементы имеют форму квадрата Плоские поверхности 0™ечены тонкими пересекающиеся линиями.

Благодаря условному знаку ? оказалось возможным вычертить в одной проекции. Это ускорило выполнение чертежа.

Основания призм, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях в виде прямых линий. Боковые грани изображаются в натуральную величину на плоскостях проекций, которым они параллельны, и в виде линий па тех, которым они перпендикулярны.

Грани, наклоненные к плоскостям проекций, изображаются на них искаженными.
Размеры призм определяются высотой и размерами фигуры основания. Штрих-пунктирными линиями на чертеже проведены оси симметрии.

Построение изометрии призм начинают с основания (см. табл. 2). Затем из каждой вершины основания восставляют перпендикуляры, откладывают на них высоту и проводят линии, параллельные основанию.

Выполнение чертежей начинают также с горизонтальной проекции. Шестиугольник в основании призмы строят при помощи угольника с углами 30 и 60° так:
1. Чертят окружность, диаметр которой равен удвоенной длине стороны шестиугольника.
2. Из конечных точек вертикального диаметра проводят прямые под углом 30° к горизонтали.
3. Заканчивают построение проведением вертикальных отрезков прямых.

Вопросы для чтения чертежа:
1. Какие виды даны на чертеже?
2. На какие геометрические тела можно расчленить деталь?
3. Опишите форму детали.
4. Что означают штриховые линии на главном виде?
5. Какова высота шестиугольной призмы?
6. Чему равна длииа стороны шестиугольника?

Вслед за вопросами даны ответы на них.
Ответы на вопросы для чтения чертежа
1. Чертеж содержит главный вид и вид сверху.
2. Деталь можно расчленить на параллелепипед (основание детали), имеющий два выреза в форме параллелепипеда, и на шестиугольную призму.
3. Деталь имеет форму параллелепипеда, в центре которого установлена шестиугольная призма. Параллелепипед имеет два прямоугольных выреза.
4. Штриховыми линиями на главном виде показаны два выреза в основании детали, имеющие форму прямоугольных параллелепипедов.
5. Высота шестиугольной призмы 15 мм (25—10 15).
6. Длина стороны шестиугольника равна 15 мм (30 : 2=15).

polynsky.com.kg

ЧЕРЧЕНИЕ. Школьный интернет-учебник — Проецирование 2-4

 

Обычный рисунок изображает предмет, как он представляется глазу наблюдателя. Способ перспективного изображения используют при создании архитектурных проектов. Применение рисунка в производстве неудобно, так как он искажает форму и размеры предмета.

Чертёж, выполненный в прямоугольных (ортогональных) проекциях, является основным видом изображения, которым пользуются в технике. Он дает представление о форме и размерах предмета, но часто уступает в наглядности,  когда очень сложно представить деталь или изделие по чертежу, например рис 1а и б.  По ортогональным проекциям предмета довольно трудно представить его форму.

Рис. 1. Чертёж в прямоугольных проекциях

 В этих случаях выполняют дополнительно изображение этого предмета в аксонометрической проекции, которые значительно нагляднее (можно посмотреть здесь и здесь).

Аксонометрические проекции отличаются наглядностью. Поэтому аксонометрические проекции применяют в тех случаях, когда трудно представить деталь.

Аксонометрический чертеж (аксонометрия) – это изображение, полученное параллельным проецированием фигуры вместе с осями на некоторую плоскость так, чтобы ни одна из осей не совпадала с направлением проецирования.

   
Построение аксонометрических проекций

 В зависимости от наклона изображаемого предмета к плоскости проекций и угла, образуемого проецирующими лучами с плоскостью, получают аксонометрические проекции различного типа.

ГОСТ 2.317-69 (СТ СЭВ 1979-79) устанавливает пять видов аксонометрических проекций. Рассмотрим два наиболее употребительных вида.

Если передняя и задняя грани куба параллельны плоскости V, а проецирование осуществляется параллельными лучами, направленными под острым углом к плоскости, то получается косоугольная фронтальная диметрическая проекция.

Если расположить куб так, чтобы его грани были наклонены к плоскости V под одинаковыми углами, и проецирование производить перпендикулярными к плоскости лучами, то получится изометрическая проекция (сокращенно изометрия).

 

Положение осей

Построение аксонометрических проекций начинают с проведения аксонометрических осей.

Оси фронтальной диметрической проекции располагают, как показано на рис. 2, а: ось Х — горизонтально, ось Z – вертикально, ось Y – под углом 45° к горизонтальной линии. Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 2, б.

 Положение осей изометрической проекции показано на рис. 2, в. Оси Х  и Y располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 2, г).

Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.

 

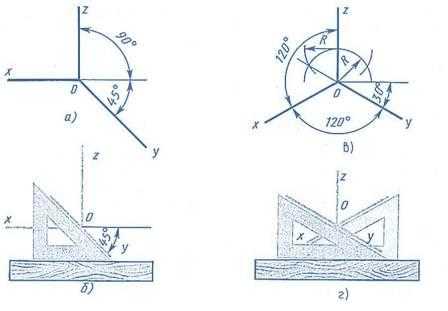
Рис. 2. Способы построения осей аксонометрических проекций

 На рис. 3, а и б показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 3, а). Наклон оси в 30° (рис. 3, б) получается при соотношении длин отрезков 3 : 5   (3 и 5 клеток).

Рис. 3. Построение аксонометрических осей на бумаге в клетку

 При построении фронтальной диметрической проекции по осям Х и Z (и параллельно им) откладывают действительные размеры; по оси У (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».

При построении изометрической проекции по осям Х, У, Z (и параллельно им) откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».

 

Построение фронтальной диметрической и изометрической проекций

 Построим фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 4.

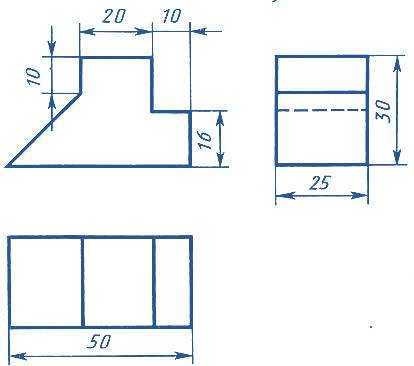
 Рис. 4. Комплексный чертеж детали

 Порядок построения проекций показан на рисунке 5:

1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты – вдоль оси Z, длины – вдоль оси Х (рис. 5, а).

2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной диметрической проекции – сокращенную в 2 раза; для изометрии – действительную (рис. 5, б).

3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 5, в).

4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 5, г).

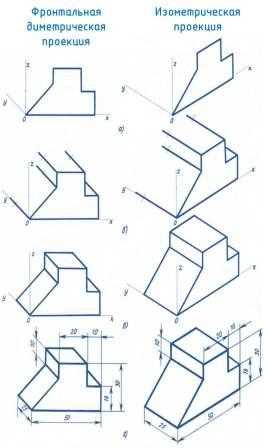
 Рис.5. Способ построения аксонометрических проекций

 Сравните левую и правую колонки на рис. 5. Что общего и в чём различие данных на них построений?

Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод, что порядок построения фронтальной диметрической и изометрической проекций, в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.

 

cherch-ikt.ucoz.ru

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

 

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника



Рис. 112. Прямоугольная и изометрические проекции круга

 

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

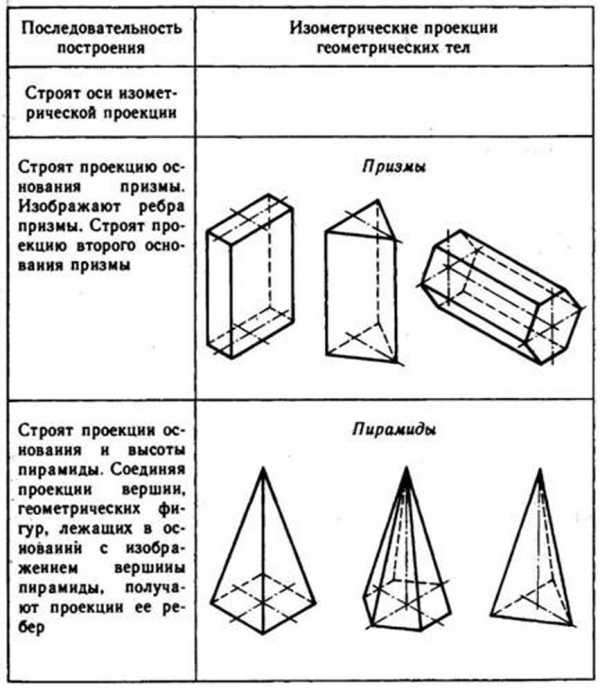
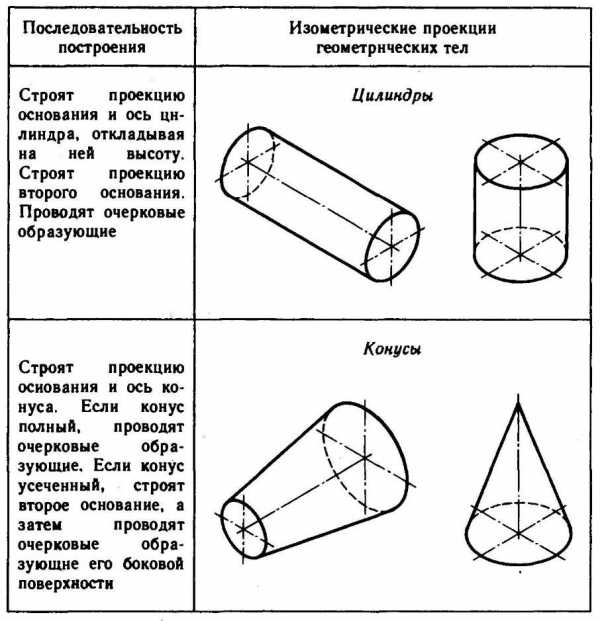
Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел





Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1)   построение осей изометрической проекции;

2)      построение изометрической проекции формообразующей грани;

3)    построение проекций остальных граней посредством изо­бражения ребер модели;

 



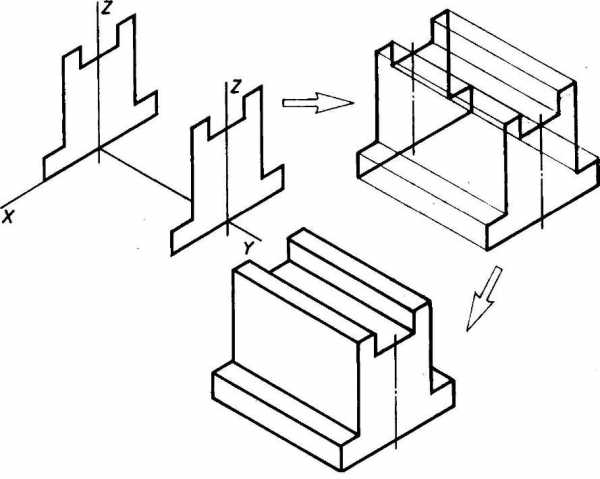
Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

 

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.



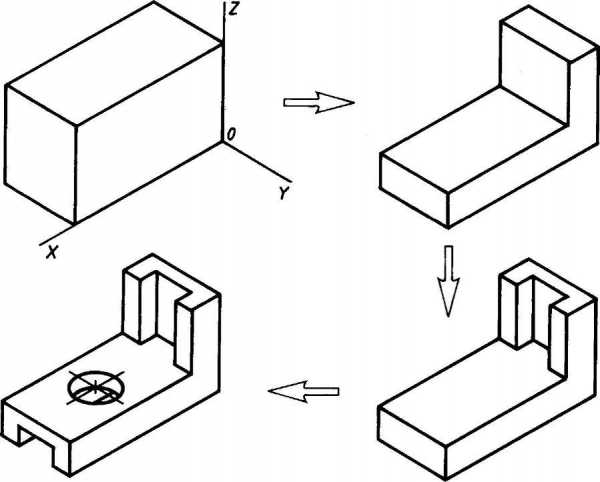
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов



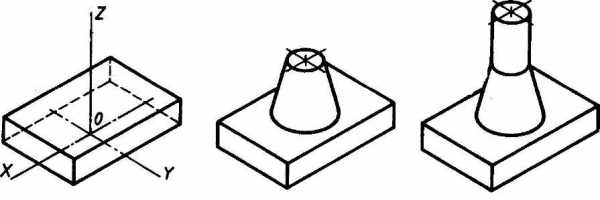
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов



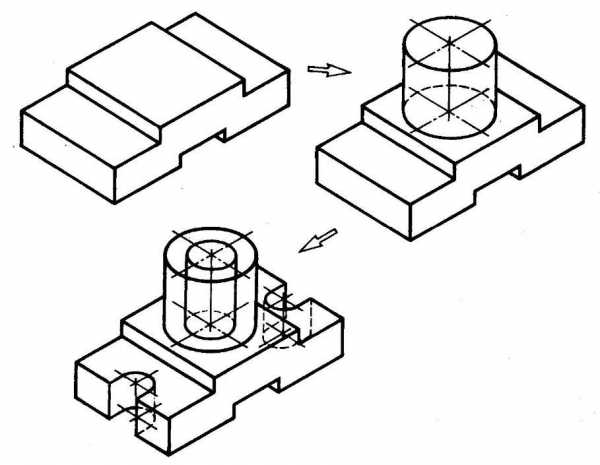
Рис. 116. Использование комбинированного способа построения изометрической проекции детали



Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

cherch.ru

Построение изометрической и диметрической проекций окружностей, расположенных в плоскостях, параллельных плоскостям проекций

Непосредственное проектирование окружности на плоскость можно заменить проектированием описанного вокруг неё квадрата с последующим вписанием в проекцию квадрата проекции окружности. При этом используются следующие свойства параллельного проектирования этих фигур: 1) точка пересечения диагоналей проекции квадрата есть центр проекции окружности; 2) точками касания проекции окружности к проекции квадрата остаются средние точки сторон проекции квадрата; 3) на­правление сторон проекции квадрата является направлением двух сопряжённых диаметров проекции окружности.

Построим изометрическую проекцию окружности, лежащей в какой- нибудь координатной плоскости. Для этого возьмём куб, в грани которого впишем окружности. Куб расположим так, чтобы его грани были параллельны координатным плоскостям (фиг. 189).

Проекция куба имеет форму правильного шестиугольника, а проекцией каждой его грани является ромб.

Равенство ромбов—проекций квадратов—предопределяет и равенство эллипсов—проекций, вписанных в грани куба окружностей. Направления главных осей эллипса в изометрических проекциях совпадают с диагоналями ромба, в который вписан эллипс.

Следует запомнить простое правило нахождения большой и малой осей: малая ось всегда параллельна той оси, которой нет в названии плоскости эллипса. Так, например, если для эллипса плоскости OXZ нет названия оси OY, то малая ось этого эллипса параллельна оси OY. Большая ось всегда перпендикулярна к малой.

Можно это же условие выразить иначе: малая ось эллипса совпадает по направлению либо параллельна перпендикуляру к плоскости, в которой лежит спроектированная в эллипс окружность.

Чтобы построить эллипс по главным его осям, кроме направления, необходимы и размеры этих осей.

Как известно, независимо от положения плоскости проекций, большая ось эллипса всегда равна величине диаметра окружности, а малая в изометрической проекции равна 0,58 диаметра окружности. Прибли­жённо можно принять отношение между осями эллипса, равным 3:5.

Если построение окружности выполняется в масштабе 1,22:1, то при построении большой оси надо взять 1,22 d, а для малой ³/₅ этой вели­чины, т. е. 0,725 d.



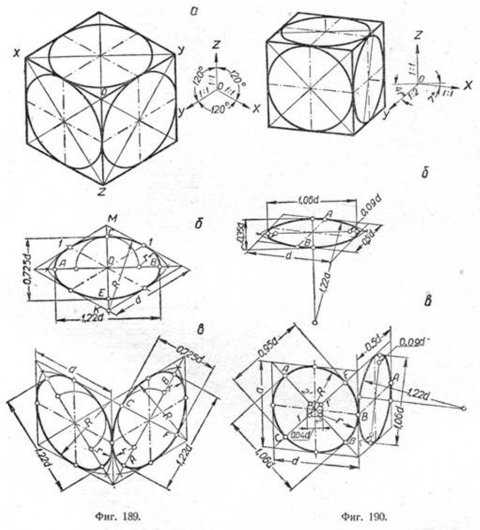
В практике часто вместо построения эллипсов лекальные кривые за­меняют циркульными и строят овал с тем же отношением 3:5 между главными осями.

На фиг. 189,б и в приведён способ построения овалов, заменяющих вписанные эллипсы. На одном чертеже овал вписан в ромб, соответ­ствующий горизонтальной грани куба, а на втором—двум боковым граням.

На фиг. 190 дана диметрическая прямоугольная проекция окруж­ности. Свойства, перечисленные в предыдущем случае, остаются в силе и здесь.

Эллипс, в который проектируется окружность, лежащая на передней грани куба, имеет, как и в случае изометрических проекций, главные оси, сливающиеся с диагоналями куба. Конечные точки осей могут быть определены как точки, делящие каждую из полудиагоналей ромба на части в отношении 7:10.

Для боковой грани и для грани верхнего основания куба направление малой оси эллипса параллельно аксонометриче­ской оси OY. Зная направление малых осей эллипсов, легко определить направление больших осей.

Для боковой грани боль­шая ось наклонена к оси OZ на угол 7°, а для грани верх­него основания большая ось будет горизонтальной прямой.

При проектировании в масштабе 1,06:1 длина боль­шой оси эллипса равна 1,06 d, где d  — диаметр окружности.

Что касается малой оси, то для фронтальной грани она равна 0,89, т. е. около 0,9 большой оси. Для граней бо­ковой и горизонтальной малая ось принимается равной 0,35 ребра куба или 1/3 большой оси эллипса.

Практически в этом слу­чае вместо эллипсов можно строить овалы.

На фиг. 190, б и в пока­заны способы построения ова­лов для каждой грани от­дельно.

И, наконец, при косо­угольном проектировании диметрическая проекция фрон­тальной грани куба проекти­руется без искажений; очевидно, и окружность, вписанная в эту грань, проектируется в окружность (фиг. 191, а и в).

Боковая грань и грань верхнего основания куба по­чти не отличаются по форме от соответствующих граней, построенных в прямоугольной проекции.

Овалы в этом случае вычерчиваются почти так же, как и на соот­ветственных гранях куба предыдущего случая.

www.nacherchy.ru