Как с помощью циркуля нарисовать звезду: Вопрос: Как нарисовать звезду? — Хобби и рукоделие
08.04.1973 


 Разное
Разное
Вопрос: Как нарисовать звезду? — Хобби и рукоделие
Содержание статьи:
Как нарисовать пятиконечную звезду. Уроки рисования для начинающих и детей.
Показать описаниеЗдравствуйте! Предлагаю вашему вниманию видеоролик, где я показываю, как очень просто нарисовать пятиконечную звезду..
.
Если вам интересно посмотреть на мои работы, загляните на мою страницу вhttps://plus.google.com/u/0/b/103343321244377959725/103343321244377959725/posts?pageId=103343321244377959725. Мои уроки подходят для новичков и абсолютных чайников. Если вы желаете научиться рисовать, лепить, вообще “творить” имея только одно лишь желание, никакого опыта, если мой „уровень“ вас устаивает, Вступайте в мой творческий кружок,подписывайтесь на канал, где я регулярно, буду выкладывать новые видео по рисованию, лепке или изготовлению различных поделок..
Рисуем, вырезаем снежинки, материм поделки на новый год, на рождествоhv=HTGen6LLNU8&list=PLZe8Hu6lxXMzQXlj3OIO6YMQERJ_n3gVi.
рисуем знаки зодиакаhttps://www.youtube.com/watch?v=Ry93pDrm-nE&list=PLZe8Hu6lxXMx-DKJeWsJokGawrke8G5Ca.
Рисуем животных-игрушекhttps://www.youtube.com/watch?v=0-eKdoE5U1I&list=PLZe8Hu6lxXMy8izfMSftx8nRUFN3FwKue
Видео взято с канала: Творческий Кружок с Ниной Ной
Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуля
Видео взято с канала: Lostas
Как начертить пятиконечную звезду, how to draw five pointed star
Видео взято с канала: Pavel Kubarkov
Как нарисовать ЗВЕЗДУ / ЗВЁЗДОЧКА раскраска мультик для детей / Ай Мульт
Показать описаниеРаскраска для детей ЗВЕЗДА. Мультик Раскраска. Учим цвета. Учимся, как рисовать раскраску-мультик ДЛЯ МАЛЫШЕЙ. Учим цвета. А также вместе с тем, как мы рисуем ЗВЁЗДОЧКУ, мы учим цвета на русском языке. Кроме этой раскраски для детей, на нашем канале есть и другие раскраски для детей, такие как: Раскраска для детей ракета, мороженое, радуга, фрукты, животные, машинки, кораблики, самолёты, цифры, растения, вещи и многое другое.
Видео взято с канала: Lagard
Как просто нарисовать Звезду поэтапно, шаг за шагом. Учимся рисовать ровную, красивую звезду. #539
Видео взято с канала: Рисуем простые рисунки
Как нарисовать звезду?!!
Видео взято с канала: Ульяна КэтЛайф
Как нарисовать правильную пятиконечную звезду
Видео взято с канала: Просто Сделать
Как нарисовать пятиконечную звезду циркулем
Мы слышали это нарисовать пятиконечную звезду все сложно. Это как раз наоборот, и мы покажем вам это простыми шагами. Вы будете удивлены. Есть два способа нарисовать звезду: с помощью циркуля, линейки и транспортира или от руки. Линейка и циркуль помогут рисовать идеальная пятиконечная звезда, или любую другую звезду, которую вы хотите сделать.
Изучив метод, описанный здесь, вы можете рисовать столько точек, сколько захотите, 3, 5 или 12. Вам не обязательно любить математику или геометрию, но небольшие знания действительно помогут вам в этом. Каждый великий живописец или художник в истории знал основные геометрические принципы, позволяющие рисовать, раскрашивать и лепить впечатляющие произведения искусства. Спросите да Винчи или Микеланджело.
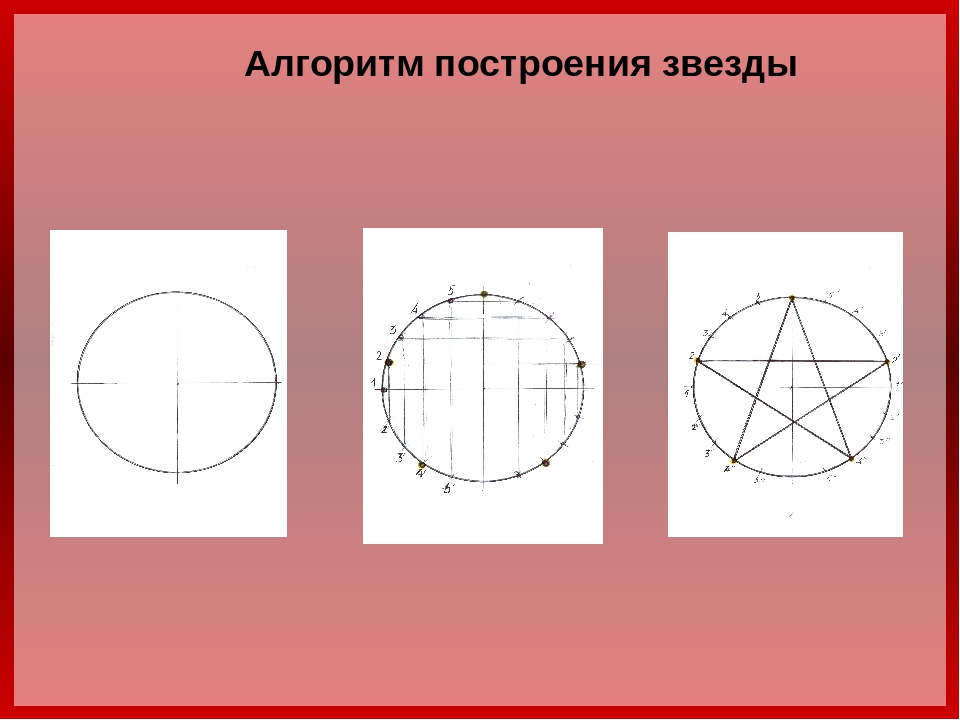
Лучше всего начать с круга. Главное — знать, что у круга 360 градусов. Вы можете нарисуйте звезду внутри круга. Это означает, что если вы хотите нарисовать пятиконечную звезду, вы просто разделите круг на 5 частей.
Формула 360 градусов: 5 наконечников = 72 градуса
Вы делите круг на углы 72 градуса и получаете 5 баллов на Обведите круг на одинаковом расстоянии друг от друга. Чтобы нарисовать звезду, вам понадобятся линейка, циркуль и транспортир. Отныне все работы по рисованию будут выполняться этими инструментами.
Действия, которые необходимо выполнить:
Нарисуйте простой крест.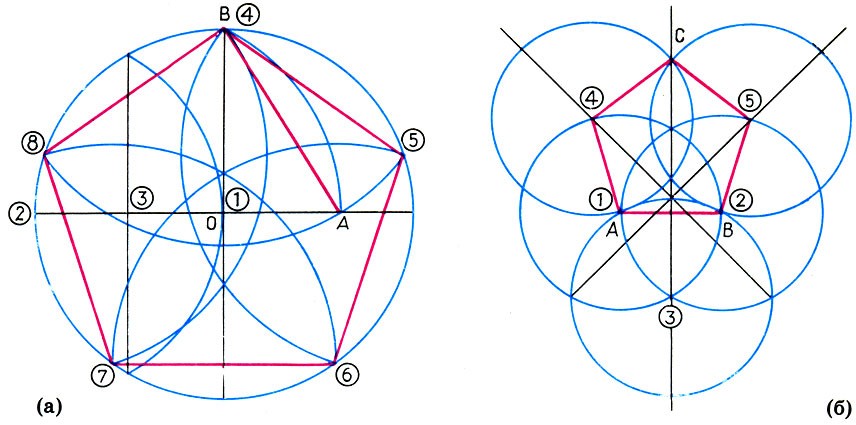 Проведите только линии, не делая больших разметок карандашом.
Проведите только линии, не делая больших разметок карандашом.
Определитесь с диаметром и нарисуйте круг с помощью циркуля.
Используя транспортир, отметьте угол 72 градуса. Точка пересечения пунктирной линии круга является одной из 5 точек звезды.
Расстояние между точкой наверху круга и точкой, которую вы только что отметили, — это расстояние между каждой из точек звезды. Это именно то, что вам нужно сделать.
С помощью циркуля определите расстояние между этими двумя начальными точками и разделите круг, как показано на изображении.
Вы получите 5 очков (1, 2, 3, 4, 5) с точным расстоянием друг от друга. Другими словами, расстояние между каждой точкой составляет 1/5 длины окружности.
Соедините один конец с другими, как вы видите на изображении, и вы идеальная пятиконечная звезда будет готова.
Если вы хотите прочитать больше статей, похожих на Как нарисовать пятиконечную звезду циркулем, рекомендуем вам войти в нашу категорию «Поделки и свободное время».
Как чертить правильный пятиугольник. Правильный пятиугольник: необходимый минимум информации
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.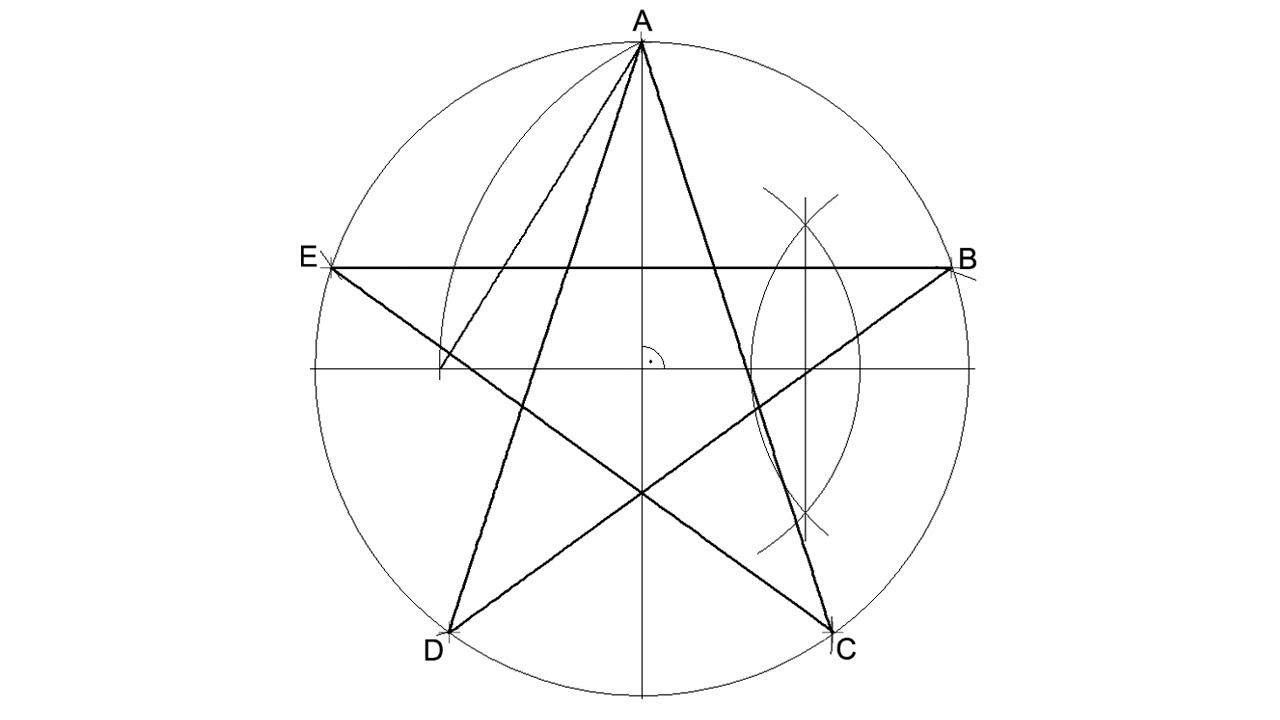
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.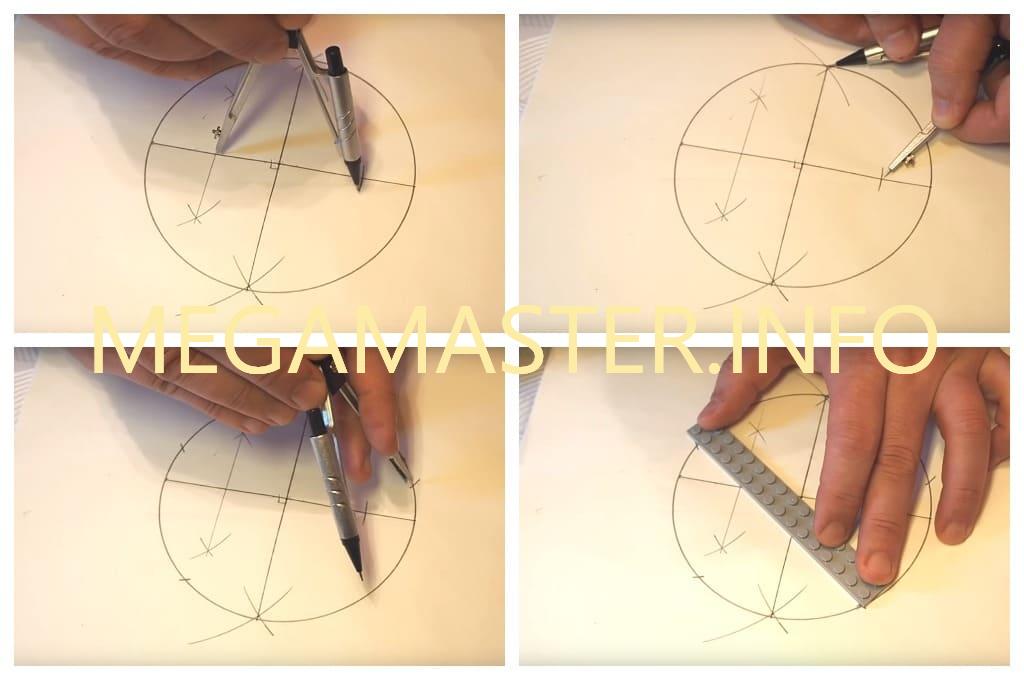
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.
Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку.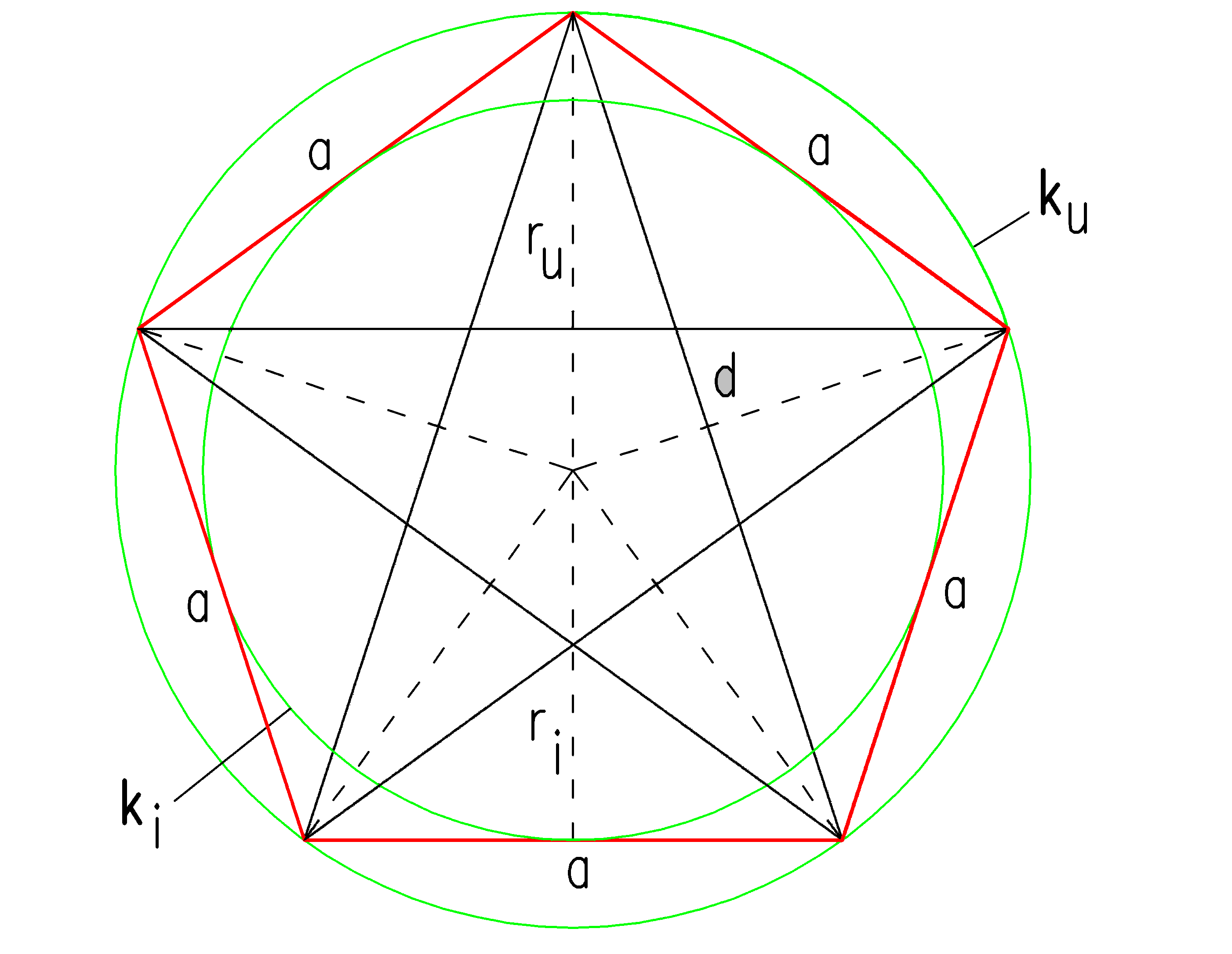 Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.
Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD.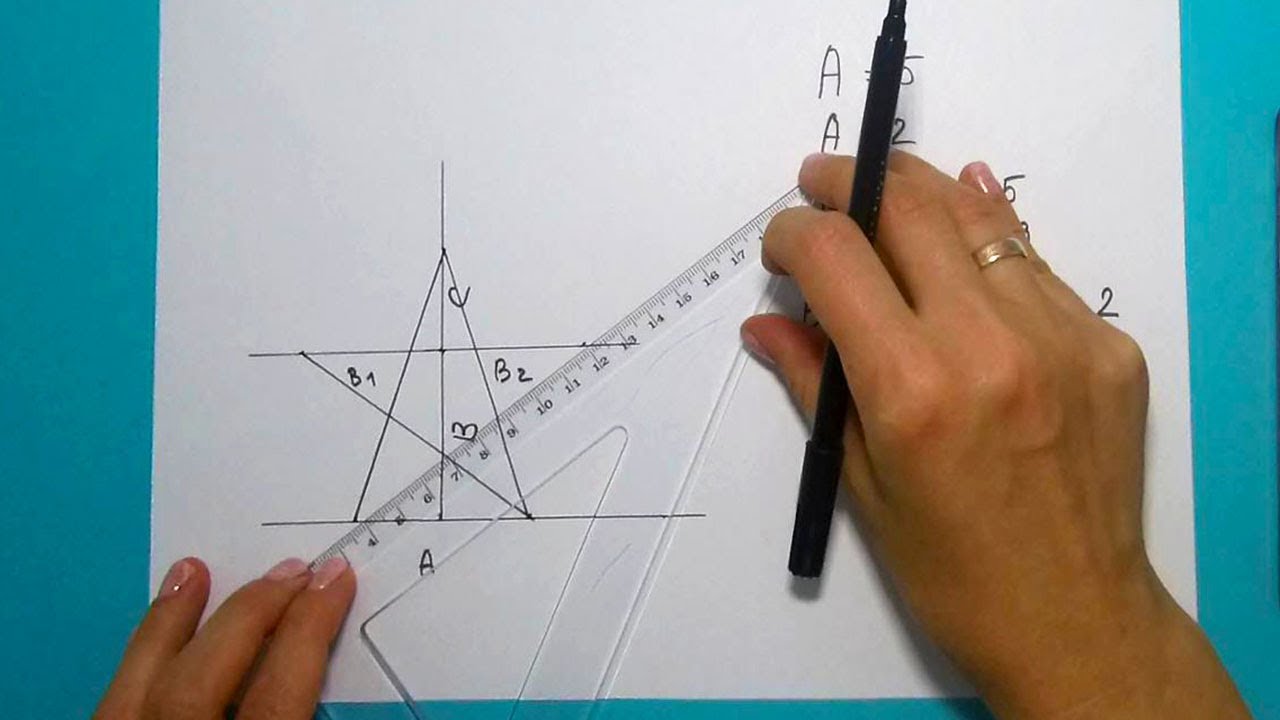 Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.
(на рисунке — завершенная, но незаполненная пентаграмма)
Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)
Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.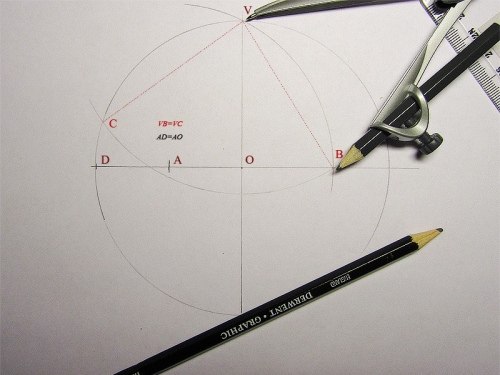 5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
5.3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).
5).
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
из центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 — a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN 2 = а 2 – (а/2j) 2 = а 2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.
В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci — сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.
им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
«Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения»
| Месяцы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Пары кроликов | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u 1 , u 2 … u n
в которой каждый член равен сумме двух предыдущих, т.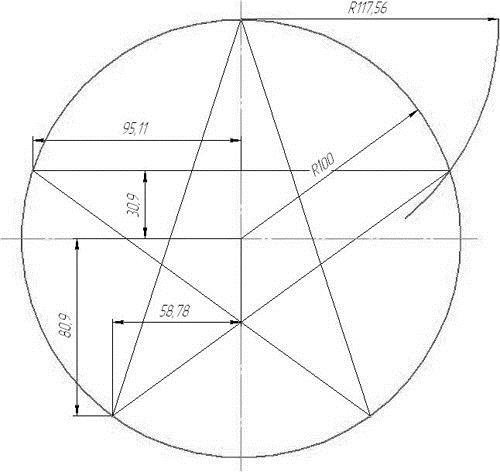 е. при всяком n>2
е. при всяком n>2
u n =u n -1 +u n -2 .
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2. 0000, что больше фи на 0.3820
0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1: 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения.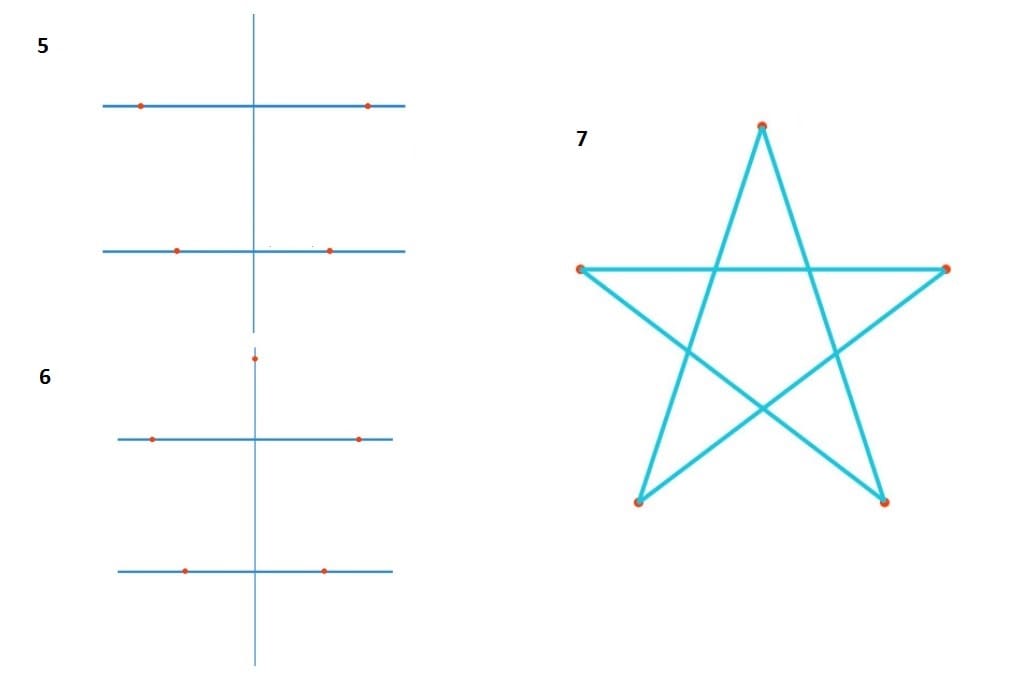 В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16…(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов.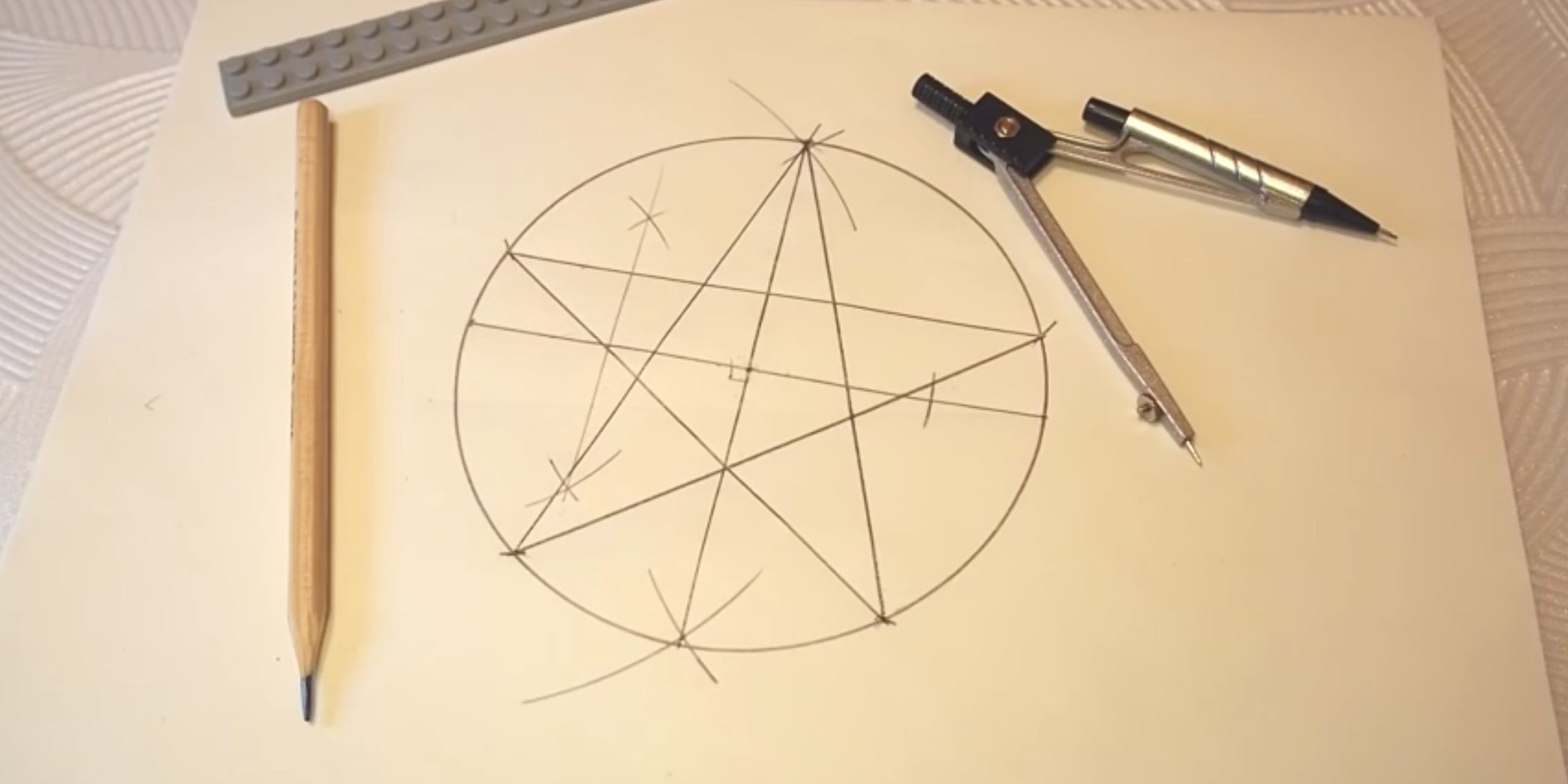 Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x S+1 – x S – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие.
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке, делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»
Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»
Список литературы
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал «Наука и техника»
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964
8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998
9. Информация из интернета.
Матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку…
Не повлияют на этот результат. Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…
Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…
Уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9). Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции. Ритмы сердца и мозга. Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает…
Толковый словарь Ожегова гласит, что пятиугольник представляет собой ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Чем интересен правильный пятиугольник?
Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!
Основные свойства и формулы
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
- Центральный угол α = 360 / n = 360/5 =72°.
- Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
- Отношение диагонали к боковой стороне равно (1+√5) /2, то есть (примерно 1,618).

- Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:
- если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
- в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
- бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.
- Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
- если имеется вписанная или описанная окружность, то используется одна из двух формул:
S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;
- площадь можно также определить, зная лишь длину боковой стороны а:
S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .
Правильный пятиугольник: построение
Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.
Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.
1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.
2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.
3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.
4. На середине расстояния между точками О и В постройте точку С.
5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.
6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить
8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!
Поделитесь статьей с друзьями:
Похожие статьи
Как рисовать звезду
Казалось бы, так легко изобразить звезду, но на самом деле очень тяжело ровно и правильным очертанием нарисовать ее. Перед тем, как начать рисовать звезду, нужно выполнить пятиконечную звезду (при помощи циркуля), и изобразить на простой бумаге окружность. Далее разделить ее на ровные частицы. Для этого соблюдайте несколько правил, которые связаны с геометрией.
Далее разделить ее на ровные частицы. Для этого соблюдайте несколько правил, которые связаны с геометрией.
Берем стандартную пятиконечную звезду (звездочка шерифа). Для рисунка можно также использовать морской вариант звезды или куранты, разукрасив цветным карандашом красного оттенка или краской.
Начальный этап изображения звезды
В первую очередь нарисуйте ровную окружность при помощи циркуля или просто обведите чашку или стакан, положив его краюшками на бумагу. Выполняйте очень легкий нажим карандашом, чтобы потом было проще убрать данный контур, используя ластик. Окружность следует выполнять такой же размерности, какой вы собираетесь изображать звезду.
Теперь требуется разделить окружность на пять равных частиц. Для этого мы используем основное правило науки «геометрия». Сначала измеряем с помощью линейки диаметр окружности. После этого умножаем 6,28 на полученный диаметр. То значение, которое у вас образуется, и будет выступать как расстояние между вершинами пятиконечной звездочки. Располагаем данные точки на равномерном расстоянии друг от друга. Теперь соединяем точки.
Располагаем данные точки на равномерном расстоянии друг от друга. Теперь соединяем точки.
Последние штрихи изображения звезды
Для придания объемности изображению, следует выполнить ей верхней грани, одна из областей которых будет затененной. Грани выполнять очень легко, то есть, соединяем верхние точки острых уголков с нижними тупыми уголками и звездочка готова к разукрашиванию или штрихованию обычным карандашом.
Если вы, верно, выполнили разметку верхних точек, то звездочка должна быть с равномерными сторонами и промежутками между вершинами. Самым обычным методом проверки считается поворот листка с бумажкой, где изображена звезда и смотрите, как она будет смотреться со всех сторон. При желании, можно корректировать изображение. Прежде чем выполнить окончательное раскрашивание или штрихование карандашом.
Если вы изобразили морскую звездочку, то четкие грани можно и не делать. Затемняем поочередно каждую сторону, как и в примере с пятиконечной звездой, только уже более легкими штрихами.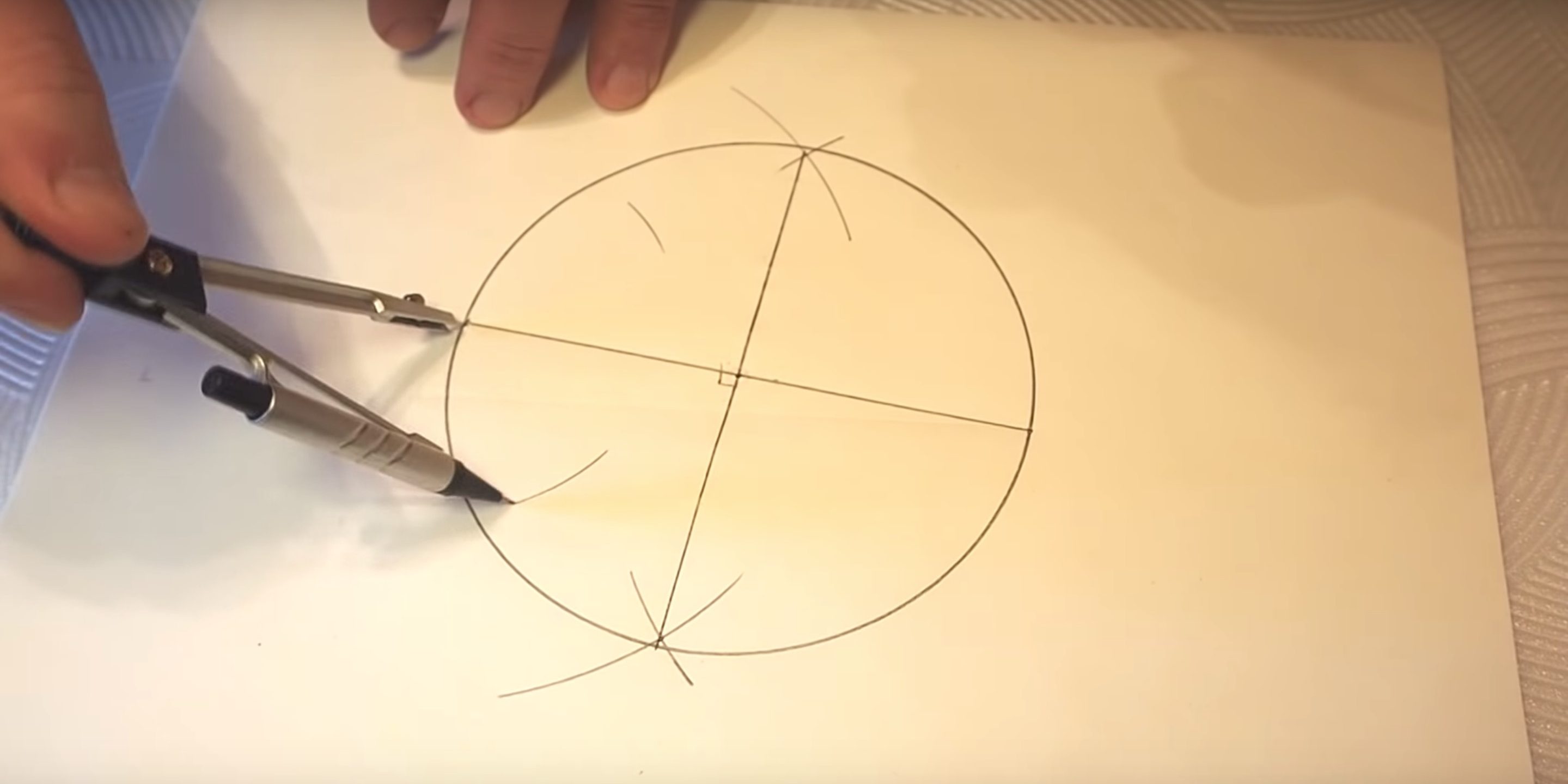 Для звездочки шерифа необходимо в обязательном порядке заняться штриховкой всей части одной из сторон для придания звезде больше объемности и контрастности.
Для звездочки шерифа необходимо в обязательном порядке заняться штриховкой всей части одной из сторон для придания звезде больше объемности и контрастности.
Как нарисовать многоконечную звезду — презентация онлайн
1. Городская конференция младших школьников «Открытие» Секция математика Как нарисовать многоконечную звезду
Автор:Квич Александр ученик 6 Б класса
МАОУ «СОШ № 8»
Руководитель:
Чернова Ольга Васильевна
учитель математики
МАОУ «СОШ № 8»
Проблема исследованиякак нарисовать многоконечную звезду.
Объект исследования –
многоконечная звезда.
Предмет исследования – рисование
многоконечных звезд.
Цель исследования – получить способы
рисования многоконечных звезд.
Задачи:
1.Изучить историю многоконечных звезд.

2.Проанализировать пути их построения и
найти некоторые закономерности.
3.Исследовать звездчатые многоугольники.
4.Рассмотреть возможные пути построения
правильной пятиконечной звезды.
5.Изготовить пятиконечную звезду из
полоски бумаги.
Гипотеза. Если использовать окружность
как инструмент для рисования, то можно
нарисовать многоконечную звезду:
• 1. Не отрывая карандаша от листа бумаги.
• 2.Определить: сколько видов
многоконечных звезд можно построить,
отрывая карандаш от листа бумаги и
вывести формулу.
• 3.Построить правильную многоконечную
звезду.
Методы исследования: сбор, изучение,
анализ, обобщение теоретического и
практического материала, построение
многоконечных звезд различными
способами, изготовление звезд .
5. 1.Из истории звезд Пятиконечные звезды
6. Почему у Пентагона пять углов
7. Шестиконечные звезды
9. Звезда Давида
10. Восьмиконечные звезды
11.
 Восьмиконечные звезды
Восьмиконечные звезды12. ХРИСТИАНСКАЯ ДЕВЯТИКОНЕЧНАЯ ЗВЕЗДА
Она образовалась приблизительно V-VI век от РХ
Дары Святого Духа: 1 Коринфянам 12 :
1 Слово мудрости
2 Слово знания
3 Вера
4 дар исцелений
5 чудотворение
6 пророчество
7 различение духов
8 разные языки
9 истолкование языков
Плоды Святого Духа: Гагатам 5 :
1 Любовь
2 Радость
3 Мир
4 Долготерпение
5 Благость
6 Милосердие
7 Вера
8 Кротость
9 Воздержание
13. Девятиконечные звезды
Удивительный город Пальманова . Италия.15. 2.Рисование звезд, не отрывая карандаша от листа бумаги
16. Рисование восьмиконечной звезды
17. 3. Исследование многоконечных звезд. Виды звезд.
5-конечные6- конечные
7- конечные
8- конечные
9 -конечные
18. Виды звезд
10- конечные11- конечные
12- конечные
Количество вершин
правильного многоугольника
Количество многоконечных
звезд
5
1
6
1
7
2
8
2
9
3
10
3
11
4
12
4
Вывод: 1.
 Число вершин многоугольника n- нечетное число, то
Число вершин многоугольника n- нечетное число, торазличных многоконечных звезд будет (n-3) : 2 вида.
2.Число вершин многоугольника n — четное число, то
различных многоконечных звезд будет (n-4) : 2 вида.
4. Построение правильной пятиконечной
звезды
А1
С
А1
С
А1
в
А1
в
А5
А4
А2
А3
Построение пятиугольника по заданной
его стороне
23. Деление окружности на пять равных частей
МО
К
24. Изготовление пятиконечной звезды из полоски бумаги
25. ВЫВОДЫ
1.Изучена история многоконечных звезд.2.Проанализированы пути их рисования и
найдены закономерности.
3.Исследованы звездчатые многоугольники,
выведена формула для определения
количества видов звезд для n- угольника.
4. Изучены и рассмотрены способы построения
правильной пятиконечной звезды.
6. Получены способы рисования правильных
многоконечных звезд.
5.Изготовлена пятиконечная звезда из полоски
бумаги.
6.Доказана гипотеза.
26. Спасибо за внимание!
Как рисовать маленькую звездочку
Раньше мы уже рисовали пятиконечную звезду. Сегодня снова предлагаем изобразить звезду. Но на этот раз она будет маленькая и веселая, с милой улыбкой. Привлеките к рисованию ребенка. Уверяем, ему это понравиться.
1
Круг
На листе бумаги с помощью циркуля рисуем большой круг.
2
Делим круг
Разделяем круг на ровные части с помощью горизонтальной и вертикальной линий.
3
Пятиугольник
Теперь рисуем пятиугольник внутри фигуры.
4
Треугольник
Внутри пятиугольника поместите треугольник.
5
Углы звезды
Проводим линии от верхних парных углов пятиугольника к нижним.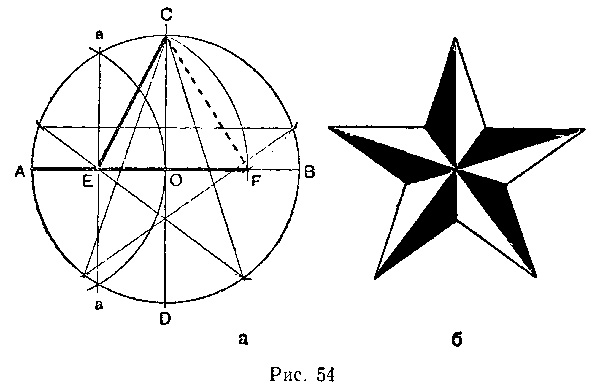
Далее проводим линию, соединяя противоположные углы.
6
Убираем ненужные линии
Стираем круг и пятиугольник.
Теперь стираем ненужные линии внутри звезды.
7
Контур
Обведите звезду ровными линиями на маленьком расстоянии. Так мы придадим звездочке красивый контур.
8
Лицо
Рисуем лицо звезды. Начинаем с глаз, они овальные. Также заметьте, что звездочка смотрит вниз.
Рисуем носик, улыбочку и язык.
9
Раскрашиваем
Раскрасьте звезду разными оттенками желтого цвета. Глаза голубые, а язычок красный.
10
Коллаж
Видео к материалу
Если вы увидели ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Понравилась инструкция?
5 Да Нет 2Еще инструкции на эту тему:
Построение правильного пятиугольника с помощью циркуля. Как нарисовать звезду с помощью линейки быстро? Получение с помощью полоски бумаги
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко.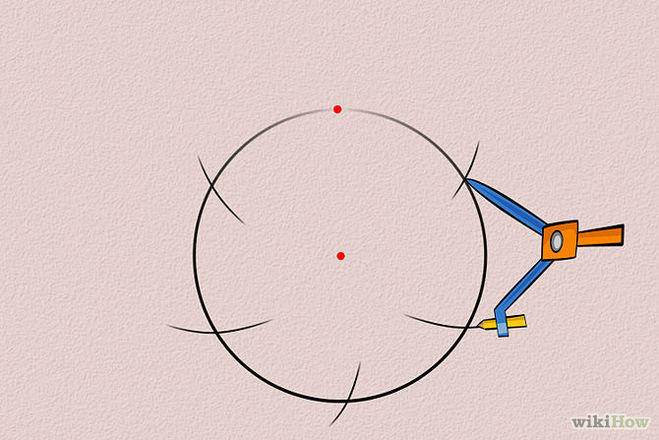 Все вспомогательные линии убираются.
Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.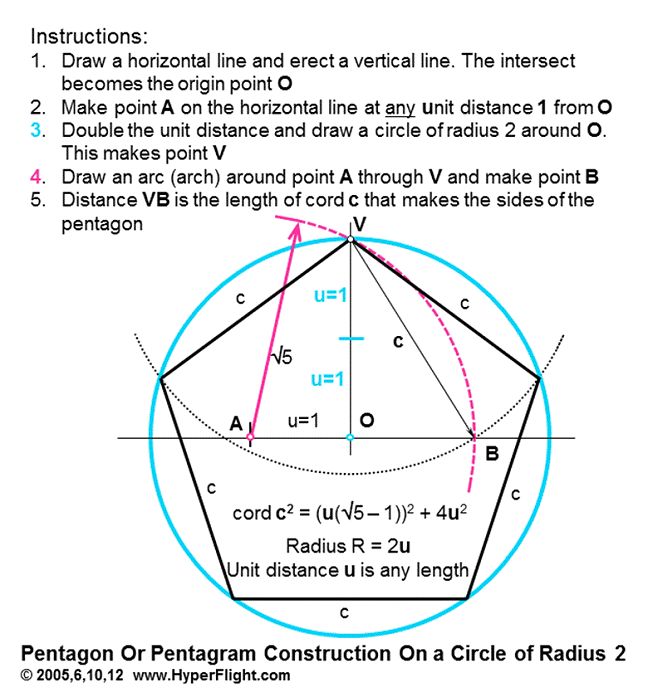
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
5. 3. Золотой пятиугольник; построение Евклида.
3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольникаиз центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 — a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN 2 = а 2 – (а/2j) 2 = а 2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.
В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci — сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.
им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
«Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения»
| Месяцы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Пары кроликов | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u 1 , u 2 … u n
в которой каждый член равен сумме двух предыдущих, т. е. при всяком n>2
е. при всяком n>2
u n =u n -1 +u n -2 .
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2. 0000, что больше фи на 0.3820
0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1: 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16…(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов.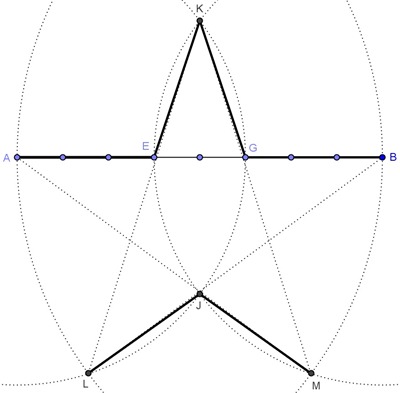 Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x S+1 – x S – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие.
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке, делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: «Геометрия обладает двумя великими сокровищами.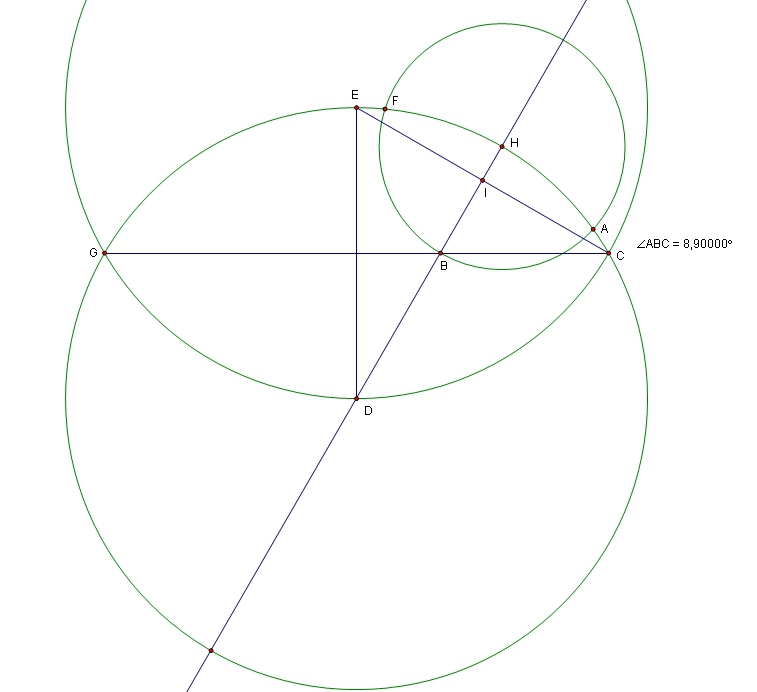 Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»
Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»
Список литературы
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал «Наука и техника»
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964
8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998
9. Информация из интернета.
Матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку…
Не повлияют на этот результат.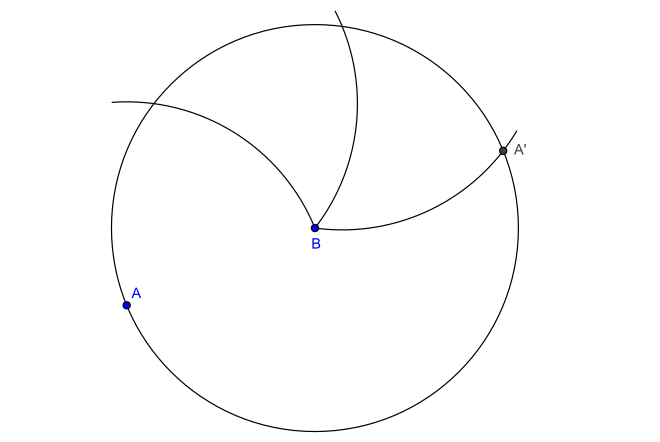 Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…
Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…
Уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9). Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции. Ритмы сердца и мозга. Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает…
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.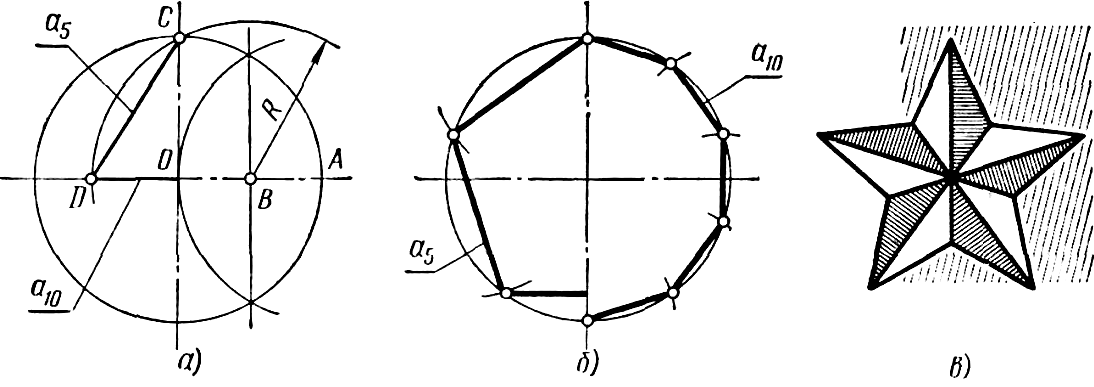
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…
е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…
Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…
Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…
Инструкция
Постройте еще один диаметр, перпендикулярный диаметру МН. Для этого циркулем проведите дуги из точек М и Н с одинаковым радиусом. Радиус выбирайте такой, чтобы обе дуги пересеклись между собой и с данной окружностью в одной точке. Это будет первая точка А второго диметра. Проведите через нее и точку О прямую. Получится диаметр АВ, перпендикулярный прямой МН.
Для этого циркулем проведите дуги из точек М и Н с одинаковым радиусом. Радиус выбирайте такой, чтобы обе дуги пересеклись между собой и с данной окружностью в одной точке. Это будет первая точка А второго диметра. Проведите через нее и точку О прямую. Получится диаметр АВ, перпендикулярный прямой МН.
Найдите середину радиуса ВО. Для этого циркулем с радиусом окружности проведите дугу из точки В так, чтобы она пересекла окружность в двух точках С и Р. Через эти точки проведите прямую. Данная прямая поделит радиус ВО ровно пополам. Поставьте точку К в месте пересечения СР и ВО.
Соедините точки М и К отрезком. Задайте на циркуле расстояние равное отрезку МК. Из точки М проведите дугу так, чтобы она пересекала радиус АО. В месте данного пересечения поставьте точку Е. Полученное расстояние МЕ соответствует длине одной стороны вписываемого пятиугольника.
Постройте оставшиеся вершины пятиугольника. Для этого установите расстояние ножек циркуля равным отрезку МЕ.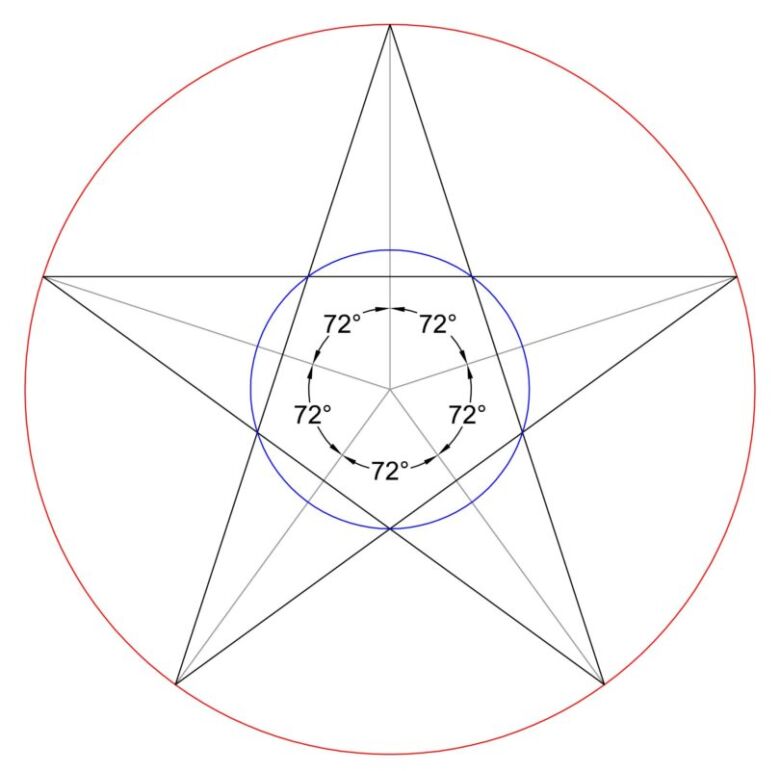 Из первой вершины пентагона М проведите дугу до пересечения с окружностью. Точка пересечения и будет второй вершиной F. Из полученной точки в свою очередь также проведите дугу того же радиуса с пересечением окружности. Получите третью вершину пентагона G. Аналогичным образом постройте остальные точки S и L.
Из первой вершины пентагона М проведите дугу до пересечения с окружностью. Точка пересечения и будет второй вершиной F. Из полученной точки в свою очередь также проведите дугу того же радиуса с пересечением окружности. Получите третью вершину пентагона G. Аналогичным образом постройте остальные точки S и L.
Соедините полученные вершины прямыми отрезками. Вписанный в окружность, правильный пятиугольник MFGSL построен.
Источники:
- Правильные многоугольники
Шестиугольник — это многоугольник, который обладает шестью углами. Для того, чтобы начертить произвольный шестиугольник, нужно проделать всего 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с другом по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание
Особым типом шестиугольника является правильный шестиугольник. Он называется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника можно описать или вписать окружность. Стоит отметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны правильного шестиугольника делятся пополам.
Он называется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника можно описать или вписать окружность. Стоит отметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны правильного шестиугольника делятся пополам.
Полезный совет
В природе правильные шестиугольники обладают большой популярностью. К примеру, каждая пчелиная сота обладает правильной шестиугольной формой.
Или кристаллическая решетка графена (модификация углерода) тоже обладает формой правильного шестиугольника.
Изображения геометрических фигур используются для создания многих и многих игр, коллажей, иллюстраций. Используя средства фотошоп, можно нарисовать любую объемную фигуру, в том числе, и шестигранник.
Вам понадобится
Инструкция
Откройте новый документ. На инструментов выбирайте Polygon Tool. На панели свойств установите sides=6 и color любой, на ваш вкус. Зажав клавишу Shift, нарисуйте . Наведите курсор на фигуру, нажмите на правую клавишу мыши и выбирайте команду Rasterize Layer.
Наведите курсор на фигуру, нажмите на правую клавишу мыши и выбирайте команду Rasterize Layer.
Дважды скопируйте этот слой (Ctrl+J), чтобы у вас получилось три шестиугольника. Встаньте на новый слой. Зажав Ctrl, щелкните по иконке с изображением новой , чтобы получить выделение. На панели инструментов установите цветом переднего более темный оттенок. При помощи инструмента Paint Bucket Tool залейте шестиугольник. Опять перейдите на новый слой и залейте фигуру подходящим . Таким образом, ваши шестиугольники будут окрашены в разные оттенки одного цвета.
При помощи инструмента Move Tool расположите шестиугольники так, как показано на рисунке. При этом учитывайте, где в вашей картине будет расположен источник света. Там, куда падает свет, должна находиться более светлая грань. Самая темная грань будет в тени.
Для слоев с шестиугольниками, которые изображают боковые грани, установите Opacity=50%. На панели инструментов выбирайте Eraser Tool. Установите hardness=100% и начинайте осторожно и аккуратно стирать лишнее изображение. Для того, чтобы удалить ненужный цвет возле грани, поступайте следующим образом: уменьшите диаметр резинки, чтобы не захватить лишнего. Наведите курсор на один конец ребра шестигранник а и щелкните левой клавишей мыши. Затем переведите курсор на другой конец, нажмите клавишу Shift и опять щелкните левой клавишей. Получится ровная пустая полоска. Повторите эту процедуру столько раз, сколько потребуется, чтобы убрать ненужный фон вокруг фигуры.
Для того, чтобы удалить ненужный цвет возле грани, поступайте следующим образом: уменьшите диаметр резинки, чтобы не захватить лишнего. Наведите курсор на один конец ребра шестигранник а и щелкните левой клавишей мыши. Затем переведите курсор на другой конец, нажмите клавишу Shift и опять щелкните левой клавишей. Получится ровная пустая полоска. Повторите эту процедуру столько раз, сколько потребуется, чтобы убрать ненужный фон вокруг фигуры.
Для слоев с боковыми гранями верните Opacity=100%.
Видео по теме
Полезный совет
При подборе оттенков цвета для граней учитывайте расположение источника света на вашем изображении
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и все углы равны. Вокруг правильного многоугольника можно описать окружность. Именно эта окружность и помогает в его построении. Одним из правильных многоугольников, построение которого можно сделать с использованием простейших инструментов, является правильный пятиугольник.
Вам понадобится
- линейка, циркуль
Инструкция
Далее через точку O проведите прямую, перпендикулярную прямой OA. Построить перпендикулярную прямую можно с помощью угольника или (методом двух окружностей одинакового радиуса). Ее пересечение с окружностью можно обозначить за точку B.
Постройте на отрезке OB точку C, которая будет являться его серединой. Затем нужно провести окружность с центром в точке C, проходящую через точку A, то есть, радиусом CA. Точку пересечения этой кружности с прямой OB внутри окружности с центром O (или первоначальной окружности) обозначьте за D.
Затем проведите окружность с центром в A через точку D. Ее пересечение с первоначальной окружностью обозначьте за точки E и F. Это будут две вершины прявильного пятиугольника.
Проведите окружность с центром в E через точку A. Обозначьте её пересечение с первоначальной окружностью как точку G. Это будет одна из вершин пятиугольника.
Аналогично проведите окружность с центром в F через точку A.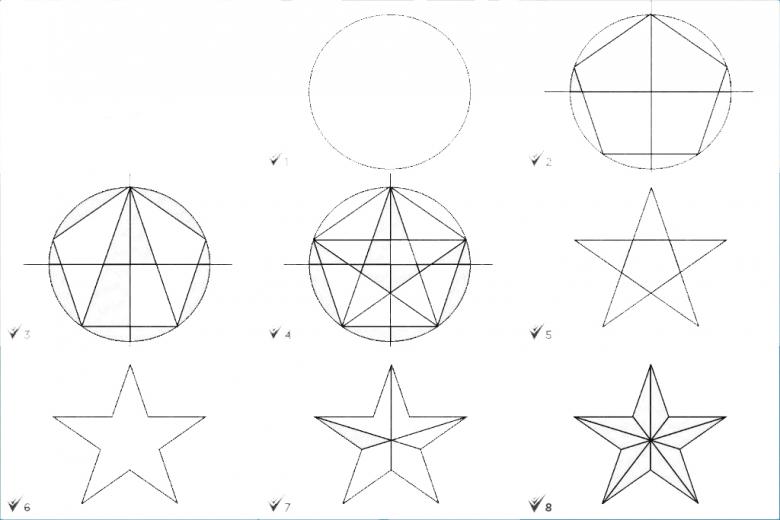 Обозначьте её другое пересечение с первоначальной окружностью как точку H. Эта точка также будет вершиной прямоугольника.
Обозначьте её другое пересечение с первоначальной окружностью как точку H. Эта точка также будет вершиной прямоугольника.
Затем соедините точки A, E, G, H и F. В результате получится правильный пятиугольник, вписанный в окружность.
Видео по теме
Шестиугольником называют частный случай полигона — фигуры, образованной множеством точек плоскости, ограниченным замкнутой полилинией. Правильный шестиугольник (гексагон), в свою очередь, также является частным случаем — это полигон с шестью равными сторонами и равными углами. Эта фигура примечательна тем, что длина каждой из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — лист бумаги.
Инструкция
Выберите длину стороны . Возьмите циркуль и установите расстояние концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на другой ножке, равным длине стороны вычерчиваемой фигуры.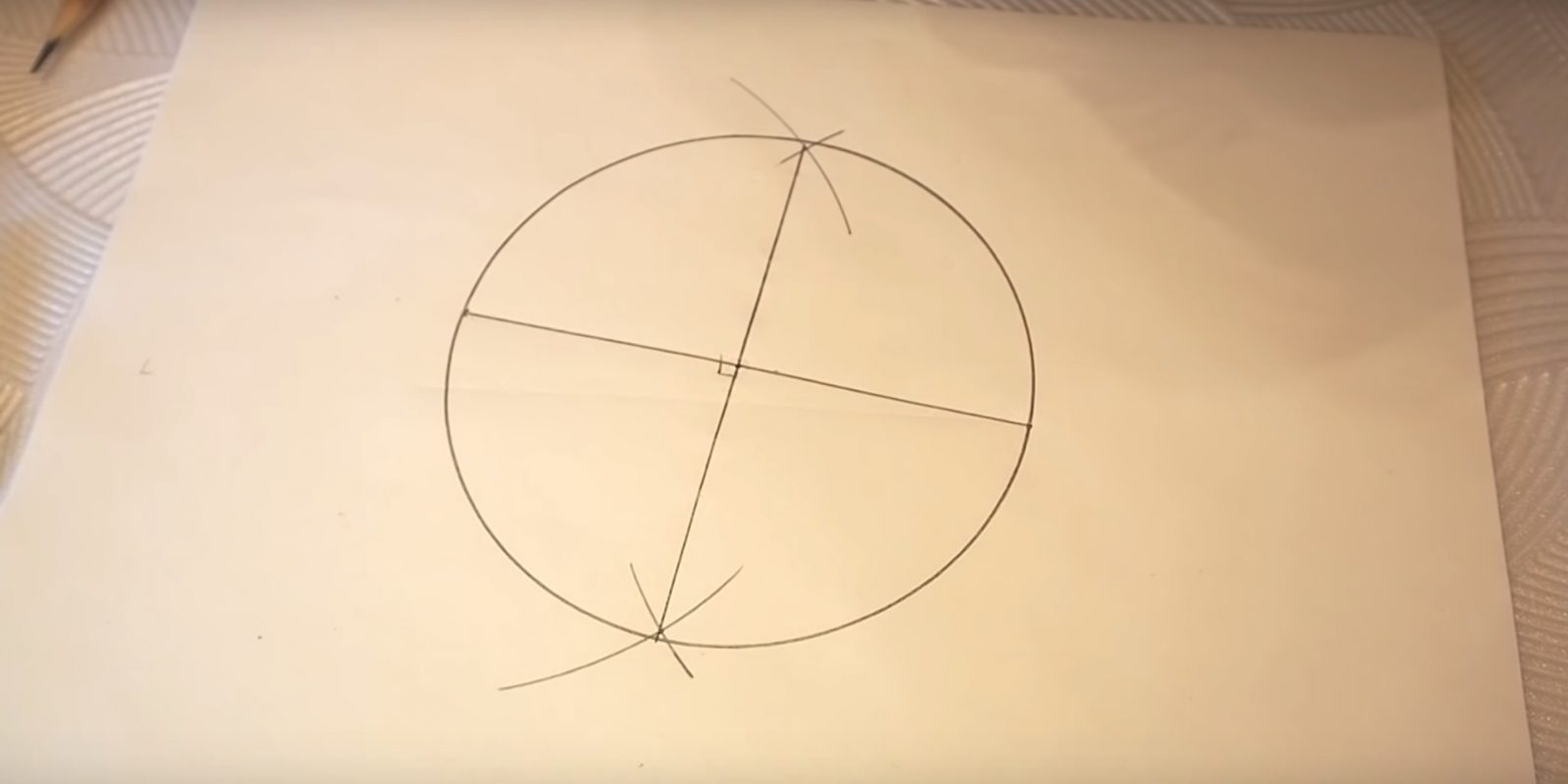 Для этого можно воспользоваться линейкой либо выбрать случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая возможность.
Для этого можно воспользоваться линейкой либо выбрать случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая возможность.
Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна точно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, чтобы она пересекла в двух точках окружность, начерченную первой.
Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с первоначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в двух точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
Подобным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении вдоль окружности (всегда по или против часовой стрелки). В результате должны быть выявлены шесть точек пересечения дуг с первоначально построенной окружностью.
В результате должны быть выявлены шесть точек пересечения дуг с первоначально построенной окружностью.
Нарисуйте правильный шестиугольник. Последовательно попарно соедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В результате будет получен правильный шестиугольник. После осуществления построения можно стереть вспомогательные элементы (дуги и окружность).
Обратите внимание
Имеет смысл выбирать такое расстояние между ножками циркуля, чтобы угол между ними был равен 15-30 градусов, иначе при осуществлении построений данное расстояние может легко сбиться.
В свое время процесс черчения правильного шестиугольника был описан еще древним греком Евклидом. Однако на сегодняшний день существуют и другие способы построения этой геометрической фигуры. Главный принцип – придерживаться при черчении фигуры некоторых известных правил.
Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
Вам понадобится
- – линейка
- – циркуль
Инструкция
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.
3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Инструкция
1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).
3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .
4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.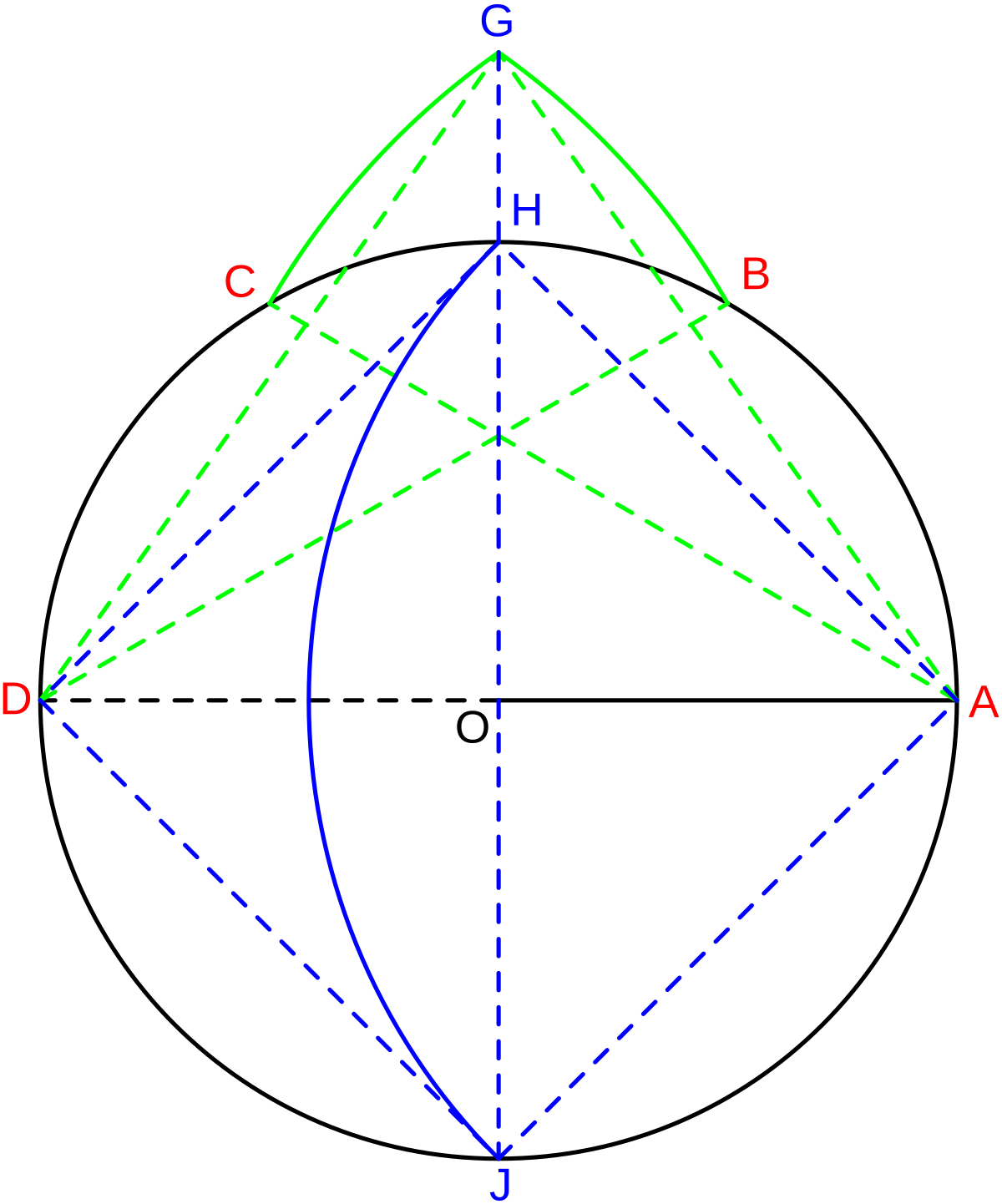 Точки G,E,B,F,H – вершины положительного пятиугольника .
Точки G,E,B,F,H – вершины положительного пятиугольника .
5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.
6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.
Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .
3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.
4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Видео по теме
Луч — это прямая линия, проведенная из точки и не имеющая конца.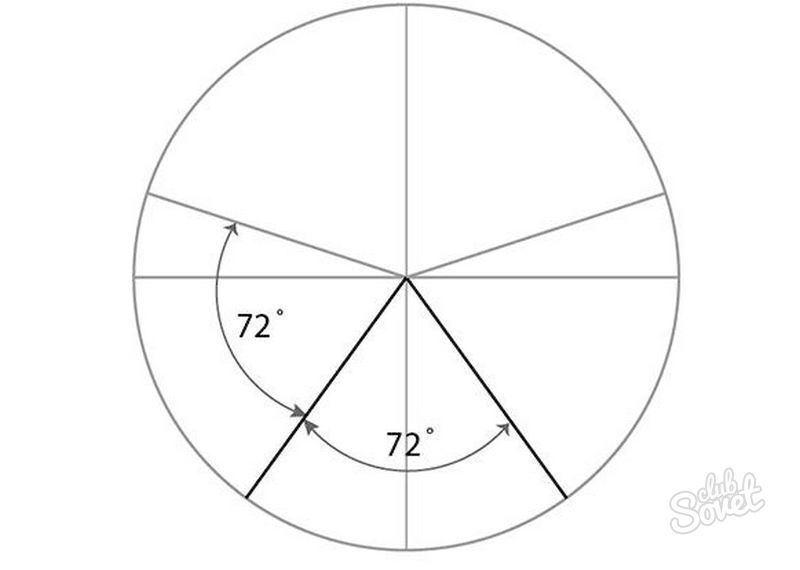 Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.
2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.
5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.
6. Луч благополучно нарисован и заняло это каждого несколько минут.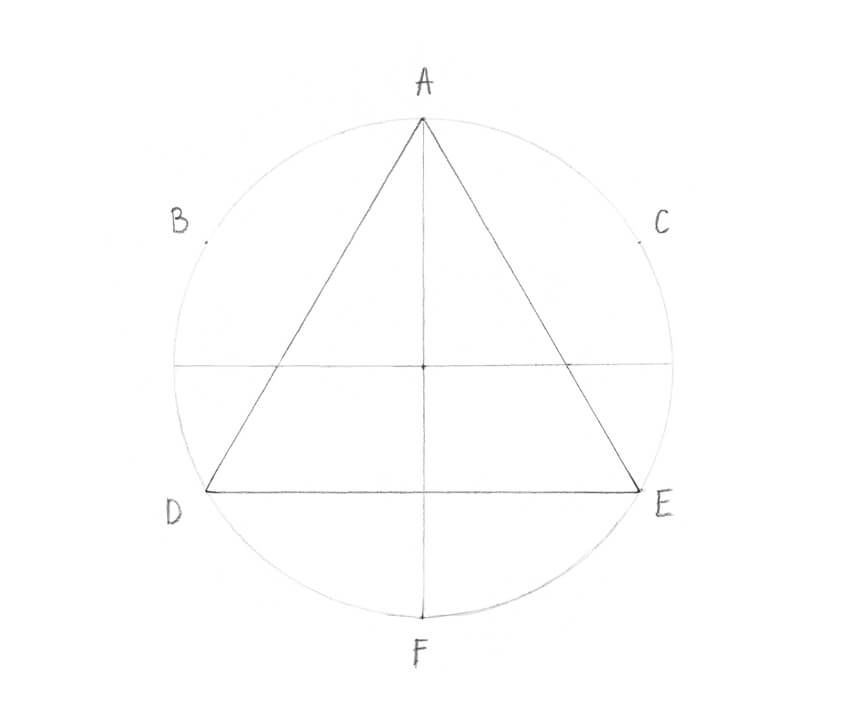 Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Видео по теме
Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.
Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.
Как нарисовать звезду — Пошаговое руководство по рисованию самой простой пятиконечной звезды
Это должен быть самый простой и безотказный метод рисования звезды. Ну не один метод, а 2 безумно простых. Следуйте пошаговым инструкциям и начните рисовать звезды в кратчайшие сроки.
Я решил предложить вам 2 разных способа рисования направляющих звезд, классическую звезду «одним мазком», а также мою упрощенную версию этого метода (идеально подходит для детей и всегда дает идеальную звезду). Оба урока покажут вам, как нарисовать 5-конечную звезду.
Оба урока покажут вам, как нарисовать 5-конечную звезду.
*данный пост содержит партнерские ссылки*
Звезда — одна из тех базовых фигур, которая очень удобна при обучении рисованию, поскольку ее можно использовать для улучшения многих ваших рисунков. Рисунок единорога — прекрасный пример, так как он будет выглядеть еще более волшебно, когда его окружает множество сверкающих замечательных звезд.
Как нарисовать звезду – пятиконечная звезда
Что вам нужно:
- одно из наших руководств по рисованию звезд (дополнительно)
- карандаш или маркер (или оба)
- бумага
- дополнительно: ластик
Версия 1: Самый простой способ нарисовать идеальную звезду
Мы очень рады поделиться с вами этим уроком, так как это самый простой способ нарисовать идеальную звезду! И всего 4 шага! Вы можете нарисовать его карандашом и обвести конечный рисунок маркером, или просто оставить как есть, со всеми линиями — ведь такие звезды и так выглядят довольно круто.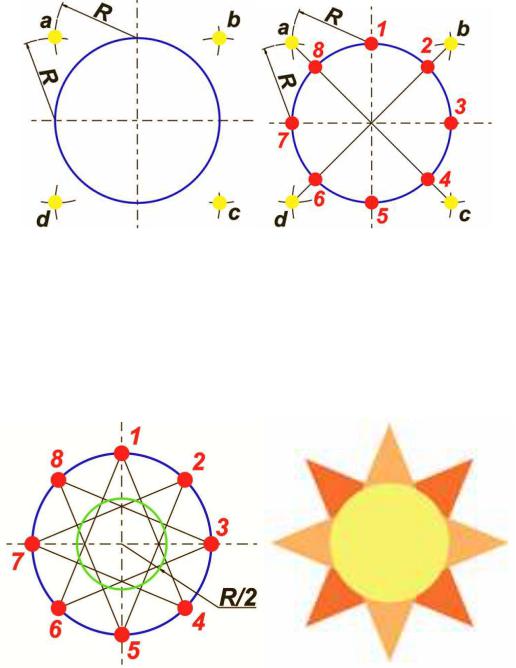
Шаг 1
Начните с рисования буквы А без горизонтальной линии.
Шаг 2
Нарисуйте горизонтальную линию в верхней трети буквы «А».
Шаг 3
Почти готово, осталось всего два штриха карандаша. Все, что осталось сделать, это «соединить точки», провести линию от одного конца горизонтальной линии, скажем, слева, до нижнего правого конца «буквы А».
Шаг 4
Проделайте то же самое с другой стороной.
Поздравляем, вы научились рисовать звезду! Теперь вы можете обвести его маркером и стереть линии или проявить творческий подход и придать своей звезде смайлик.
Версия 2: Рисование звезды одним мазком
Вам не нужно отрывать ручку от бумаги, чтобы нарисовать звезду этим методом. Как только вы освоитесь, это самый быстрый способ рисования звезд.
Вы можете рисовать карандашом, а когда закончите, обведите внешние линии маркером, чтобы получилась идеальная звезда без линий внутри.
Шаг 1
Начните с рисования горизонтальной линии слева направо.
Шаг 2
Продолжайте рисовать линию под углом.
Шаг 3
Следующая линия должна идти под углом и до верха рисунка звезды.
Шаг 4
Вы почти у цели! Теперь проведите линию сверху вниз, опять же под углом.
Шаг 5
Теперь осталось только соединить последнюю линию с первой, и вы нарисовали звезду.
Шаг 6
Если рисуете карандашом, обведите рисунок маркером и сотрите карандаш.
Получите печатные чертежи Star Directed здесь
Версия 1: Руководство по рисованию звезд, версия 1
Версия 2: Руководство по рисованию звезд, версия 2
Счастливый рисунок
Разблокируйте VIP-распечатки — станьте участником
Станьте участником программы Easy Peasy and Fun и получите доступ к нашим эксклюзивным шаблонам для творчества и образовательным печатным материалам.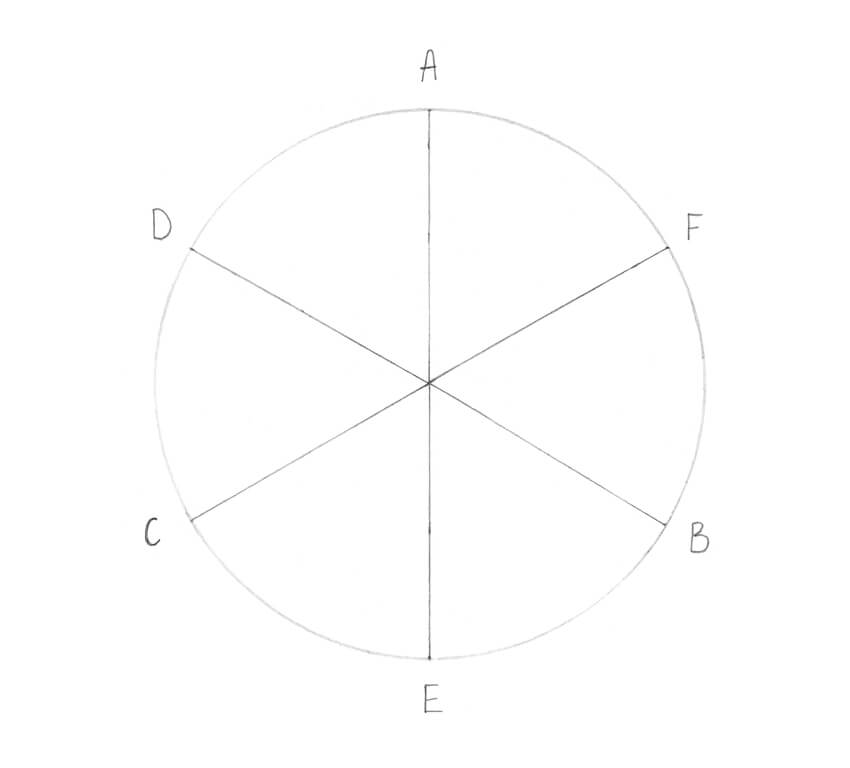 Благодаря еженедельному добавлению новых ресурсов у вас никогда не закончатся забавные вещи, которые можно сделать со своими детьми (будь то родитель или учитель).
Благодаря еженедельному добавлению новых ресурсов у вас никогда не закончатся забавные вещи, которые можно сделать со своими детьми (будь то родитель или учитель).Как рисовать звезды и звезду Давида с помощью простых пошаговых уроков рисования и руководств для детей
Как рисовать пятиконечные звезды
Хочешь учиться как нарисовать пятиконечные звезды? Если вы не умеете рисовать звезды, но тогда это пошаговое руководство поможет вам разобраться как нарисовать пятиконечную звезду, используя круг и стрелки для построения форма.
Как легко нарисовать шестиконечные морские звезды
Следуйте дальнейшим пошаговым инструкциям, и вы сможете легко рисовать его в будущем.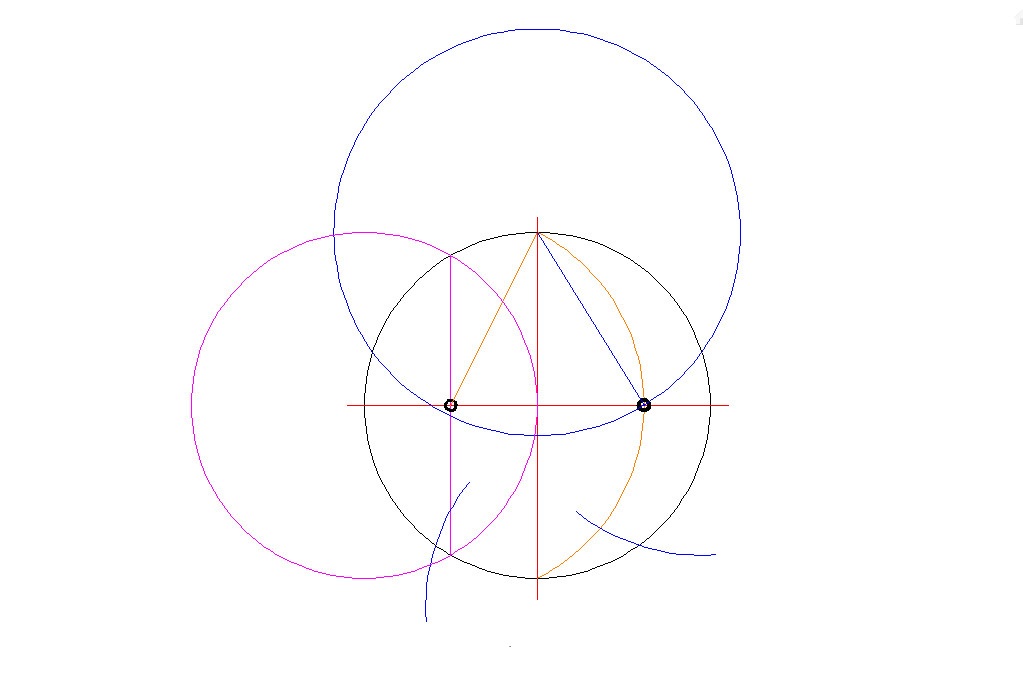
Как нарисовать причудливую звезду Давида
Научитесь рисовать Звезду Давида, также известную как Еврейская Звезда.
Научитесь рисовать звезду Марио
Сегодня мы покажем вам, как нарисовать Звезду из Super Mario Bros от Nintendo. Узнайте, как нарисовать Звезду с помощью следующего простого пошагового руководства.
Как Нарисовать звезду
А пятиконечная звезда так полезна.Вы можете использовать его, чтобы рисовать картинки, делать дизайн канцелярских принадлежностей или украшение открыток для праздничных мероприятий. это также отлично подходит для учителей, которые могут использовать его для оценки работ или для создания картонная форма для вручения призов или подвески в качестве мобильного телефона.
это также отлично подходит для учителей, которые могут использовать его для оценки работ или для создания картонная форма для вручения призов или подвески в качестве мобильного телефона.
Как нарисовать морскую звезду
Позволяет начните этот первый шаг, нарисовав несколько простых линий, которые помогут Вы рисуете морскую звезду намного лучше.
Как нарисовать звезду
Там Есть два способа нарисовать звезду: с помощью циркуля, линейки и транспортира или свободной рукой. Линейка и циркуль помогут вам нарисовать 90 169 с точностью. – идеальная пятиконечная звезда или любая звезда, которую вы хотите.
Линейка и циркуль помогут вам нарисовать 90 169 с точностью. – идеальная пятиконечная звезда или любая звезда, которую вы хотите.
Как нарисовать звезду Давида, Вифлеемскую звезду
Техника рисования звезды Давида.
Как нарисовать звезду Давида
звезда Давида, также известная как «еврейская звезда». в основном два треугольника друг над другом.Эта статья покажет вы, как нарисовать эту звезду.
Как рисовать мультяшных звезд
Рисунок мультипликационные звезды: несколько забавных фактов перед тем, как начать рисовать!
Как легко нарисовать Звезду Давида.
 Учебник и Раскраска Звезда Давида · Художественные проекты для детей
Учебник и Раскраска Звезда Давида · Художественные проекты для детейУзнайте, как нарисовать еврейскую звезду Давида, сделав два треугольника так, как будто они обернуты друг вокруг друга.
Звезда Давида Учебник
Раскраска Звезда Давида
Раскраска Звезда Давида
Звезда Давида или Маген Давид (буквально «Щит Давида»), как ее называют на иврите, сегодня является наиболее распространенным символом для выражения еврейской идентичности. Еврейское название символа — гексаграмма, образованная двумя перекрывающимися треугольниками, один направлен вверх, а другой — вниз, — происходит от его предполагаемого сходства со щитом царя Давида.
В этом пошаговом руководстве учащимся показано, как нарисовать более сложную версию Звезды Давида, в которой два треугольника выглядят так, как будто они сплетены вместе. В основном им нужно перекрыть два равносторонних треугольника, а затем стереть несколько ключевых линий. Немного математики встречается с искусством и еврейской историей!
В основном им нужно перекрыть два равносторонних треугольника, а затем стереть несколько ключевых линий. Немного математики встречается с искусством и еврейской историей!
Используйте кнопку ниже, чтобы загрузить учебник в формате PDF
Открыть учебник по рисованию звезды ДавидаРаскраска Звезда Давида
Откройте страницу раскраски Звезда ДавидаМатериалы для рисования звезды Давида
- Ластик. Большие карандаши, которые можно держать в руке, работают гораздо лучше, чем просто кончики карандашей.
- Черный Маркер Sharpie . Эти перманентные маркеры с тонким концом создают красивые черные контуры, имеют хороший наконечник для окрашивания и никогда не растекаются, когда намокают. Используйте их с хорошей вентиляцией и подложите под них дополнительную бумагу, чтобы защитить столы.
- Мелки Prang .
 Они немного мягче, чем другие мелки, поэтому иногда выглядят как масляная пастель.У них также есть несколько приятных коричневых оттенков, которых нет у Crayola, если только вы не купите их большие коробки.
Они немного мягче, чем другие мелки, поэтому иногда выглядят как масляная пастель.У них также есть несколько приятных коричневых оттенков, которых нет у Crayola, если только вы не купите их большие коробки.
- Мелки Crayola . Надежный бренд, который всегда работает хорошо. В наборе из 24 штук одни из моих любимых золотисто-оранжевых и желтых цветов, которые кажутся немного богаче и теплее, чем те, что есть у Прэнг.
Указания по рисованию звезды Давида шаг за шагом
Необходимое время: 25 минут.
Как нарисовать звезду Давида
- Нарисуйте равносторонний треугольник.
Делайте СВЕТЛЫЕ линии на протяжении всего урока, чтобы их было легко стирать. - Нарисуйте еще один треугольник, повернутый, как показано на рисунке.
- Контур с большим треугольником.
- Обведите еще одним большим треугольником.

- Сотрите две пары линий, как показано на рисунке.
- Сотрите две пары линий, как показано на рисунке.
- Сотрите две пары линий, как показано на рисунке.
- Звезда готова.
- Обведите маркером и цветом.
Как нарисовать звезду шаг за шагом — для детей и начинающих
Желаю всем вам сиять как звезда, поэтому мы научимся рисовать звезду простыми шагами. Звезда — одна из самых простых и удобных форм. Звезды используются для обозначения блеска, неба, небес. В основном пятиконечная звезда используется в рисовании и во многих случаях.
Ислам, бахаи и многие религии используют его как религиозный символ. С другой стороны, в Европе это символ власти и авторитета. Звезда симметричная, образует заостренную структуру, 3, 4, 5, 6, 7 точек. Это полностью зависит от вас, как вы хотите это нарисовать.
5-конечная звезда в основном используется и рисуется всеми. В этом уроке мы покажем, как нарисовать 5-конечные звезды, 6-конечные звезды, мультяшные звезды и звезду Давида. Узнайте больше о простых рисунках, следуя другим нашим статьям.
Как нарисовать пятиконечную звезду:
Научитесь рисовать 5-конечную звезду, используя приведенные ниже шаги, за ними очень легко следовать, так как вам нужно только рисовать линии.
Шаг 1: Нарисуйте, начав противоположную букву V внутрь, как показано на рисунке ниже.
Шаг 2: Проведите горизонтальную линию из середины нарисованной буквы V.
Шаг 3: Соедините левый конец горизонтальной линии с правым концом внутренней буквы V.
Шаг 4: Соедините правый конец линии с левым концом V.
Ваша пятиконечная звезда готова благодаря этим очень простым шагам.
Нарисуйте шестиконечную звезду:
Приготовьтесь нарисовать 6-конечную звезду и возьмите компас, карандаш, линейку и сотрите, чтобы начать рисовать.
Шаг 1: Нарисуйте круг с помощью циркуля.
Шаг 2: Начертите 2 перпендикулярных диаметра круга.Назовите их A, B, C, D
Шаг 3: Нарисуйте точки B, C, D, E между четвертями, образованными диаметрами чертежа.
Шаг 4: Соединив точки A, D, E, нарисуйте равносторонний треугольник.
Шаг 5: Затем из точек F, B, C нарисуйте еще один треугольник, как показано на рисунке ниже.
Как нарисовать звезду Давида:
Звезда Давида — это гексаграмма, также называемая Щитом Давида, давайте начнем рисовать.
Шаг 1: Нарисуйте маленький треугольник.
Шаг 2: Нарисуйте еще один противоположный треугольник, перекрывающий первый.
Шаг 3: Поверх этого нарисуйте еще один большой треугольник.
Шаг 4: Нарисуйте еще один большой нисходящий треугольник.
Шаг 5: Как показано на рисунке ниже, сотрите 2 строки.
Шаг 6: Сотрите снова 2 строки, как показано на рисунке ниже.
Шаг 7: До этого шага звезда Давида завершена.
Шаг 8: Раскрасьте свою звезду соответствующим образом.
Как нарисовать Мультяшную звезду:
Мультфильмы всегда привлекают детей, почему бы не нарисовать звездный мультфильм, следуйте приведенным ниже шагам, и он будет с вами.
Шаг 1: Нарисуйте пятиконечную звезду, которую вы узнали на предыдущем шаге.
Шаг 2: С обеих сторон звезды нарисуйте руки, используя 2 руки с множеством кривых, образующих облако.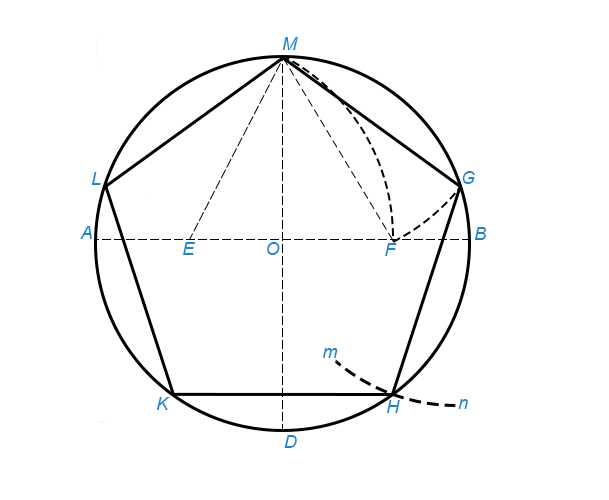
Шаг 3: Внутри начала нарисуйте глаза тремя овалами, брови двумя прямоугольниками, нарисуйте 1 большой овал линией внизу.
Шаг 4: Нарисуйте ноги в нижней части.
Шаг 4: Раскрасьте звезду соответствующим образом или как показано на изображении ниже.
Рисование мультяшной звезды не требует никаких дополнительных навыков, все, что вам нужно сделать, это нарисовать простую звезду и добавить к ней мультяшные глаза и рот.
Ваши сияющие звезды готовы сверкать с помощью этих простых шагов.
ЗВЕЗДА ДАВИДА — Mathemechanix.org
THE ЗВЕЗДА ДАВИДА Страница 49За столетия до Рождества Христова царь Давид правил на Ближнем Востоке, связанном с древнееврейские учения.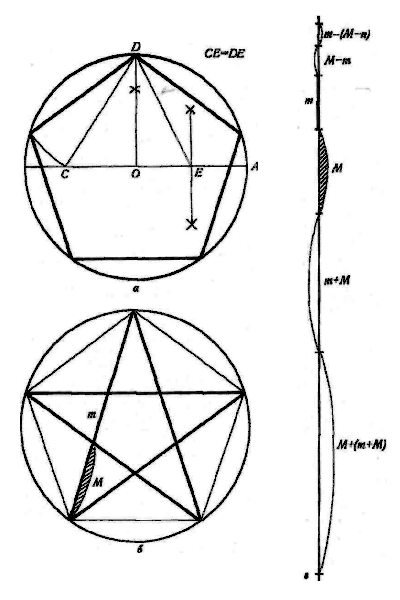 Возможно, лучше всего он известен как убийца Голиафа. Шестиконечная звезда связана с этим королем, правившим около 1000 г. до н.э.С 1948 года Звезда Давида стала символом Израиля на их флаге. РИСУНОК ЗВЕЗДЫ ЗВЕЗДЫ: есть ли какой-нибудь простой способ нарисовать звезду с абсолютно правильными размерами? Во времена царя Давида мало что было известно об алгебре или общей науке об измерениях. То, что обычно практиковалось, больше относилось к сфере плоской геометрии. Ученый-пурист должен создавать все рисунки и фигуры, используя не более чем простой циркуль и линейку.Никаких чисел! Начните с прямой линии. Отметьте точку где-то рядом с центром этой линии. Затем настройте компас на фиксированное значение и никогда не изменяйте эту настройку. Из центральной точки вдоль линии нарисуйте окружность, достаточно большую, чтобы пересечь оба конца линии. Затем нарисуйте второй неполный круг с центром в одной из отметок, только что сделанных на линии. Повторите это для круга, нарисованного вокруг второй отметки.
Возможно, лучше всего он известен как убийца Голиафа. Шестиконечная звезда связана с этим королем, правившим около 1000 г. до н.э.С 1948 года Звезда Давида стала символом Израиля на их флаге. РИСУНОК ЗВЕЗДЫ ЗВЕЗДЫ: есть ли какой-нибудь простой способ нарисовать звезду с абсолютно правильными размерами? Во времена царя Давида мало что было известно об алгебре или общей науке об измерениях. То, что обычно практиковалось, больше относилось к сфере плоской геометрии. Ученый-пурист должен создавать все рисунки и фигуры, используя не более чем простой циркуль и линейку.Никаких чисел! Начните с прямой линии. Отметьте точку где-то рядом с центром этой линии. Затем настройте компас на фиксированное значение и никогда не изменяйте эту настройку. Из центральной точки вдоль линии нарисуйте окружность, достаточно большую, чтобы пересечь оба конца линии. Затем нарисуйте второй неполный круг с центром в одной из отметок, только что сделанных на линии. Повторите это для круга, нарисованного вокруг второй отметки. Сделайте отметки в 4 точках, где пересекаются три круга. Есть 6 отмеченных точек.(На рисунке мы не нарисовали полные окружности. Достаточно коротких дуг. Мы показываем все эти дуги.) Далее проводим прямые линии из одной точки в другую, но пропуская точку. Сделайте это для точек, на которые нет первой ссылки. У вас получится два равносторонних треугольника. Сотрите все линии, кроме последнего набора равносторонних треугольников. Результатом является Звезда Давида. Также покажите центр первого круга, так как этот знак также имел значение в ранней истории. Создавая звезду, вы определили в общей сложности 6 равносторонних треугольников, включая перевернутые.Углы между сторонами неравностороннего треугольника должны быть равны 60 градусов каждый, а в сумме 180 градусов, как и для треугольников в целом. Центральный (перевернутый) треугольник имеет угол 60 градусов и равные стороны, что означает, что это равносторонний треугольник, и, следовательно, горизонтальная линия на вершине равна по длине любой другой линии.
Сделайте отметки в 4 точках, где пересекаются три круга. Есть 6 отмеченных точек.(На рисунке мы не нарисовали полные окружности. Достаточно коротких дуг. Мы показываем все эти дуги.) Далее проводим прямые линии из одной точки в другую, но пропуская точку. Сделайте это для точек, на которые нет первой ссылки. У вас получится два равносторонних треугольника. Сотрите все линии, кроме последнего набора равносторонних треугольников. Результатом является Звезда Давида. Также покажите центр первого круга, так как этот знак также имел значение в ранней истории. Создавая звезду, вы определили в общей сложности 6 равносторонних треугольников, включая перевернутые.Углы между сторонами неравностороннего треугольника должны быть равны 60 градусов каждый, а в сумме 180 градусов, как и для треугольников в целом. Центральный (перевернутый) треугольник имеет угол 60 градусов и равные стороны, что означает, что это равносторонний треугольник, и, следовательно, горизонтальная линия на вершине равна по длине любой другой линии. Перемещенная линия. Что вам удалось сделать, так это разделить угол на 180 градусов пополам. на три угла по 60 градусов. В общем случае трисекция угла невозможна с помощью чисто геометрических процессов (доказано П.L. Wantzel в 1847 г.). Однако существует несколько частных случаев, таких как этот. (Другой разделяет угол в 270 градусов на три угла по 90 градусов.) Возможно, изобретатели звезды Давида были первыми, кто разделил угол на три части!
Перемещенная линия. Что вам удалось сделать, так это разделить угол на 180 градусов пополам. на три угла по 60 градусов. В общем случае трисекция угла невозможна с помощью чисто геометрических процессов (доказано П.L. Wantzel в 1847 г.). Однако существует несколько частных случаев, таких как этот. (Другой разделяет угол в 270 градусов на три угла по 90 градусов.) Возможно, изобретатели звезды Давида были первыми, кто разделил угол на три части!
Как нарисовать звезду | Пошаговое руководство
Простое пошаговое руководство по рисованию звездыНажмите ЗДЕСЬ, чтобы сохранить урок в Pinterest!
Пятиконечная звезда использовалась как символ во всем мире, охватывающий тысячелетия человеческой цивилизации и пересекающий культурные границы.В самом общем смысле звезда представляет небеса, ночное небо и космическое пространство, где вы также можете увидеть кометы!
В средневековой Европе звезда использовалась для обозначения силы, власти и геральдики. Пятиконечная звезда также используется различными религиями, включая ислам, веру бахаи и религию Серрера в Западной Африке, а также многими военными подразделениями, нерелигиозными обществами, спортивными командами и организациями.
Пятиконечная звезда также используется различными религиями, включая ислам, веру бахаи и религию Серрера в Западной Африке, а также многими военными подразделениями, нерелигиозными обществами, спортивными командами и организациями.
Хотите научиться рисовать идеально симметричную пятиконечную звезду? Теперь вы можете, следуя этому простому пошаговому руководству по рисованию.
Прокрутите вниз, чтобы загрузить PDF-файл этого руководства.
Чтобы нарисовать звезду, вам понадобится лист бумаги и письменные принадлежности, такие как ручка, карандаш или маркер. Вы также можете использовать цветные карандаши, маркеры или мелки, чтобы раскрасить законченный рисунок. Также желательно иметь под рукой хороший ластик и линейку с прямым краем.
Каждый шаг в этом руководстве по рисованию сопровождается иллюстрацией. На каждом изображении новые строки, добавленные на этом шаге, выделены синим цветом; ранее нарисованные линии отображаются черным цветом. Скорее всего, сначала вы захотите рисовать слегка, так как по мере продвижения вы будете стирать некоторые исходные линии.
Скорее всего, сначала вы захотите рисовать слегка, так как по мере продвижения вы будете стирать некоторые исходные линии.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Крылья ангела, Огонь и Череп.
Пошаговые инструкции по рисованию звезды
Рисование звезды — шаг 1Для начала нарисуйте квадрат. Вы можете использовать линейку, чтобы обеспечить прямые линии и прямые углы.
Рисунок звезды — шаг 2Проведите вертикальную линию посередине квадрата. Из этой же точки проведите линию с каждой стороны от первой.Эти линии будут встречаться с нижней частью квадрата между первой линией и сторонами квадрата.
Рисунок звезды — шаг 3Проведите прямую горизонтальную линию через середину квадрата. От каждого конца этой линии протяните прямую линию вниз и к центральной вертикальной линии. Эти линии будут встречаться с вертикальной линией на полпути между горизонтальной линией и нижней частью квадрата.
Рисование звезды — шаг 4 Из точки, где сходились предыдущие линии, проведите еще две линии. Эти линии будут встречаться с нижней частью квадрата в той же точке, что и почти вертикальные линии.
Эти линии будут встречаться с нижней частью квадрата в той же точке, что и почти вертикальные линии.
От двух нижних точек звезды проведите две прямые линии, которые сойдутся в центре звезды.
Рисунок звезды — шаг 6От двух боковых точек звезды проведите две прямые линии, которые сходятся в центре звезды.
Рисунок звезды — шаг 7Проведите прямые линии от каждой точки внутреннего перевернутого пятиугольника к центру звезды.
Рисование звезды — шаг 8Сотрите направляющие линии — как внутри звезды, так и в исходном квадрате.
Рисунок звезды — шаг 9Раскрась свою звезду. Использование двух разных оттенков для чередующегося окрашивания звезды усилит трехмерный эффект звезды.
Учебное пособие по рисованию для печати
УСТРАНЕНИЕ НЕИСПРАВНОСТЕЙ ДЛЯ УЧАСТНИКОВ
Все еще видите рекламу или не можете загрузить PDF-файл?
Во-первых, убедитесь, что вы вошли в систему. Вы можете войти на странице входа участника.
Если вы по-прежнему не можете загрузить PDF-файл, вероятное решение — перезагрузить страницу.
Это можно сделать, нажав кнопку перезагрузки браузера.
Это значок в виде круглой стрелки в верхней части окна браузера, обычно расположенный в верхней левой части (вы также можете использовать сочетания клавиш: Ctrl+R на ПК и Command+R на Mac).
Как сделать золотой компас в Illustrator
Preview
Инструментом «Эллипс» (L) создайте круг.
Применим к этой новой окружности радиальный градиент.
Поскольку компас считается устаревшим, нам нужно выбрать соответствующие цвета.
Дублируйте круг, скопировав его (Ctrl/Cmd + C) и вставив на передний план (Ctrl/Cmd + F).
Затем перейдите в Объект > Трансформировать > Масштаб.
Примените радиальный градиент, как показано ниже. Установите цвет обводки на #B89534.
Выберите два объекта и сгруппируйте их, нажав Ctrl/Cmd + G.
Шаг 2: Создание шагов компаса должны рассчитать угол поворота для приращений, чтобы наша работа была точной.

Давайте решим, что будем создавать три разных шага.
Первый и самый большой набор приращений будет 20 o за приращение, начиная с 0 o , 20 o , 40 o , 60 o и так далее.
Это означает, что нам нужно 18 приращений, чтобы сделать полный оборот (360 o / 18 = 20 o приращений).
Возьмите инструмент «Линия» (/) на панели инструментов и нарисуйте небольшую вертикальную линию. Совместите его с корпусом с помощью кнопки Horizontal Align Center под панелью выравнивания.
Удерживая нажатыми клавиши Alt/Opt + Shift, щелкните и перетащите линию вниз. Alt/Option создает дубликат перетаскиваемого объекта, а Shift ограничивает движение по вертикали.
Выберите обе строки и сгруппируйте их (Ctrl/Cmd + G).
Затем перейдите в Объект > Трансформировать > Повернуть. Установите Угол на 20 o (как мы рассчитали).
Нажмите кнопку «Копировать» в диалоговом окне «Поворот», чтобы создать копию двух линий, повернутую на 20 o .
После этого у вас должно быть 4 строки.
Повторите трансформацию поворота, выбрав Transform > Transform Again (или нажмите Ctrl/Cmd + D), пока не завершите весь круг.
Теперь давайте создадим новый набор меньших приращений с шагом 10 или .
На этот раз нам нужно создать 36 приращений (360 o / 36 = 10 o приращений).
Для начала разгруппируйте первую пару созданных нами линий, выделив их группу и нажав Ctrl/Cmd + Shift + G (сочетание клавиш Объект > Разгруппировать).
Дублируйте верхнюю линию и уменьшите ее примерно до 1/3 длины.
Удерживая нажатыми клавиши Alt/Opt + Shift, щелкните и перетащите линию вниз, чтобы продублировать ее.
Сгруппируйте две строки, нажав Ctrl/Cmd + G, пока они обе выделены. Затем выберите Object > Transform > Rotate, установив угол на 10 o .
Нажмите кнопку «Копировать», чтобы создать копию двух линий, повернутых на 10 o . Нажимайте Ctrl/Cmd + D, пока не закончите весь круг.
Некоторые меньшие приращения будут перекрывать большие.
Выберите все линии, которые перекрываются с большими шагами, а затем нажмите Delete, чтобы удалить их.
Теперь нам нужны еще меньшие приращения. Мы создадим набор из 2 o приращений.
Этот набор приращений будет немного тоньше, чем более крупные приращения. Нам нужно 180 таких меньших приращений (360 o /180 = 2 o приращений).
Давайте продублируем самое большое приращение.
Нам придется еще больше уменьшить масштаб и изменить значение ширины обводки на 0,5.
Чтобы создать их, просто повторите процесс, который мы использовали для двух других наборов приращений.
Не забудьте удалить перекрывающиеся приращения.
Шаг 3: Создание чисел
Давайте создадим несколько чисел на циферблате компаса для обозначения градусов. Мы просто создадим числа для 10 o , 30 o , 50 o и так далее.
Выберите внутренний круг корпуса компаса, а затем продублируйте его.
Уменьшите копию и удалите цвет заливки и обводки.
Возьмите инструмент «Текст по контуру» на панели инструментов и щелкните контур круга. Введите числа для средних приращений (10 o , 30 o и т. д.).
Выберите красивый шрифт, который дополнит нашу старинную тему старого мира; Я использовал Times New Roman.
Шаг 4: Создание стрелки компаса
Теперь нам нужна стрелка компаса. Он будет иметь красно-синюю цветовую гамму.
Мы будем использовать Star Tool, чтобы нарисовать первоначальную форму.
Возьмите его и щелкните где-нибудь на монтажной области, чтобы открыть диалоговое окно «Звезда». Установите Points на 3 (что создаст треугольник) и нажмите OK.
Инструментом «Удалить опорную точку» (-) удалите средние опорные точки треугольника.
Выберите инструмент «Прямое выделение» (A), щелкните верхнюю опорную точку треугольника, чтобы выбрать ее, и, удерживая клавишу Shift, чтобы ограничить корректировку, перетащите опорную точку вверх.
Возьмите инструмент Линия (/) и нарисуйте вертикальную линию. Совместите его с треугольником, используя кнопку Horizontal Align Center на панели Align.
Нажмите кнопку Разделить на панели Обработки контуров, чтобы разделить иглу пополам. Разгруппируйте получившуюся фигуру. Установите цвет заливки для левой части на темно-красный, а для правой части установите цвет заливки на светло-красный.
Выберите обе части и перейдите в Object > Transform > Reflect. Выберите «Горизонтальное отражение» в диалоговом окне, а затем нажмите кнопку «Копировать».
Выберите обе части, удерживайте Alt/Option + Shift, затем перетащите вниз, чтобы создать копию.
Измените цвет заливки копий на темно-синий (слева) и светло-синий (справа).
Сгруппируйте все части игл, а затем масштабируйте группу, чтобы она соответствовала компасу. Немного поверните его и поместите в середину компаса.
Дублируйте иглы и просто переместите их за пределы монтажной области, так как мы будем использовать эту копию позже.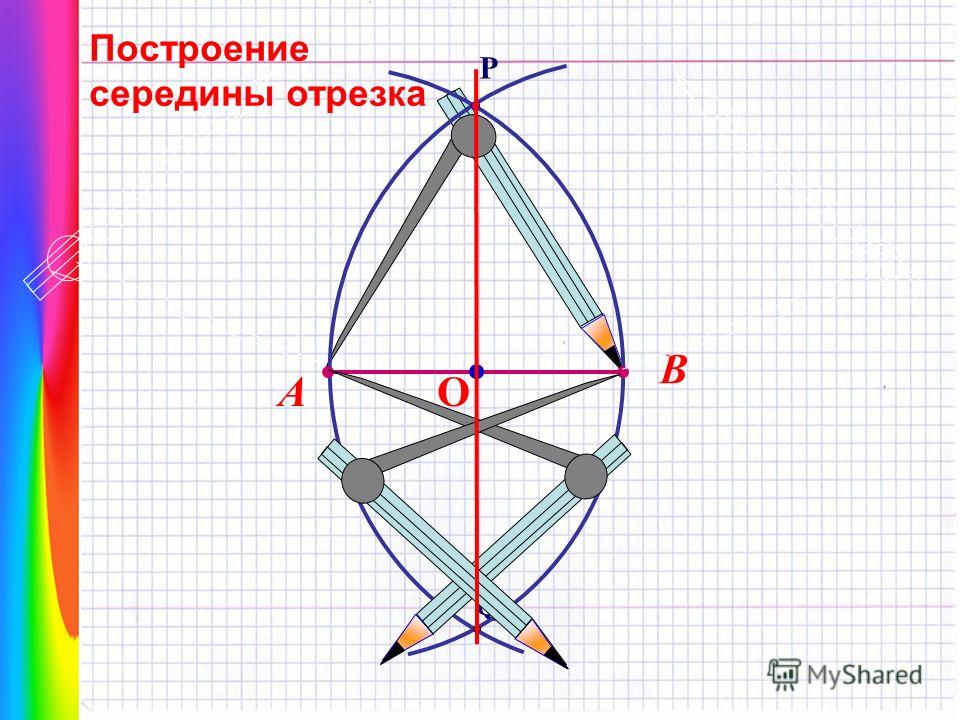
Шаг 5: Создание иглодержателя
Далее мы создадим деталь, удерживающую иглы; он будет размещен прямо в центре игл.Инструментом «Эллипс» (L) создайте два маленьких круга друг над другом. Примените тот же радиальный градиент, который мы использовали для корпуса компаса.
Поместите его в центр игл.
Шаг 6. Создайте розу ветров
Давайте создадим розу ветров (также известную как роза ветров).
Используйте копию иглы, которую мы создали ранее, в качестве отправной точки. Сначала мы удалим нижнюю часть иглы.
Давайте изменим цвета заливки деталей. Я использовал цвета #9B8579 и #C2B59B.
Выберите инструмент «Прямое выделение» (A) на панели инструментов и выберите две опорные точки в центре нижней части объекта.
Удерживая нажатой клавишу Shift, щелкните и перетащите опорные точки вниз.
Перейдите в Object > Transform > Reflect, выберите Horizontal для опции Axis, а затем нажмите кнопку Copy.
Удерживая нажатыми клавиши Alt/Option + Shift, перетащите копию вниз.
Выберите оба объекта и сгруппируйте их (Ctrl/Cmd + G). Перейдите в Object > Transform > Rotate, установите Angle на 90 o , затем нажмите Copy.
Выделите все объекты и сгруппируйте их (Ctrl/Cmd + G).
Дублируйте группу и поверните дубликат на 45 o , а также уменьшите масштаб. Затем поместите его под иглу.
Нам также нужно добавить отметки N, S, E и W на нашу компасную розу.
Несколько раз продублируйте внутренний круг корпуса компаса, удалите цвет заливки и добавьте цвет обводки. Уменьшайте масштаб каждой копии по-разному.
Сгруппируйте все созданные нами элементы (Ctrl/Cmd + G).
Шаг 7: Создайте ромбовидный узор вокруг стороны компаса
Возьмите Инструмент «Прямоугольник» (М) и создайте крошечный прямоугольник. Поверните его на 45 o и поместите на компас. Выровняйте прямоугольник по компасу с помощью кнопки Horizontal Align Center под панелью выравнивания.
Удерживая нажатой клавишу Alt/Opt, щелкните и перетащите прямоугольник вниз.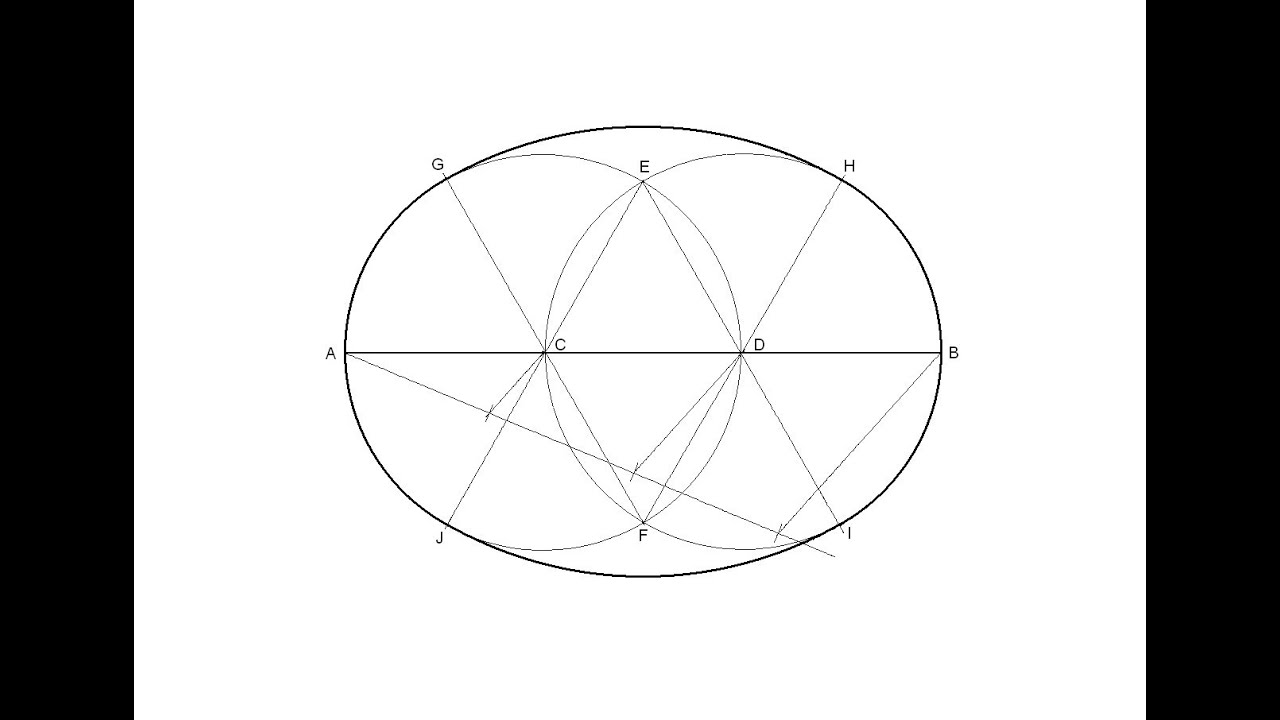
Выберите «Объект» > «Трансформировать» > «Повернуть». Установите Угол на 20 o .
Повторяйте преобразование вращения, нажимая Ctrl/Cmd + D, пока не завершите весь круг.
Шаг 8: Создание отражения в стекле
Каждый компас должен иметь стеклянную крышку. Чтобы имитировать этот вид, мы должны создать отражение окна.
Дублируйте внутренний круг компаса и немного уменьшите его.
Поместите его на вершину стека слоев, выбрав Объект > Упорядочить > На передний план.
Инструментом «Прямое выделение» (А) удалите опорные точки, выделенные ниже.
Возьмите Pen Tool (P) и нарисуйте фигуру, показанную ниже.
Затем с помощью Pen Tool нарисуйте два изогнутых пути через розовый объект, который мы только что нарисовали.
Выберите оба пути и выберите «Объект» > «Разобрать». Удерживая Shift, кликните по розовому объекту, чтобы выделить его и контуры, затем на панели Pathfinder нажмите кнопку Minus Front .
Измените заливку результирующего объекта на радиальный градиент (от прозрачного до белого).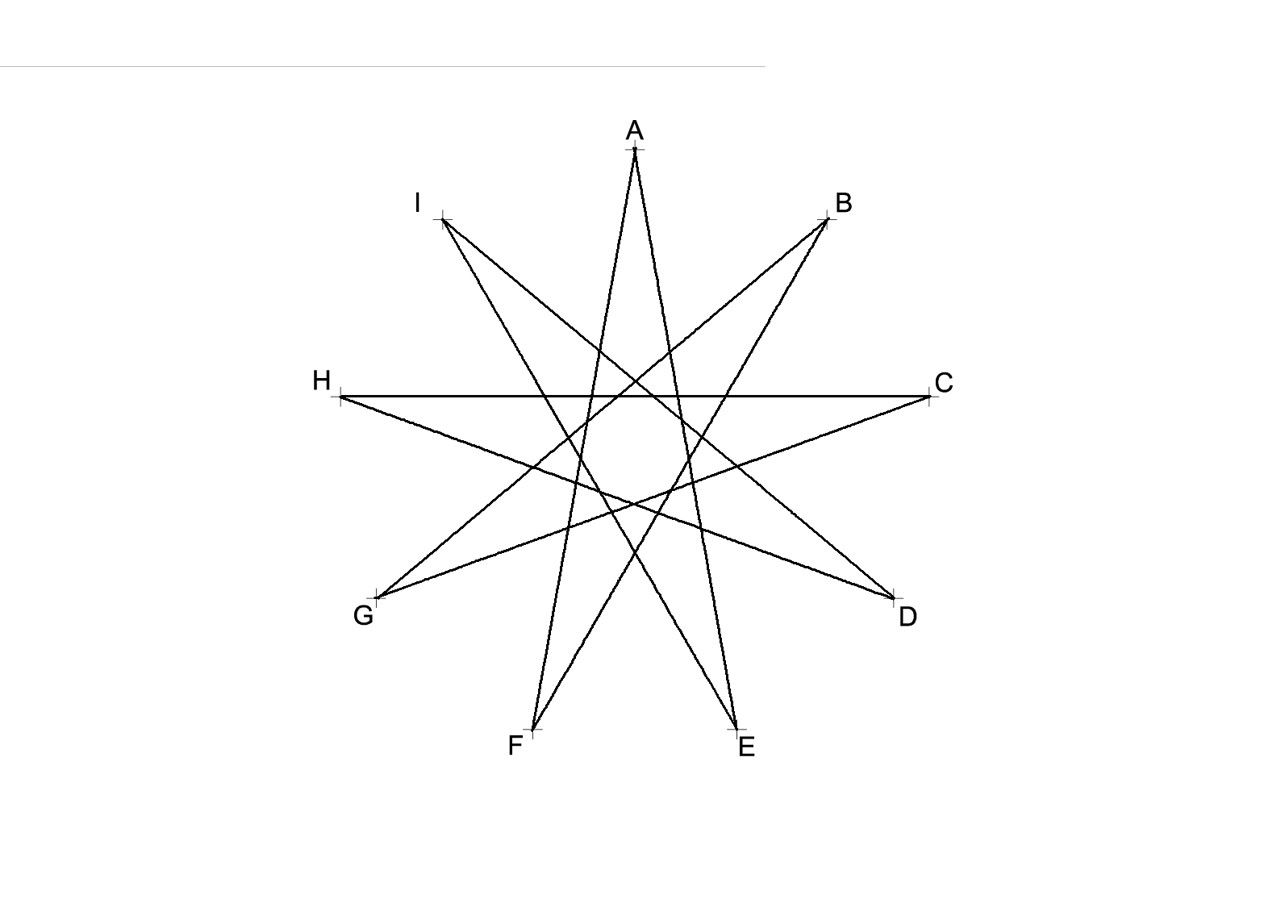
Шаг 9: Добавьте отражение света на металлическом корпусе
Есть еще одна вещь, которую мы можем сделать, чтобы правильно проработать детали.Дублируйте самый большой круг дважды. Переместите одну из копий вниз.
Выделив обе копии, нажмите кнопку Minus Front на панели Pathfinder.
Примените линейный градиент, показанный ниже, чтобы имитировать отражение света на металлическом корпусе.
Краткое изложение урока
Готово! Мы создали, казалось бы, сложную векторную иллюстрацию, используя простые приемы и инструменты, с которыми справятся даже те, кто только начинает работать с Illustrator. Поэкспериментируйте с конечным результатом, используя различные градиенты, цвета и формы.
Вот задание: попробуйте создать версию компаса из серебра/нержавеющей стали (а затем опубликуйте свою работу в комментариях ниже).
Надеюсь, вы получили такое же удовольствие от этого урока, как и я, создавая его для вас. Спасибо!
compass_illustrator (ZIP, 0,99 МБ) .

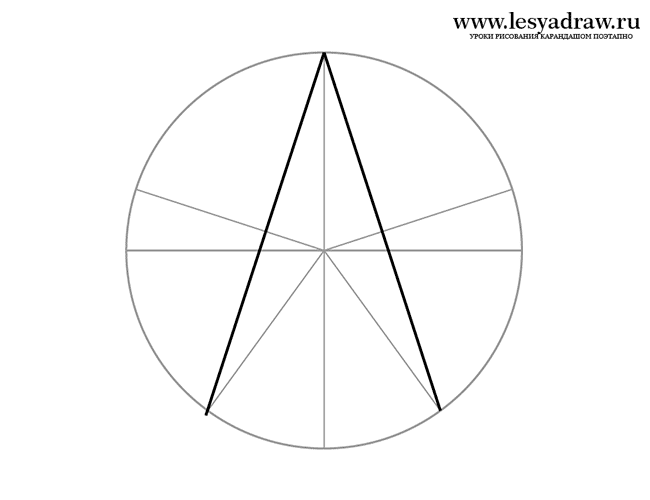
 Они немного мягче, чем другие мелки, поэтому иногда выглядят как масляная пастель.У них также есть несколько приятных коричневых оттенков, которых нет у Crayola, если только вы не купите их большие коробки.
Они немного мягче, чем другие мелки, поэтому иногда выглядят как масляная пастель.У них также есть несколько приятных коричневых оттенков, которых нет у Crayola, если только вы не купите их большие коробки.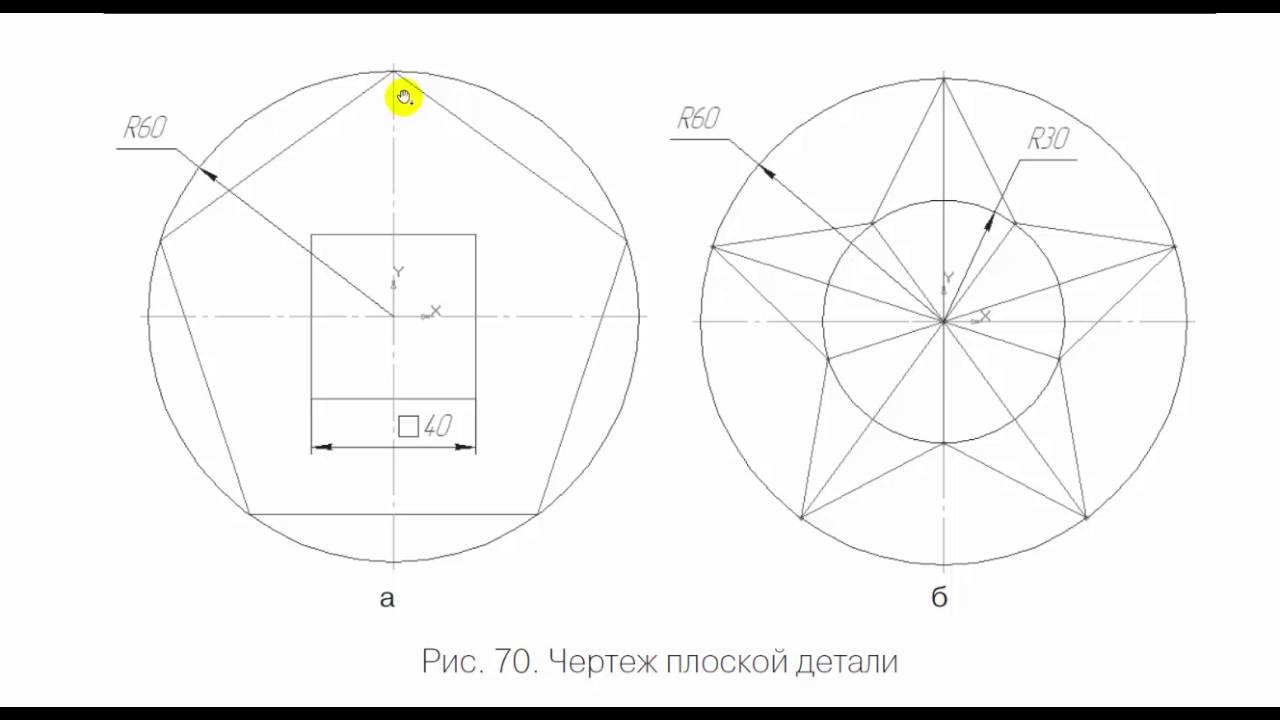
Leave a Comment