Как рисовать геометрические фигуры в объеме: Рисуем объемные тела и фигуры ♥ Рисунки карандашом поэтапно
21.07.2023 
Разное
Как построить призму. Правильное изображение фигуры на рисунке
Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.
В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.
Рисуем четырехгранную призму
Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани.
Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.
Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).
Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.
Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.
Затем нужно найти, где будет находиться переднее вертикальное ребро, и провести линию, на которой отложить высоту тела. После этого намечаются наклоны ребер. Затем прорисовываются все невидимые грани.
Шестигранная призма
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс.
Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.
Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.
Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.
Зачем уметь строить эту геометрическую фигуру?
Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.
С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.
Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.
Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.
В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.
Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.
Похожие записи
Рисование геометрических фигур | Artisthall
Этот урок входит в состав начального комплекса заданий в программе занятий по рисунку. С рисования геометрических фигур начинается знакомство с основными законами и правилами академического рисунка.
Для постановки выбирается одна, две или три геометрические фигуры, например, куб, цилиндр или гипсовая ваза с простым сечением. Предметы изображаются на белой предметной плоскости, на светлом фоне. Акцент делается на изображении фигуры, исключая проработку окружающего пространства. Освещение устанавливается сверху и слева от предметов для наглядного строения классических объемов и большей разницей между светом и тенью, что на первых этапах обучения имеет большое значение для анализа формы и передачи тональных градаций на листе.
Цель рисования геометрических фигур.
- Научиться компоновать предметы на листе;
- Освоить базовые навыки построения и формообразования предметов на плоскости;
- Получить представление о перспективном расположении, сокращении линии горизонта;
- Приобрести навыки работы карандашом, класть штрих по форме, использовать тона и полутона, грамотно передавать расположения планов.
Для работы с последующими заданиями программы, пригодятся все используемые здесь приемы и техники. Главным итогом этого задания, безусловно, является умение располагать предметы в пространстве. Ваш рисунок станет отражением пространства на листе, где все подчинено неизменным законам композиции и расположению светотени на предметах.
Примеры рисунков простых геометрических форм, выполненных учениками нашей школы.
Это основное и важное задание, где на простом примере, без нагромождения предметов и тонов, ясно демонстрируются конструкция и принципы построения ключевой формы, которая лежит в основе большинства вещей — куб.
Работы выполнены нашими учениками.
Научившись правильно строить и изображать углы, грани и плоскости кубика, точно изображать перспективное сокращение, верно определять точки схода, моделировать штрихом объем и тени, вы сможете интуитивно представлять конструкции и объемы любых предметов. Не просто так в основе трехмерного моделирования сложнейших конструкций всегда находиться куб, как база для создания любой последующей формы. А для рисования куб — это воплощение трехмерного изображения; при рисовании его на листе линиями показывается вертикаль как высота, горизонталь как ширина и третья линия как глубина, которая раскрывает пространство, делая предмет объемным.
Сложно переоценить важность этого задания. Пусть не отталкивает простота постановки, так как в ней содержится фундаментальный принцип создания художественных произведений: от простого к сложному.
Подробную информацию о занятиях рисунком вы можете узнать по телефону: 8 903 669-80-89, 8 903 669-49-59.
Смотрите также:
Чертежи площади поверхности и объема
Одним из способов представления трехмерных фигур является ортогональный чертеж , который является причудливым словом для рисования всех сторон трехмерной формы. Это означает, что куб будет выглядеть так:
Это полезно, потому что мы можем определить реальную трехмерную форму, если у нас есть ортогональные чертежи. Но если вы спросите нас, это немного повторяется и не очень интересно. Мы подписались на 3D, и ей-богу, мы собираемся получить 3D.
Наши глаза видят формы в перспективе (3D-очки не обязательны), так что есть лучший способ нарисовать эти формы, чем через угол или перспективные рисунки ?
Было бы излишним говорить вам, что на картинке выше изображен куб. Вы знаете, что это куб. Вы видели его миллион раз в лотке для льда в морозильной камере. Но в этом и смысл: рисовать фигуры такими, какими мы их видим.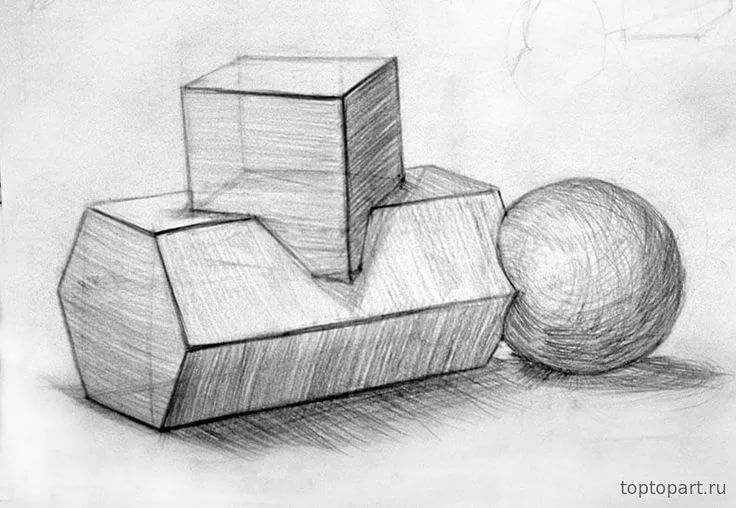
А что, если бы у нас были ортогональные чертежи, и мы хотели бы найти чертеж формы в перспективе? Допустим, у нас есть этот ортогональный рисунок:
Тонкие линии спереди и сверху указывают на некоторые изменения на поверхности, когда мы смотрим на изображение с этих точек зрения. Вид сбоку без изменений. Если мы посмотрим на изображения и соберем их вместе, как Лего, у нас должен получиться перспективный рисунок, который выглядит так:
Немного потренировавшись, вы сможете переводить ортогональные рисунки в перспективные быстрее, чем вы можете сказать. , «преобразование ортогональных чертежей в чертежи в перспективе».
Итак, какие объекты являются трехмерными? Ну много! Все, что существует в реальном мире, имеет трехмерную форму. Как ваш компьютер. И твое глазное яблоко. И Ферби вашей младшей сестры, который, как вы уверены, убьет вас во сне.
Страшно, не так ли?
Но прежде чем мы начнем классифицировать Furbies как что-либо вообще, мы должны начать с основ третьего измерения.
Если у нас есть твердое тело со всеми плоскими поверхностями, которое полностью охватывает область пространства, мы называем его многогранник . «Многогранник» означает «множество», а «-эдр» означает грань.
Отрезки линии пересечения называются ребрами , а точки называются вершинами .
Правильный многогранник имеет все правильные конгруэнтные многоугольники для граней, и все ребра конгруэнтны. Существует всего пять типов правильных многогранников, называемых Платоновыми телами , названными в честь древнегреческого философа Платона, который также изобрел пластину (но не на самом деле).
Призма представляет собой особый тип многогранника с двумя параллельными конгруэнтными гранями, называемыми основаниями . Остальные стороны — параллелограммы. Если призма обычная , это означает, что ее основания — правильные многоугольники.
Пирамида имеет одно основание, а все остальные грани пересекаются в одной вершине. Некоторые пирамиды названы в честь города или цивилизации (Пирамиды Каира, Пирамиды Майя и т. д.), но мы назовем наши пирамиды по их основаниям.
Поскольку основание этой пирамиды квадратное, она квадратная.
Некоторые тела не являются многогранниками. Это фигуры, грани которых не являются плоскими, как многоугольники. Они круглые или изогнутые.
Цилиндр представляет собой пару конгруэнтных круглых оснований на двух различных параллельных плоскостях. Конус — это то, в чем вы едите мороженое, круглое основание с одной вершиной. Сфера — это шар, но ее официальное определение — это набор точек, равноудаленных от заданной точки в трехмерном пространстве. Все они нарисованы ниже.
Эти перспективные рисунки фигур являются их идентификационными значками. Если мы его увидим, мы сможем без проблем его идентифицировать.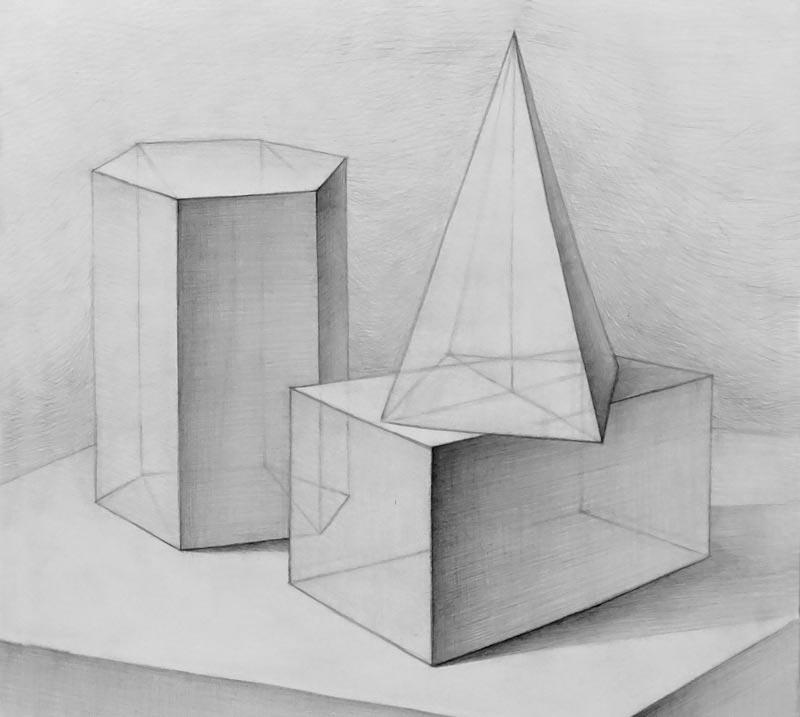
Пример задачи
Как называется фигура? Что такое грани, вершины и ребра?
Гранями являются стороны: ∆ ABC , ∆ ACD , ∆ ADB , и ∆ BCD .
Вершины просто A , B , C и Д .
Ребра представляют собой отрезки AB , AC , AD , BC , BD и CD .
Поскольку все грани представляют собой конгруэнтные равносторонние треугольники, эта форма будет правильным многогранником (одним из пяти Платоновых тел). Поскольку у него всего четыре грани, он называется тетраэдром. («Тетра» означает 4. И вы не понимаете, что такое тетра.)
Говоря о ребрах, гранях и вершинах, есть полезная формула, которая применима к любому многограннику, каким бы безумным он ни выглядел. По словам швейцарца 18-го века по имени Леонард Эйлер, количество граней плюс количество вершин в многограннике равно количеству ребер плюс 2.
Это слишком много, так что вот математическая версия:
F + V = E + 2
Эйлер был человеком, так что этот маленький трюк называется Формула Эйлера .
Если вы все еще не понимаете трехмерные фигуры, посмотрите наше видео, которое поможет вам:
Онлайн-калькулятор: Объем геометрических фигур
Исследование Математика
Вычисляет объем геометрических фигур : куб, призма, пирамида, усеченный конус, цилиндр, сфера, эллипсоид.
Эта статья содержит сборник калькуляторов для расчета объема геометрических фигур. Первоисточник расчетных формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Сторона (H)
Длина стороны
Точность расчета 9000 5
Знаки после запятой: 5
Объем
Объем прямоугольной призмы
Размеры прямоугольной призмы
Формула:
Объем прямоугольной призмы
Ширина (Ш)
Высота (H)
Длина (L)
Точность расчета
цифры после десятичной точки: 5
Том
Обрать объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания (Sb)
Площадь основания пирамиды.
Leave a Comment