Как правильно начертить куб: Страница не найдена – Spanishlove

---

08.08.1971 Разное

---

как нарисовать куб с любого ракурса — Gamedev на DTF

Советуем приготовить планшет или лист бумаги и ручку, чтобы все сразу попробовать. Читать эту статью просто так не имеет смысла — тут все про практику.

31 198 просмотров

Зачем художнику уметь рисовать куб с любого ракурса?

Освоив кубы, вы сможете рисовать любые объекты: машин, людей, архитектуру. Тоже с любого ракурса, быстро и понятно. Например, вот так можно свести к кубам фигуру человека:

Известный художник Скотт Робертсон рисует технику, отталкиваясь от геометрических примитивов.

Этому методу следует и Moderndayjames:

Дальше будет много примеров. Советуем попробовать нарисовать основные моменты, чтобы лучше понять, о чем речь. Получится своеобразный конспект.

Статья написана по материалам ресурса How to sketch.

Что такое перспектива?

Рисовать куб с любого ракурса — это рисовать его в перспективе.

Представьте камеру — она заменит нам наблюдателя. На расстоянии от камеры стоит куб. Между камерой и кубом находится стекло.

Расположение объектов.

Стекло здесь — так называемая картинная плоскость. Проведем от камеры сквозь стекло линию — получится то, что называется лучом зрения (ЛЗ). Луч зрения всегда перпендикулярен картинной плоскости. Эти обозначения понадобятся нам дальше.

Нам нужно знать, как линии нашего объекта расположены в пространстве относительно чего-либо. Положение камеры — наша путеводная звезда. Рисовать в перспективе — значит представлять изображение с определенной точки зрения. Не бывает изображения без зрителя.

Дальше мы будем рассматривать сцену с двух точек зрения: то, как ее видит камера, и то, как она расположена относительно объекта. Это нужно, чтобы проще ориентироваться в пространстве.

Куб начинается с квадрата

Куб состоит из шести квадратных плоскостей, соединенных вместе.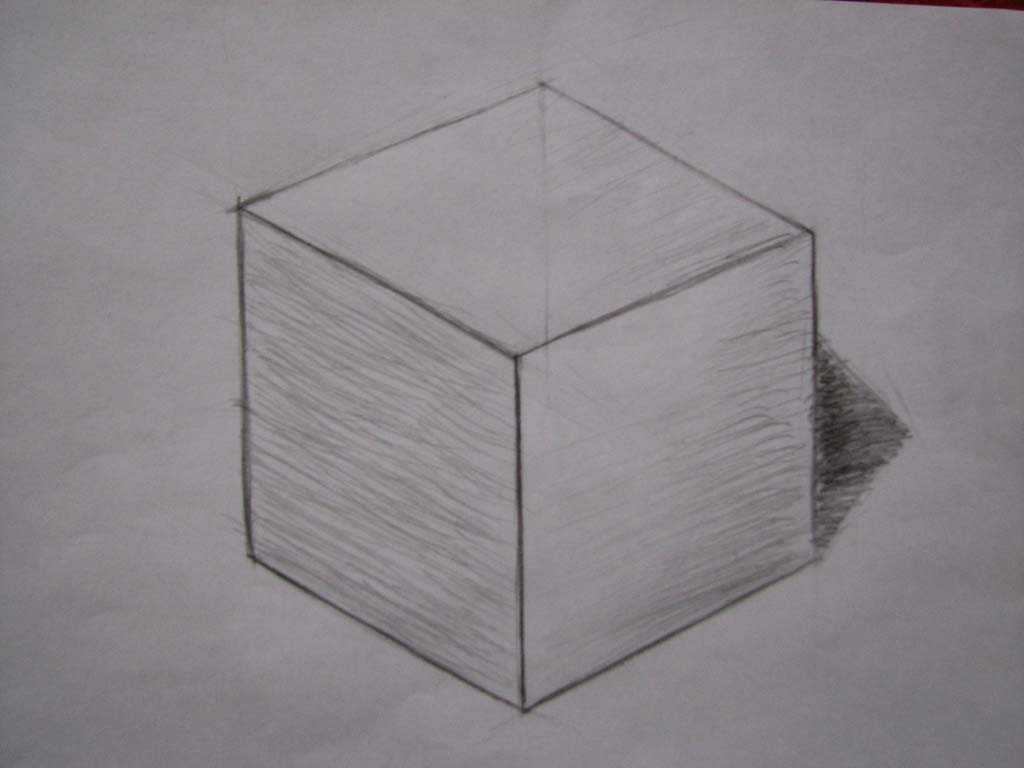

Чтобы нарисовать куб, нам нужно знать, как правильно расположить в пространстве квадрат во всех без исключения случаях и с любого возможного ракурса.

Шесть квадратных плоскостей в пространстве.

Здесь мы добавим в наш словарь новое слово — нормальная линия или просто нормаль. Нормаль — это линия, перпендикулярная какой-либо поверхности. Если вы поставите карандаш вертикально на стол, он будет совпадать с направлением нормальной линии. Вы можете встретить этот термин в 3D, но в 2D его тоже используют.

У каждой плоскости есть бесконечное количество этих нормальных линий. Для простоты мы нарисуем только одну по центру.

Возьмем квадрат и расположим его перед камерой. Если нормаль перпендикулярна картинной плоскости и тем самым совпадает с лучом зрения, значит, мы видим поверхность без каких-либо искажений. В данном случае — обычный квадрат.

Слева — расположение объектов, справа — что видит камера.

Если мы наклоним нашу фигуру в каком-либо направлении, то нормаль больше не будет смотреть прямо на картинную плоскость. Поверхность прямоугольника сожмётся в том направлении, куда смотрит нормаль. Этот принцип называется сжатие по нормали. Каждая плоскость всегда сжимается только по своей нормальной линии.

Слева — расположение объектов, по центру — что видит камера, справа — реальный размер плоскости.

На приведенном примере боковые стороны прямоугольника сужаются кверху (с точки зрения камеры). Так получается потому, что это параллельные линии, которые уходят вдаль (относительно картинной плоскости). А вот линии, параллельные картинной плоскости, никогда не сходятся.

Слева — расположение объектов, справа — что видит камера.

Что такое линия горизонта?

Параллельные линии, которые уходят вдаль, сходятся на линии горизонта. Эта истина так широко известна и непреложна, что авторы никогда не пересматривают ее обоснование. А мы пересмотрим — чтобы лучше понять, о чем речь.

Наша камера стоит строго вертикально, то есть ее нижняя плоскость параллельна плоскости земли. Представим себе не один, а несколько горизонтальных прямоугольников перед камерой. По мере того, как эти плоскости всё выше поднимаются над землёй, они всё сильнее сжимаются. В какой-то момент плоскость визуально сожмется в плоскую линию — это будет линия горизонта.

Слева — расположение объектов, справа — что видит камера.

Находим линию горизонта.

Слева — расположение объектов, справа — что видит камера.

Параллельные линии, расположенные на горизонтальных плоскостях (на любой из них) сходятся на линии горизонта. Точки, в которых они сходятся, называются точками схода (ТС).

Слева — расположение объектов, справа — что видит камера.

Как видите, у каждого набора параллельных линий есть своя собственная точка схода. Для перспективы типично наличие центральной (ЦТС), левой (ЛТС) и правой (ПТС) точек схода.

Ориентируемся в пространстве

Теперь попробуем разобраться в том, как прямоугольники изменяются по мере увеличения расстояния от зрителя.

Возьмем несколько прямоугольников и выстроим их в ряд. Все они имеют одинаковый размер и расположены впритык друг к другу. И хотя в действительности все они имеют одинаковый физический размер, каждый последующий прямоугольник в перспективе становится меньше. Благодаря этому явлению параллельные линии

«сходятся на линии горизонта».

Прямоугольники в пространстве.

Благодаря изменению размера наш мозг воспринимает глубину. Но оно происходит не линейно: каждый прямоугольник сжимается по своей нормали, когда его наклоняют относительно зрителя. Плоскость сжимается тем сильнее, чем она ближе к линии горизонта.

Разница в размере между парами прямоугольников, лежащих ближе к зрителю, ярче выражена, чем между теми, которые ближе к горизонту.

Измеряем глубину

Проведём три горизонтальные линии в перспективе аналогично прямоугольникам выше. Изменяем только одно требование: интервалы между ними должны быть одинаковыми. Что мы увидим? Отрезок B в два раза короче, чем A, но C в шесть раз короче, чем B.

Каждый следующий сантиметр на бумаге вмещает в себя все больше и больше пространства по мере приближения к горизонту.

Это важно понимать при рисовании не только механизмов, но и природных форм. Даже фигуры человека. Как и любой другой объект, тело существует в пространстве. Важно точно знать, где именно расположены ключевые точки тела. А для этого нужно освоить измерения в перспективе. Набравшись опыта, вы сможете делать обоснованные догадки, уже не рисуя вспомогательные конструкции.

Для правильного куба придется узнать кое-что об эллипсах

Теперь нам нужно нарисовать эллипсы. Тут нам пригодятся те же знания, что мы получили, изучая квадратные плоскости: потому, что плоскость может быть любой формы, в том числе овальной или круглой.

У плоского круга или овала тоже есть нормальная линия, и она точно так же перпендикулярна поверхности плоскости.

Нормальная линия плоского эллипса всегда совпадает по направлению с его малой осью.

Принцип тот же, что и в случае с прямоугольниками. Слева — вид сверху, справа — что видит камера.

Важно помнить, что у круга всегда одинаковый диаметр, в каком бы направлении мы его не провели. После сжатия круг превращается в овал, и у него появляется самый длинный (большая ось эллипса) и самый короткий (малая ось эллипса) диаметры.

Большая ось не меняет свою длину, как бы сильно мы ни наклоняли плоскость. Малая ось перпендикулярна большой, а ее направление совпадает с нормальной линией. Длина малой оси меняется сильнее всего, когда мы наклоняем плоскость по отношению к камере.

Большая ось сейчас расположена горизонтально, а малая — вертикально. По ней и происходит сжатие. Размеры большой оси не меняются.

Зачем в тексте про кубы информация про эллипсы?

Эллипсы помогают определить направление нормальной линии поверхности, поэтому их удобно использовать, даже если на рисунке нет видимых круглых плоскостей. Они подсказывают, в каком направлении сжимать плоскость, когда она наклонена по отношению к зрителю.

Слева плоскость расположена прямо относительно камеры, справа — наклонена относительно камеры.

Еще эллипс может пригодится, чтобы определить угол наклона плоскости относительно зрителя. Сильнее наклон, сильнее сжатие.

Нет наклона = нет сжатия. В центре и справа плоскости наклонены относительно зрителя.

И, последний, самый важный пункт. Эллипс

помогает найти пропорции идеального квадрата: круг, вписанный в квадрат, касается каждой из четырех сторон точно посередине.

Круг всегда касается сторон квадрата посередине.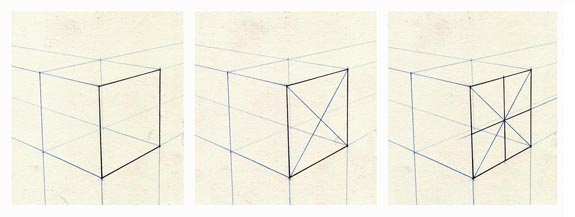

Первый угол — 90 градусов

Помимо пропорций квадрата, нам нужно убедиться, что у нашей фигуры есть четыре прямых угла (по 90 градусов). Для этого необходимо правильно построить хотя бы один угол — три остальных встанут на свои места.

Эллипс поможет найти правильный угол между двумя линиями на одной плоскости.

Исходное расположение объектов. Смотрите ниже, как мы превращаем круг в квадрат.

Определяем пропорции квадрата с заданного ракурса, используя эллипс.

Слева — что видит камера, справа — расположение камеры относительно фигуры, вид сверху.

Проведем нормальную линию (она здесь вертикальная, потому что плоскость горизонтальная). Её можно проводить в разных местах — в зависимости от того, как мы хотим развернуть к себе угол будущего квадрата.

Как далеко нормаль должна выходить за пределы эллипса до той точки, где она пересекается с касательными? Это зависит от угла наклона эллипса.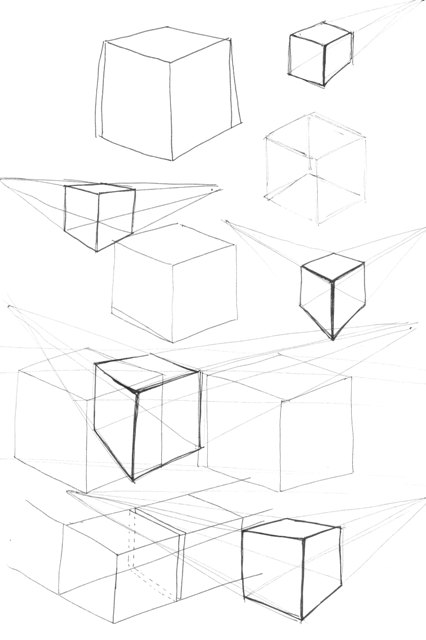

Вид из камеры. Нормаль выходит из центра эллипса. Чем меньше его наклон по отношению к камере, тем длиннее линия.

Чем ближе линия горизонта к эллипсу (с учётом его размера), тем сильнее перспективное искажение, и тем быстрее сходятся линии. Это также значит, что объект или находится близко к зрителю, или он большой. Изображение выглядит так, как будто снято через широкоугольный объектив.

Если линия горизонта находится далеко от эллипса, перспективное искажение будет слабым. Линии будут сходиться медленно, объект покажется маленьким или будет расположен далеко от зрителя. Это эффект длиннофокусного объектива.

Слева горизонт очень близко и линии сходятся быстрее, справа горизонт далеко и линии сходятся медленнее.

Здесь видно, что вертикальная линия в обоих случаях выходит за пределы эллипса на одно и то же расстояние. Нижний угол квадрата одинаковый. Разница только в силе перспективы. И ещё раз напоминаем: линия горизонта перпендикулярна нормали эллипса (малой оси).

Горизонт — это по сути ещё одна плоскость, параллельная нашему эллипсу. Просто она полностью наклонена по отношению к зрителю.

Итак, наш эллипс готов.

Превращаем эллипс в куб

У куба шесть граней, но одновременно мы можем увидеть лишь три из них. Так что, простоты ради, мы сосредоточимся только на видимых сторонах (пока). Начнем с верхней грани. Вы уже знаете, как изобразить горизонтальный квадрат в любом возможном положении, так что сделайте это — нарисуйте квадрат вокруг эллипса.

Теперь нужно дорисовать две боковые грани. Чтобы найти их, используйте вертикально расположенные рёбра куба — нормали к верхней плоскости.

Осталось еще узнать длину вертикального ребра. Оно параллельно картинной плоскости и становится длиннее, когда перемещается ближе к нам в пространстве (как и любой другой объект), в соответствии с конвергенцией (сближением) линий.

Мы предполагаем, что ребро немного длиннее, чем большая ось нашего верхнего эллипса, на которую тоже не действует перспективное сокращение.

Есть одна хитрость, которая помогает проверить, правильно ли мы построили боковые грани. Это можно сделать с помощью эллипса. Нарисуйте эллипс, малая ось которого направлена в правую точку схода. Эллипс должен касаться рёбер куба посередине. Затем просто закройте снизу левую грань с помощью линии, идущей к левой точке схода. А потом правую грань — линией, идущей к правой точке схода:

Наш куб готов:

Как клонировать наши кубы

Для этого вернемся к рисованию прямоугольников. У каждого прямоугольника есть диагонали, они пересекаются в его центре. Диагонали помогают нам рисовать одинаковые прямоугольники.

Диагонали прямоугольника пересекаются в его центре.

Давайте потренируемся. Найдите центр прямоугольника, используя диагонали.

• Нарисуйте среднюю линию прямоугольника и продолжите ее в том направлении, куда собираетесь клонировать прямоугольник. Средняя линия пересечёт сторону прямоугольника в точке А.

• Продолжите стороны прямоугольника в том же направлении.

Найдите центр прямоугольника. Продлите линии в ту сторону, куда будете его клонировать.

• Проведите через точку A линию из дальнего угла прямоугольника. Она пересечет его продлённую сторону в точке B. Точка B отмеряет ширину нового, точно такого же прямоугольника.

• Теперь проведите вертикальную линию. Она станет дальней стороной нового прямоугольника.

Удвоение прямоугольника

Вы можете удваивать прямоугольники с помощью диагонали не только на плоскости, но и в перспективе. Сначала найдите центр прямоугольника, затем размножьте его во всех направлениях. Заполните всю страницу такими конструкциями.

Клонирование прямоугольника во всех направлениях.

Следует помнить, что в перспективе центр прямоугольника смещается по отношению к зрителю. Это происходит из-за схождения линий. Когда перспективное искажение небольшое (горизонт далеко по сравнению с размерами объектов), линии сходятся медленно, и центр прямоугольника смещается незначительно. И наоборот, смещение центра очень ярко выражено в случае сильного перспективного искажения.

Смещение центра.

Время активной практики. Клонируем кубы.

Постройте куб. Нижняя грань параллельна земле, никаких причудливых наклонов. Затем клонируйте любую грань куба с помощью метода диагоналей. Наметьте линии, которые будут направлены в точки схода.

Нарисуйте куб в перспективе.

Помните, квадраты сжимаются сильнее по мере удаления от зрителя. Если сравнивать первый и второй квадраты, этот эффект выражен ярко. Для каждого последующего квадрата он менее очевиден, но присутствует всегда.

Постройте новые кубы, клонируя квадратные плоскости.

Нарисуйте кубы один за другим. Заполните ими всю страницу.

Рисуйте «насквозь»

Сквозное построение означает, что вы рисуете твердые тела так, будто они прозрачные. Так вы всегда будете знать, где именно в пространстве находятся те участки поверхности тела, которые недоступны глазу. Это поможет правильно располагать тела по отношению друг к другу.

Переходим к практике:

Рисуем куб «насквозь», со всеми с невидимыми гранями.

Клонируем куб в сторону ПТС. Не забываем оставить между ними пространство величиной с такой же куб.

Повторяем упражнение к ЛТС.

Интересная деталь. Как вы могли заметить, уходя вдаль, некоторые плоскости сильнее сжимаются (мы уже знаем почему), а другие — наоборот, больше открываются зрителю.

Это происходит потому, что угол между лучом зрения и поверхностью этих плоскостей приближается к прямому (90 градусов).

Как нарисовать куб с любого ракурса за пять шагов?

Теперь переходим к самому интересному!

Шаг 1. Нарисуйте эллипс. Он может располагаться на любой грани куба. Здесь вас должны волновать только сжатие и направление нормали.

Шаг 2. Проведите нормальную линию исходя из того, как вы хотите развернуть ближайшее к зрителю ребро куба. Линия горизонта для этого куба фактически не будет горизонтальной. Да, получился немного каламбур.

Какой она тогда должна быть? Просто перпендикулярной нормали нашей плоскости. Это единственное требование.

Шаг 3. Определитесь с силой перспективного искажения. В нашем случае линия горизонта находится за пределами холста, поэтому оно выражено слабо.

Шаг 4. Определите правильную длину «вертикального» ребра куба, используя эллипс или просто на глаз. Проведите линию к правой точке схода, чтобы закрыть грань снизу.

Шаг 5. Последняя грань сама станет на место. Просто постройте правильные параллельные линии к тем, которые уже есть.

Еще один способ: построение с помощью масс

Масса — это простое сферическое или колбасоподобное тело, используемое в качестве основы для построения сложных форм. Думайте о ней как о комке глины, существующем в трехмерном пространстве.

Это не плоская фигура на бумаге, у нее есть реальный физический объем.

Используя массы, легче воссоздать чувство размера в рисунке. Они же помогут решить проблемы перспективного искажения и наложения объектов друг на друга. Как видите, метод масс работает со всеми тремя ключевыми компонентами глубины в вашем рисунке.

Давайте теперь создадим куб из сферической массы. Независимо от того, как он развернут, куб идеально вписывается в сферу.

Куб, вписанный в сферу.

• Нарисуйте круг.

• Постройте куб, используя знания, усвоенные из предыдущих блоков. Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.

• Прямо сейчас нарисуйте целую страницу кубов, вписанных в сферы. Меняйте размер и ракурс.

Основная идея: каждая масса имеет центр. Центр сферической (или яйцеобразной) массы всегда совпадает с ее геометрическим центром. Давайте построим несколько одинаковых по размеру масс с равными промежутками между ними.

Постройте квадраты в перспективе.

• Нарисуйте сферу вокруг каждой точки. Контур каждой сферы должен касаться линий, которые направлены в центральную точку схода, — если вы хотите, чтобы сферы были одинакового размера.

Нарисуйте сферическую массу вокруг обозначенной точки.

• Встройте кубы внутрь сферических масс. Разворачивайте их, как хотите, они всё равно будут одного размера, и расстояния между их центрами будут одинаковыми.

Нарисуйте куб внутри каждой сферы.

Поднимем кубы над землей

• Нарисуйте на земле квадрат, затем проведите внутри него прямую линию. Эта линия представляет собой расстояние между двумя кубами. Обозначьте точку схода, в которую направлена линия.

Проведите прямую линию внутри квадрата.

Постройте вертикальную плоскость.

Нарисуйте массы одинакового размера с центрами в верхних углах плоскости.

Впишите куб в каждую массу.

Рисуем кубы в пространстве по произвольной траектории

Для начала вспомним про диагонали и построим с помощью них кривую в перспективе. Вот, как это сделать.

Шаг 1. Кривая в ортогональном виде, то есть без перспективных искажений, прямо перед зрителем.

Шаг 2 выглядит так. Помните, чем ближе линия горизонта к эллипсу, тем сильнее перспективное искажение.

• Нарисуйте квадрат в одноточечной перспективе, где линии параллельны либо картинной плоскости (тогда они вообще не сходятся), либо лучу зрения. Те, которые параллельны лучу зрения, сходятся в центре линии горизонта. Эта точка называется центральной точкой схода, как вы, возможно, помните. Это самый простой способ нарисовать прямоугольник.

Шаг 3. Постройте квадрат вокруг вашего круга. 

• Затем проведите диагонали и средние линии. Они будут служить вашим ориентиром.

• Перенесите точки пересечения кривой с этими линиями из вашего ортографического рисунка. Например, если кривая касается верхней стороны квадрата по центру, она будет делать то же самое и в перспективе.

Шаг 4. Перенесите кривую из вида сверху в перспективный вид, опираясь на опорные точки.

Объединяем два упражнения

Наша цель — построить кубы одинакового размера с одинаковым расстоянием между ними, но расположенные на неправильной траектории.

Шаг 1. Постройте кривую в перспективе.

• Отметьте на кривой точки, соблюдая равные интервалы между ними. Каждая точка соответствует центру массы. Определите размеры масс, которые находятся далеко от зрителя. Тогда вам будет легче определить на глаз размеры масс, расположенных в промежутках.

• Вот как это можно сделать: проведите прямую, проходящую через две точки, и продолжайте её, пока она не пересечётся с горизонтом в точке схода. Линии, по которым мы будем выравнивать размер масс (они касаются контуров обеих сфер), тоже должны быть направлены в эту точку схода.
  

Шаг 2. Отметьте на теле кривой точки с равными интервалами.

Шаг 3. Нарисуйте массы одинакового размера. Точки на кривой — это их центры.

Впишите куб в каждую массу.

А теперь пора нарисовать пару десятков кубов!

С разных ракурсов, в разных местах, с перекрытиями. Попробуйте разную силу перспективного искажения. Обязательно нарисуйте, даже если считаете, что все поняли. Это ОЧЕНЬ поможет рисовать потом любые другие предметы. Верьте в практику!

Что можно сделать:

Пример домашнего задания.

Дополнительные материалы

Здесь можно посмотреть еще видео по теме.

Когда разберетесь с этими упражнениями, можно попробовать порисовать технику, как в этом плейлисте ModernDayJames. Стартовать можно отсюда:

А тут рассказывают, как понимание геометрических примитивов поможет в рисовании динамичных поз:

Текст переведен авторами Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.

Вы не знаете, как будет правильно нарисовать куб? Эта статья для вас!

Рассматривая экспозицию в музее и любуясь произведениями искусства, мы не задумываемся над тем, что эти великие мастера прошли долгий путь от самых элементарных азов. В любой художественной школе или студии одним из первых будет урок по изображению куба. Да, именно с этой элементарной фигуры начинается настоящий путь в искусство. В этом уроке мы вам расскажем, как нарисовать куб.  

Что нужно приготовить для работы

1. Плотную бумагу для рисунка.
2. Простые карандаши разной твердости. Все они должны быть хорошо заточены и иметь острый грифель.
3. Ластик.
4. Куб. Для этих целей можно использовать небольшую коробку, предварительно оклеив ее белой бумагой. Как вариант — можно сделать куб самим.
5. Настольная лампа или другой источник освещения, который вы сможете направлять на вашу модель. Можно обойтись и без лампы, но в этом случае тени у вас будут сильно рассеяны, не будет четких граней у куба.

Шаг 1

Постановка композиции. Возможно, звучит громко, но без этого вам будет сложно понять, с чего начинать работу над рисунком. Возьмите белый лист бумаги, положите его на стол или на стул, как вам будет удобно. На лист бумаги поставьте куб и направьте на него луч света от лампы. Таким образом ваша композиция из куба получит хороший объем. У вас будет четко выраженная светлая сторона, лицевая сторона (будет смотреть на вас) и темная сторона куба. Помимо этого, будет еще тень, которую отбрасывает куб. Итак, как нарисовать куб карандашом?

Шаг 2

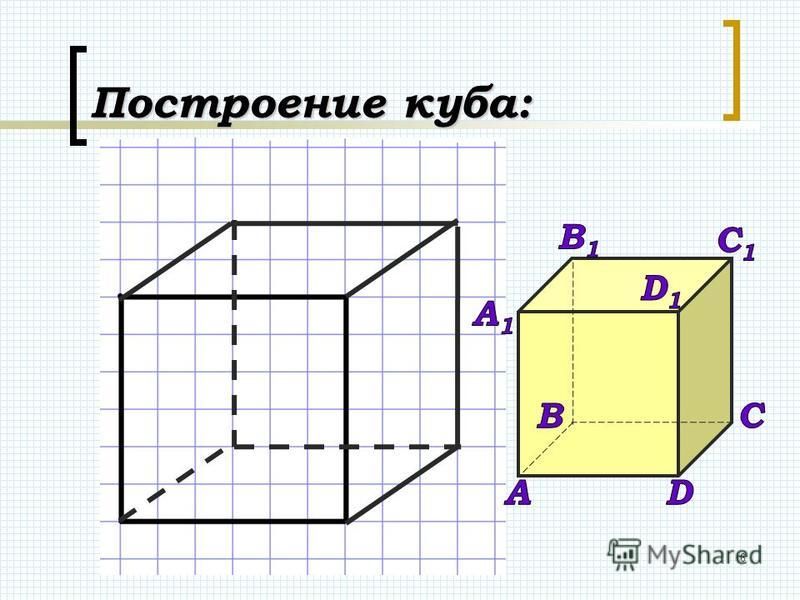
На первой схеме вы увидите разные варианты того, как нарисовать куб. Посмотрите внимательно и определите, где у вас будет линия горизонта, именно к ней и будут сходиться боковые грани вашего куба. Если на глаз тяжело проводить линии,  воспользуйтесь линейкой. Возьмите карандаш средней твердости или твердый и нарисуйте одну плоскость куба. Начните с самого простого варианта. Поставьте куб так, чтобы его одна плоскость была расположена параллельно вам. Грубо говоря, вы перед собой в этой позиции будете видеть квадрат, который и надо будет нарисовать на бумаге.

Шаг 3

Теперь в том, как нарисовать куб, вам будет помогать перспектива. Немного выше вашего квадрата поставьте точку. Теперь от верхних углов куба проведите линии к этой точке. Видите, у вас что-то получается. Вам останется только определиться с шириной верхней стороны куба (крышки) и провести вертикальную линию.

Шаг 4

Как поэтапно нарисовать куб? Потренируйтесь, усложните задачу — сдвиньте куб гранью к себе и, посматривая на первую схему, определите, где у вас будет горизонт. Проведите к нему линии от углов куба. Закройте боковые стороны и верх куба. Такой рисунок наверняка вам уже больше понравится.

Шаг 5

Уберите ластиком ненужные линии и берите в руки мягкие карандаши. Теперь пришло время создавать объем. Самую светлую сторону (в нашем случае это верх куба) не трогайте. У вас остается две стороны. Одну заштрихуйте, нажимая на карандаш легко. Другую, которая в тени, заштрихуйте интенсивнее, если нужно — пройдитесь еще раз. Не забудьте и тень от куба, она должна быть еще интенсивнее, а также иметь растяжку от самого темного места под кубом, и чем дальше от предмета, тем светлее.

Теперь вы знаете, как рисовать куб, и вам остается только оттачивать свое умение видеть все полутона и воспроизводить их на бумаге. Тренируйтесь: поворачивайте куб, изменяйте луч света — и со временем у вас все получится.

Простое руководство по рисованию кубиков и страница-раскраска кубиков

2-й класс | 3 класс | 4 класс | 5 класс | Мелки | Рисование | Легкие уроки рисования | Элементы искусства | Разное

13 июля 2021 г. 6 октября 2022 г.

Ниже вы найдете простое пошаговое руководство по рисованию куба и страницы-раскраски куба. Этот не требует стирания, что отлично подходит для тех, кто только начинает.

• Переход к кубу, учебник

• Страница раскраски куба

Некоторые руководства по рисованию куба, которые вы можете найти в Интернете, включают в себя рисование передней и задней сторон, а затем их соединение. Однако это требует более объемного мышления, поэтому мне нравится эта версия простого рисования передней части, затем боковых сторон, а затем соединения концов. Нет необходимости ничего стирать, и, возможно, это немного легче понять.

Куб    – это твердая трехмерная фигура с 6 квадратными гранями. Многие ученики учатся делать шаблон для урока математики или геометрии, вырезая шаблон в форме креста и складывая его вместе, чтобы понять, как он сочетается.

Используйте кнопку ниже, чтобы загрузить PDF-учебник

Open Cube PDF-учебник

Cube Coloring Page

open Cube Coloring page

Материалы для рисования куба

Бумага для рисования
• 90 Это хорошие вещи, которые можно купить оптом по хорошей цене.
• Карандаши. Не тратьте деньги на самый дешевый бренд. Это делает красивые темные линии.
• Черный маркер. Перманентный маркер даст вам приятный темно-черный цвет.
• Мелки . Пакеты с широким диапазоном цветов являются наиболее полезными.
• Примечание. Все вышеперечисленное является партнерскими ссылками Amazon.

Инструкции по рисованию куба для детей

Необходимое время: 30 минут.

Как нарисовать куб

1. Начните с рисования буквы L, как показано на рисунке.

2. Добавьте вертикальную линию.

3. Соедините вверху, чтобы завершить квадрат.

4. Нарисуйте первую боковую линию.

5. Добавьте вторую боковую линию.

6. Проведите третью боковую линию.

7. Соедините концы с правой стороны.

8. Соедините концы сверху.

9. Обведите маркером и цветом. Затенение поможет вашему кубу выглядеть еще более трехмерным.

Сохраните меня на своей доске Pinterest!

Больше увлекательных графических проектов

• Перспектива для начинающих
• Комната в перспективе
• Буквы в 3D
• Числа в 3D
• Здания в 3D

Похожие сообщения

Как нарисовать куб с помощью четырех простых приемов

Научиться рисовать куб можно с помощью нескольких простых приемов. В этом базовом уроке я покажу вам четыре техники, которые можно использовать для достижения вашей цели. Во-первых, у вас будет возможность нарисовать сплошной куб, используя всего два квадрата и несколько линий. Это самая простая техника, которую вы можете найти, чтобы создать эту форму.

Далее вам будут доступны еще три урока, которые помогут вам нарисовать куб с использованием перспективы. Эти формы можно сделать с помощью одной точки схода, двух точек схода и трех точек схода. Нарисовать фигуру в перспективе может быть немного сложнее, но я уверен, что вы справитесь с задачей, используя приведенные ниже простые советы. Готовый? Давайте начнем эту серию прямо сейчас! 🙂

Как нарисовать куб из двух квадратов

Сначала давайте нарисуем простой мультяшный куб из двух идеальных квадратов. Для этого первого шага нарисуйте квадрат на левой стороне листа бумаги. Нам нужно немного места справа, чтобы правильно нарисовать фигуру.

Затем нарисуйте вторую фигуру позади первой. Как вы можете видеть ниже, новая форма немного выше, а также справа от исходной формы. Часть, расположенная внутри исходного квадрата, должна быть скрыта.

Пришло время добавить немного глубины, создав три основные линии.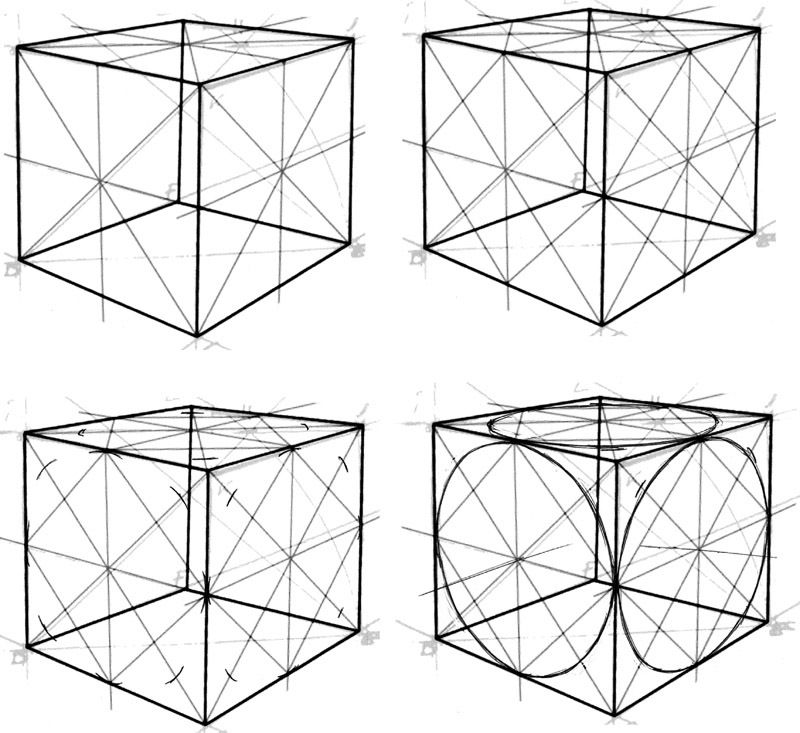 Верхние углы создаются путем соединения вершин вместе с этими новыми линиями. Вы можете увидеть новые дополнения ниже (выделены красным).

Теперь, когда все линии нарисованы, вы можете стереть линии, видимые внутри куба. Линии, которые необходимо удалить, показаны ниже (выделены серым цветом). Хорошо сделано! Мы создали наш первый мультипликационный куб!

Конечно, вы можете изменить угол фигуры, нарисовав дополнительные линии под квадратами, а не сверху. Ниже вы можете увидеть, как такая модификация может создать нечто совершенно иное.

рисование куба с использованием одноточечной перспективы

Хорошая работа: научиться рисовать куб, используя только два основных квадрата. Эту первую технику очень легко воспроизвести. Теперь мы приступаем к самой сложной части этой серии: созданию перспективы с использованием точек схода.

Наш первый пример состоит из единственной точки схода. Начните с наброска квадрата в нижней части иллюстрации. В верхней части изображения (слева) вы можете нарисовать точку схода (обозначена зеленым цветом ниже).

Затем выберите все три вершины квадрата и нарисуйте длинные прямые линии, как показано ниже. Поскольку мы хотим нарисовать куб, нам нужно нарисовать еще две линии, чтобы достичь нашей цели.

Эти две линии помогут нам закрыть фигуру и завершить наш мультяшный куб. Для этого шага вам нужно нарисовать одну вертикальную линию сбоку и горизонтальную сверху. Обе линии соединяются, чтобы создать еще один угол.

Проведение этих линий ближе к точке схода также может создать забавную форму. Однако, поскольку наша цель — создать куб, предыдущая версия была более подходящей.

Это результат удаления точки схода и корректировки всех линий.

Рисование куба с использованием двухточечной перспективы

Следующий пример изображает куб, состоящий из двух точек схода. Сначала нарисуйте обе точки с обеих сторон изображения (в верхней части этого). Посередине иллюстрации (и ближе к низу) нарисуйте короткую вертикальную линию.

Когда вы закончите создание этой линии, добавьте еще четыре прямые, чтобы соединить исходную линию с точками схода. Большой! Это упражнение по рисованию куба идет хорошо! 🙂

Теперь нарисуйте две короткие вертикальные линии, чтобы создать обе стороны фигуры. Вы можете увидеть эти новые дополнения ниже (также окрашены в красный цвет). Еще один шаг, и мы закончили с этим вариантом.

Вы можете завершить этот урок о том, как нарисовать куб, используя две точки схода, нарисовав еще две линии. Эти линии соединяют оба верхних угла с точками схода.

После того, как все линии будут укорочены, а обе точки схода стерты, у вас должна получиться фигура, похожая на ту, что показана ниже.

Рисование куба с использованием трехточечной перспективы

Пока это наша самая большая задача. В этом последнем уроке из этой серии о том, как рисовать куб, я покажу вам, как использовать три точки схода. Начните с рисования красной точки посередине. Вокруг этой точки нарисуйте все три точки схода, как показано ниже.

Затем соедините красную точку со всеми тремя точками схода прямыми линиями.