Как нарисовать куб 3 д: Как нарисовать куб — YouLoveIt.ru
16.05.2023 


 Разное
Разное
Объемный куб по клеточкам — 97 фото
Рисунки по клеточкам в тетради
Объёмные фигуры по клеточкам в тетради
Рисунки по клеточкам в тетради
Р̊б̊ъ̊е̊м̊н̊ы̊ у̊р̊е̊с̊т̊
Объемный крест по клеточкам
Рисование в клеточку в тетради
Узоры по клеточкам в тетра
3д рисунки карандашом на бумаге в клетку
Сложные геометрические фигуры по клеточкам
Объёмные фигуры по клеточкам в тетради
Сложные орнаменты по клеточкам
Объемные фигуры на бумаге
Объемные фигуры на клетках
Рисование по клеточкам 3д
Иллюзия в клетку
Узоры для рисования по клеткам
Рисунки по клеточкам в тетради
Узоры по клеточкам сложные
Узоры по клеточкам в тетради
Геометрические фигуры по клеточкам
Объемный крест
Объемные рисунки по клеткам
Фигуры в клетку
Рисование геометрических фигур по клеточкам
Рисование в тетради в клетку
Объемные фигуры по клеткам
Копирование геометрических фигур
Треугольник Эшера
Фигуры Эшера и Пенроуза
Узоры в тетради в клетку
Объемные рисунки по клеткам
Кубик Рубика карандашом
Кубики + раскраски
Узоры в тетрадке в клеточку
Узоры по клеточкам в тетради
Геометрические узоры в тетради
Куб по клеточкам
Геометрические раскраски
Узоры по клеточкам
3d фигуры
Раскраска объемный кубик Рубика
Геометрический орнамент клетка
Интересные фигуры
Узоры на тетрадку в клетку
Оптическая иллюзия кубик Рубика
Кубик рубик объемный
Узоры по клеточкам в тетради
Рисунки по клеточкам карандашом
Лёгкие геометрические фигуры
Объемные фигуры на клетчатой бумаге
3d квадрат по клеточкам
Геометрические мандалы по клеточкам
Треугольник Пенроуза Эшер
Кубик для рисования
Сложные геометрические фигуры
Фигуры на бумаге в клетку
Невозможные узоры
Фигуры в клетку
Треугольник Пенроуза Эшер
Рисования маркером по клеточкам
Оптическая иллюзия куб
Объемный крест по клеточкам
Треугольник Пенроуза Эшер
Сложные геометрические фигуры 3д
Рисунки GJ rktnjxmrfvb карандашом
Рисунки по клеточкам в тетради
Рисование по клеточкам для детей
Фигуры в клетку
Узоры по клеточкам в тетради
Разрежьте фигуру на три
Рисунки по клеточкам в тетради маленькие
Рисование по клеточкам простым карандашом
Эшер орнамент геометрический
Клеточные узоры в тетради
Портал по клеточкам
Логотипы по пикселям
Узоры в тетради в клетку
Повтотори по клеточкам
Рисунки на листике в клеточку
Рисование по клеточкам в тетради для детей
Значки по клеточкам в тетради
Рисование по клеткам
Узоры по клеточкам в тетради
Фигурки по клеткам
Геометрические оптические иллюзии
Куб на листке в клетку
Узоры по клеточкам
Маленькие 3д рисунки по клеточкам
Узоры по клеточкам в тетради
Рисунки по клеточкам 8bit
Многогранники Эшера
Сердечко по клеточкам в тетради
Сложные орнаменты по клеточкам
Рисование по кубикам в тетради
Рисунки по клеточкам в тетради
Комментарии (0)
Написать
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Как нарисовать невозможный 3д куб Эшера поэтапно – Рисуем невероятные фигуры — Пошаговые уроки рисования
Что такое невозможный куб? Эта оптическая иллюзия, также называемая иррациональным кубом, была создана голландским художником М.С. Эшером в 1958 году. Его литографическая печать « Бельведер» изображает здание, основанное на невозможном кубе, которое, кажется, бросает вызов законам геометрии.
Невозможный куб определяется как «двумерная фигура, внешне напоминающая перспективный чертеж трехмерного куба, элементы которого непоследовательно нарисованы так, как они выглядят в реальном кубе». Другими словами, изображение выглядит как куб, который соединяется и перекрывается невозможным образом.
Невозможный куб связан с кубом Неккера — чертежом, на котором передняя грань куба может выглядеть как один из двух разных квадратов, в зависимости от того, как вы на него смотрите.
Пересечение верхней балки невозможного куба напоминает одну ориентацию куба Неккера, а нижние — как другую.
Многие художники экспериментировали с невозможным кубом, часто создавая отвлекающие оптические иллюзии. Некоторые статуи даже соответствуют этому описанию, если смотреть под определенным углом. В 1966 году в журнале Scientific American была показана фотография, изображающая невозможный куб .
Как работают оптические иллюзии, подобные этой? Человеческий глаз имеет тенденцию воспринимать двухмерные рисунки как трехмерные объекты. Поэтому линии на бумаге, кажется, представляют собой настоящий, осязаемый объект.
Иллюзии также полагаются на то, что мы уже знаем о мире. Наш глаз может быть обманут в применении общей геометрии или размеров к изображению. В случае невозможного куба мы делаем предположения о прямых углах и прочности балок.
Хотите нарисовать невозможный куб? Это простое пошаговое руководство по рисованию куба поможет вам. Все, что вам нужно, это карандаш, лист бумаги и ластик. Вы также можете покрасить свой законченный рисунок.
Вы также можете покрасить свой законченный рисунок.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Бейсбол, Футбол и Футбольный шлем.
Пошаговая инструкция по рисованию невозможного куба
1. Начните рисовать три прямые, вертикальные линии. Линии должны быть одинаковой длины, но средняя линия должна располагаться ниже, чем остальные. Затем соедините линии внизу, используя прямые линии. Это формирует боковые и нижние края куба.
2. Нарисуйте четырехугольник или четырехстороннюю форму в верхней части куба.
3. Далее подробно опишите верхнюю панель куба. Нарисуйте меньший квадрат в верхней части куба. Протяните короткую прямую линию от самого верхнего угла этого квадрата. Затем нарисуйте две прямые линии, идущие от этой линии, параллельно сторонам квадрата.
4. Нарисуйте квадрат внутри одной из боковых панелей куба.
ДРУГИЕ ЛЕГКИЕ РУКОВОДСТВА ПО ЧЕРТЕЖАМ:
5. Нарисуйте квадрат в оставшейся боковой панели куба.
Нарисуйте квадрат в оставшейся боковой панели куба.
6. Нарисуйте короткие прямые линии, идущие от противоположных углов квадратов. Затем нарисуйте две прямые линии, идущие от каждой из коротких линий. Эти линии должны быть параллельны сторонам квадрата.
7. Вытяните три прямые линии из нижнего левого угла куба. Затем вытяните три прямые линии из нижнего правого угла куба. Позвольте нижней и средней линии встретиться. Затем соедините концы линий, образуя прямоугольники.
8. Сотрите направляющие линии из фигур, нарисованных на предыдущем шаге
ДРУГИЕ ЛЕГКИЕ РУКОВОДСТВА ПО ЧЕРТЕЖАМ:
9. Нарисуйте последнюю сторону невозможного куба. Нарисуйте три прямые, параллельные линии, соединяющие верхний и нижний задние углы куба.
10. Раскрась свой невозможный куб.
Ознакомьтесь с нашими руководствами по рисованию искусственных объектов для получения дополнительной информации
Полное руководство по рисованию невозможного куба в одном изображении
Понравилось руководство по рисованию?
Оставьте комментарий ниже или следуйте на Pinterest.
Как нарисовать 3D-куб с помощью Matplotlib в Python?
В этой статье мы будем иметь дело с трехмерными графиками кубов с использованием matplotlib и Numpy. Кубы — одна из самых основных трехмерных фигур. Куб — это трехмерный твердый объект, ограниченный 6 одинаковыми квадратными гранями. Куб имеет 6 граней, 12 ребер и 8 углов. Все грани — квадраты одинакового размера. Общая площадь поверхности куба равна сумме площадей шести одинаковых квадратов.
Matplotlib поставляется с большим разнообразием графиков. Графики помогают понять тенденции, модели, чтобы сделать корреляции. Matplotlib был представлен для двумерного построения графиков. Трехмерный график включается путем импорта набора инструментов mplot3d, который поставляется с вашей стандартной библиотекой Matplotlib. После импорта 3D-графики можно создавать, передав ключевое слово «проекция = «3d» любой из функций создания обычных осей в Matplotlib.
Необходимые модули
- Matplotlib: Это библиотека построения графиков для программирования на Python, она служит служебной библиотекой визуализации, Matplotlib построена на массивах NumPy и предназначена для работы с более широким стеком SciPy.

- Numpy: Это универсальный пакет для обработки массивов. Он предоставляет высокопроизводительный многомерный массив и матрицы, а также большой набор высокоуровневых математических функций.
- mpl_toolkits: Предоставляет некоторые базовые инструменты трехмерного построения (разброс, серфинг, линия, сетка). Это набор вспомогательных классов для отображения трехмерных осей в Matplotlib.
Подход
Шаг 1: Импорт библиотек.
импортировать matplotlib.pyplot как plt из mpl_toolkits.mplot3d импортировать Axes3D импортировать numpy как np
Шаг 2: На этом шаге мы выбираем 3D-ось измерения X = 5, Y = 5, Z = 5, а в np.ones() мы передаем размеры куб.
# Создать ось оси = [5, 5, 5] # Создать данные data = np.ones(axes)
Шаг 3: На этом шаге мы выбираем непрозрачность цвета как альфа = 0,9 (варьируется от 0,0 до 1,0). На следующем шаге мы передаем размерность осей (т.
# управление Прозрачность альфа = 0,9 # контрольный цвет цвета = np.empty (оси + [4]) colors[0] = [1, 0, 0, альфа] # красный colors[1] = [0, 1, 0, альфа] # зеленый colors[2] = [0, 0, 1, альфа] # синий colors[3] = [1, 1, 0, альфа] # желтый colors[4] = [1, 1, 1, альфа] # серый
Шаг 4: На этом этапе мы использовали функцию figure() библиотеки matplotlib, которая используется для создания новой фигуры. После этого мы использовали метод add_subplot() для добавления осей к фигуре. как трехмерная (т.е. проекция = ‘3d’) часть расположения сюжета. Он имеет 3 аргумента.
- Количество строк в сетке,
- Количество столбцов в сетке и,
- Позиция, в которой должен быть размещен новый участок.
Следует отметить, что fig.add_subplot(1, 1, 1) эквивалентен fig.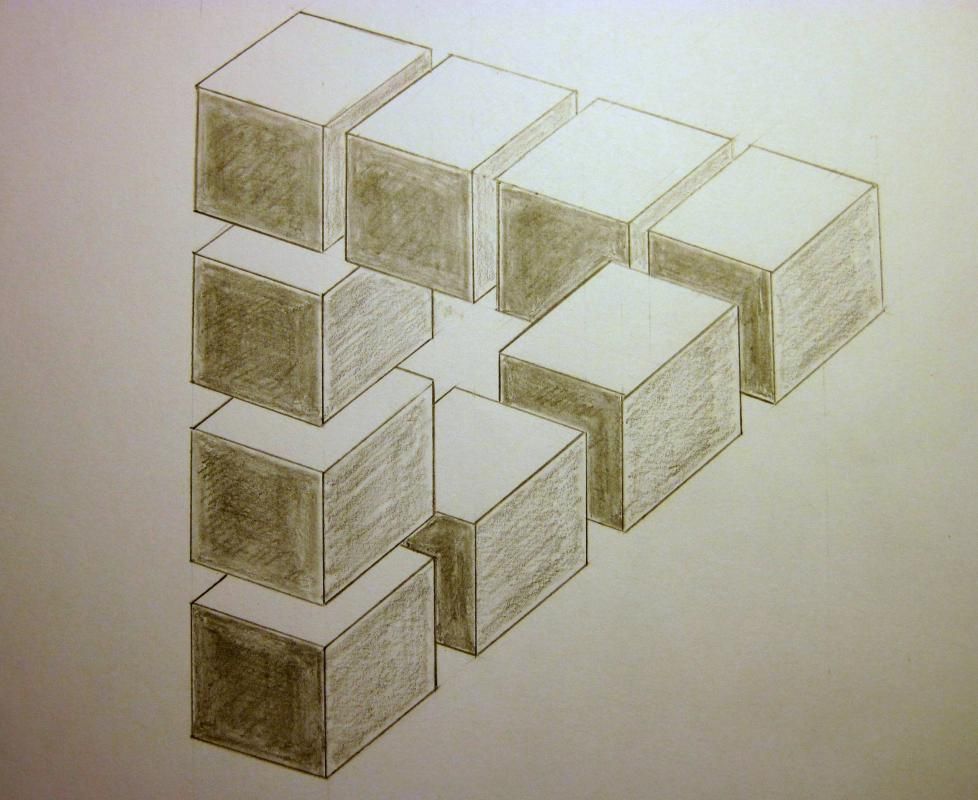 add_subplot(111).
add_subplot(111).
# Рисунок графика рис = plt.figure() ax = fig.add_subplot(111, project='3d')
Шаг 5: И на этом последнем шаге воксели используются для настройки размера, положения и цвета сетки. Правильный синтаксис приведен выше.
# Воксели используются для настройки # размеры, позиции и цвета. ax.voxels(data, facecolors=colors, edgecolors='grey')
Пример 1: Простой кубик одного цвета.
Здесь изменение цветов[ : ] означает, что мы выбираем все элементы массива как один цвет (т.е. красный), и чтобы удалить сетку, мы удалили параметр «edgecolor» из метода вокселей, чтобы иметь просто один цветовой куб.
Python3
|
Выход:
Пример 2:
Куб с сеткой и разной цветом
Python3
|
Output:
Пример 3: Куб с гранями вдоль оси Y
В этом примере мы добавим еще одну строку кода view_init(), чтобы изменить вид оси по своему усмотрению. Функция view_init() может использоваться для программного изменения представления осей. Здесь мы используем elev=100 и азим=0.
Функция view_init() может использоваться для программного изменения представления осей. Здесь мы используем elev=100 и азим=0.
Синтаксис: view_init(elev, azim)
Параметры:
- ‘elev’ хранит угол возвышения в плоскости z.
- «azim» хранит угол азимута в плоскости x, y.
Python3
 0084 0084 = '3d' )
|
Output:
Пример 4: куб с гранями вдоль оси X
Функция view_init() может использоваться для программного изменения вида осей. Здесь мы используем elev=100 и azim=90.
Python3
4444444444444444444444444444444444444444444444444444444444444444444.0083]
|
Выход:
Изометрический инструмент для рисования
Оценка: с 3 по 5, с 6 по 8, средняя школа
Используйте этот интерактивный инструмент для создания динамических рисунков на изометрической точечной бумаге. Рисуйте фигуры, используя ребра, грани или кубы. Вы можете сдвигать, вращать, раскрашивать, разбирать и просматривать в 2D или 3D. Начните с нажатия на куб вдоль левой стороны; затем поместите кубики на сетку, где вы хотите.
Этот интерактив оптимизирован для настольных компьютеров и планшетов.
- Выберите куб , грань или сегмент вдоль левой навигации.
- Затем поместите объект в нужное место на сетке. Если ваш выбор красный, на сетке, то это место, где вы не можете разместить объект.
ПОДСКАЗКА
- Нарисуйте свою фигуру сзади вперед и снизу вверх, чтобы обеспечить правильное выравнивание кубов.

- При добавлении смежных кубов не забудьте нажать на грань куба, которого хотите коснуться.
Режим создания
Существует два способа перемещения объектов:
- Использование стрелы . Просто выберите и перетащите объект(ы) в новое место.
- Кнопки перемещения юнитов
Другие кнопки в верхней части навигации выполняют различные функции:
Вращайте всю фигуру, перетаскивая изображение или используя ползунки.
Используйте ластик для стирания отдельных объектов. Вы также можете выбрать несколько объектов с помощью указателя, а затем использовать ластик, чтобы стереть эти объекты.
Взорвать — превратить все кубы в грани. Если два куба имеют общую грань, грань не будет отображаться. Обратите внимание, что вы не можете отменить это действие.
Используйте кисть , чтобы выбрать цвет перед созданием объекта. Вы также можете изменить цвет после создания объекта, выбрав объект нужного вам цвета.
Режим проверки
В режиме проверки вы можете:
- Просматривать 3D- или 2D-версию вашего изометрического чертежа.
- Распечатайте изометрический чертеж так, как он показан в рабочей области.
- Поверните изометрический рисунок.
- Выберите отображение изометрического чертежа с осью или без нее.
- Выберите отображение сплошного или прозрачного изометрического чертежа.
Вы можете сбросить весь вид в любой момент, нажав кнопку Сбросить вид .
На рисунке ниже показаны три вида фигуры: спереди, справа и сверху. Вся фигура использует в общей сложности семь кубов. Можете ли вы построить фигуру с помощью инструмента изометрического рисования? (Обязательно используйте кубики соответствующего цвета.)
Каков объем этой фигуры? Какова площадь его поверхности?
Стандарты и ожидания NCTM
- Геометрия / измерения
- Поймите, что по сходству отношения сторон в прямоугольных треугольниках являются свойствами углов в треугольнике, что приводит к определениям тригонометрических соотношений для острых углов.



 ones(axes, dtype
ones(axes, dtype  voxels(data, facecolors
voxels(data, facecolors  ONE0083 )
ONE0083 )  0084
0084  ones( axes, dtype
ones( axes, dtype 
 view_init(
view_init( 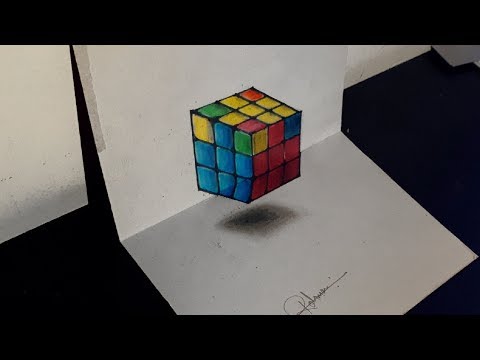 empty(axes
empty(axes  0084
0084  add_subplot(
add_subplot(  view_init(
view_init( 

Leave a Comment