Как начертить эллипс циркулем пошагово: Как начертить эллипс

20.07.2023 Разное

Содержание

Построение биссектрисы угла / Построения циркулем и линейкой / Треугольники / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Треугольники
Построения циркулем и линейкой
Построение биссектрисы угла

Пример:

Построить биссектрису данного угла.

Дано: А.

Построить: биссектрису А.

Решение:

Произвольно строим с помощью линейки А.

С помощью циркуля строим окружность произвольного радиуса с центром в вершине А.

Точки пересечения данной окружности со сторонами А обозначим В и С.

Теперь проведем две окружности одинакового радиуса ВС с центрами в точках

В и С.

В зависимости от длины ВС, получим одну или две точки пересечения данных окружностей внутри А. Ту точку, которая лежит внутри угла обозначают буквой и проводят через нее луч с началом в точке А. В нашем случае, получилось две точки пересечения данных окружностей, которые лежат внутри А. Обозначаем одну из них Е и проводим с помощью линейки луч АЕ.

Докажем, что луч АЕ является биссектрисой данного А. Рассмотрим треугольники АВЕ и АСЕ.

В данных треугольниках АВ = АС как радиусы окружности с центром в точке А

, ВЕ = СЕ по построению, АЕ — общая, следовательно, АВЕ =АСЕ по 3 признаку равенства треугольников, откуда следует, что ВАЕ =САЕ, т.

е луч АЕ — биссектриса данного А. Что и требовалось доказать.

Замечание:

С помощью циркуля и линейки можно разделить данный угол на два равных угла, для этого нужно провести его биссектрису.
С помощью циркуля и линейки можно разделить данный угол на четыре равных угла, для этого нужно разделить угол пополам (на два равных угла), а затем каждую половину разделить пополам еще раз.

С помощью циркуля и линейки нельзя разделить данный угол на три равных угла (задача о трисекции угла).

Советуем посмотреть:

Построение угла, равного данному

Построение перпендикулярных прямых

Построение середины отрезка

Среднее пропорциональное

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 152, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 175, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 319*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 356, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 357, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 362, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 586, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 900, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1144, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Построение правильных многоугольников — Техническое черчение

Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

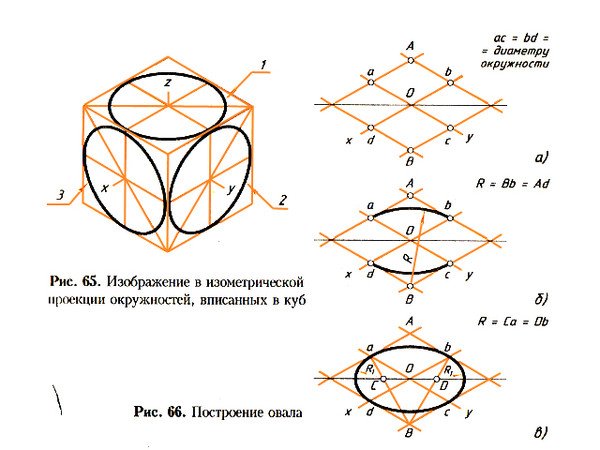
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Как нарисовать эллипс

Блог

Боб Миллер утверждает, что с помощью нескольких простых формул и умного приспособления становится возможным рисовать и вырезать эллипсы любого размера и добавлять эту величественную и приятную форму в вашу работу.

Боб Миллер 02 октября 2019 г.

Эллипс — это особый вид овала, на самом деле это самый величественный и изысканный из овалов. Что отличает эллипс от других овалов, так это то, что его можно определить математически и нарисовать механически. Большинство людей посмотрят на эллипс и просто назовут его овалом, но это еще не все. С помощью нескольких простых формул и умного приспособления вы можете рисовать и вырезать эллипсы любого размера и добавлять эту величественную и приятную форму в свою работу.

Что делает эллипс особенным, так это две точки внутри формы, называемые «фокусами» (множественное число от «фокуса»). Их важность заключается в том, что расстояние между фокусом, краем и другим фокусом постоянно для любой точки периметра эллипса. Это не только приводит к элегантной и приятной форме, но также позволяет точно и легко рисовать эллипс.

Поскольку эллипс можно определить математически, здесь вступают в дело некоторые математические расчеты. Но не беспокойтесь; ты можешь это сделать. Все, что вам нужно знать, это общий размер эллипса, определяемый его длиной и шириной в максимальных точках. Эти два измерения называются большой осью и малой осью. Отсюда можно найти расположение очагов, используя эту формулу:

C=√(A ² -B ² )

, где C равно расстоянию между центром и каждым из фокусов, A равно радиусу большой оси, а B равно радиусу малой оси. См. диаграмму ниже, чтобы увидеть, что и куда.

Как только вы узнаете, где расположены фокусы относительно центра эллипса, рисование эллипса становится простой задачей.

Просто вбейте два гвоздя в узор в фокусах и завяжите петлю из неэластичной нити, которая зацепится за оба фокуса и при натяжении достанет до любой точки эллипса. Затем, просто удерживая натянутой петлю веревки, перемещайте карандаш вокруг фокусов, позволяя веревке направлять ваш путь. Поскольку длина нити фиксирована, она будет удерживать карандаш на равном расстоянии от обоих фокусов и аккуратно и четко определять эллипс. На следующей схеме и видео показано, как это работает.

В то время как струнный метод отлично подходит для чертежей и компоновки, для того, чтобы на самом деле вырезать точный эллипс, вам понадобится эллипсограф, хитрое приспособление, которое может двигаться в эллиптической форме и переносить что угодно, от карандаша до фрезера. Эллипсограф довольно прост; все, что требуется, это две направляющие из МДФ, расположенные перпендикулярно друг другу. Затем два куска твердой древесины фрезеруются до скользящей посадки в гусеницах, а в их центры добавляется болт.

Прикрепите к обоим болтам жесткий фанерный рычаг. Чтобы контролировать размер эллипса, вам нужно знать большой и малый радиусы эллипса (A и B из приведенной выше формулы).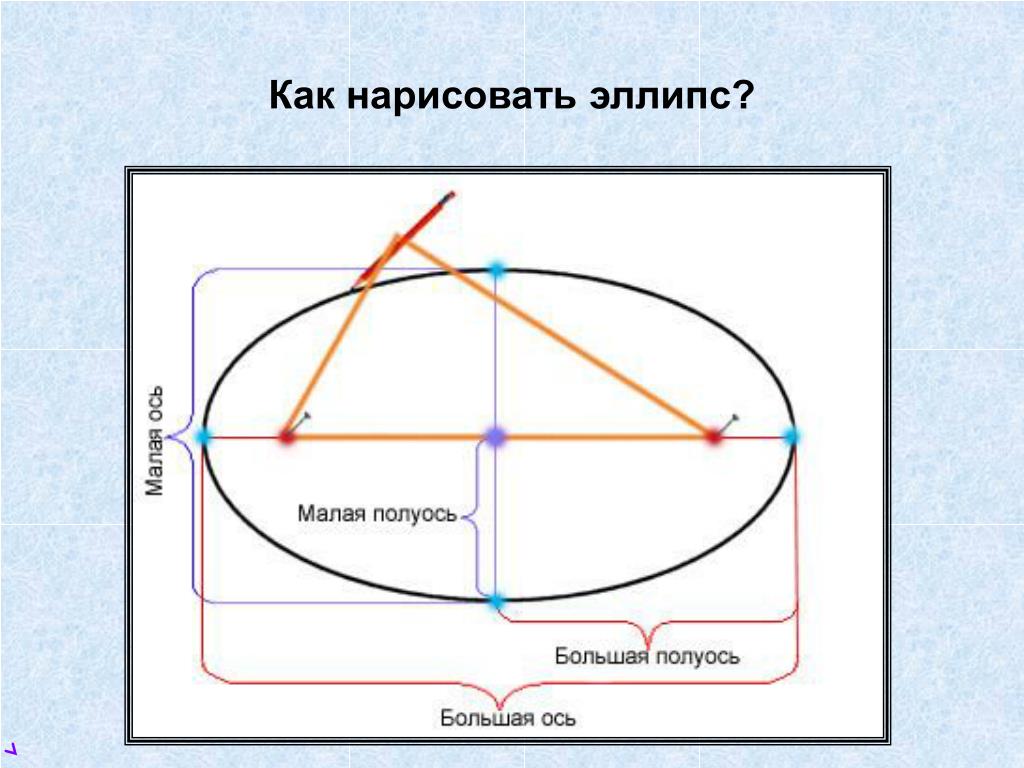 Прикрепите фрезер к фанерному рычагу, а затем прикрепите его к двум скользящим блокам. Прикрепите один блок на меньшем расстоянии от маршрутизатора, а другой — на большем расстоянии от маршрутизатора. Когда вы перемещаете руку по эллипсу, два ползунка будут обходить друг друга в зажимном приспособлении и перемещать конец руки по идеальному эллипсу!

Не бойтесь эллипса и не бойтесь математических расчетов, чтобы это произошло.

Получите все!

НЕОГРАНИЧЕННОЕ Членство — это как пройти мастер-класс по деревообработке за меньшие деньги чем 10 долларов в месяц.

Избранные проекты и планы

Буфет Криса Гочнура сочетает в себе практичность, прочность и красоту в современном корпусе

Основные моменты

Развивайте свои навыки
при подписке на нашу электронную почту
Смотреть все рассылки
Наш подкаст, выходящий раз в две недели, позволяет редакторам, авторам и специальным гостям отвечать на ваши вопросы по деревообработке и связаться с онлайн-сообществом по деревообработке.
Мы создали эти специальные коллекции контента, организованные для того, чтобы дать вам возможность глубоко погрузиться в ряд тем, которые имеют значение.
Присоединяйтесь к нашим доверенным экспертам для углубленного онлайн-обучения.

Посмотреть все

Посмотреть Другие продукты

Как рисовать эллипсы от руки

Не знаете, как рисовать эллипсы от руки?
Следуйте этому простому руководству и узнайте, как быстро рисовать идеальные эллипсы!

В сегодняшнем видеоуроке мы рассмотрим:

5 типичных ошибок новичков.
8 простых способов преуспеть в ваших эллипсов уже сегодня!

Возьмите шариковую ручку и бумагу, и давайте вместе нарисуем 10000 эллипсов! 😀

«Я боюсь не того, кто отработал 10 000 ударов один раз,
, а того, кто отработал один удар 10 000 раз».
– Брюс Ли

Как рисовать эллипсы от руки

Сообщение, которое я получил от Сэма:

Теперь Сэм может успешно рисовать эллипсы

01:01 ОШИБКА №1 🥞 ЭЛЛИПС БЛИН

эллипс, который выглядит плоским внизу.
Вы пытаетесь нарисовать их много, но эта плоская поверхность продолжает возвращаться.

Блинный эллипсОни не годятся для рисования, но выглядят восхитительно

01:23 ОШИБКА №2 ТОЧЕЧНЫЙ ЭЛЛИПС

Форма эллипса становится «яйцом»?

Заостренный эллипс. Форма яйца — вторая по распространенности ошибка новичков.

01:58 ОШИБКА №3 ПЕСИСТЫЙ ЭЛЛИПС

Неуверенный в себе, вы проводите множество маленьких линий одну за другой.
Но результат выглядит любительским и нерешительным.

Пушистый эллипс

02:27 ОШИБКА № 4 ШАТКИЙ ЭЛЛИПС

Недостаток уверенности, твоя рука дрожит.
Вы чувствуете немного страха когда рисуете.

Шаткий эллипс

02:35 ОШИБКА №5 СВЕРХУВЕРЕННЫЙ ЭЛЛИПС

Наоборот, вы хотите подражать профессиональным скетчерам.
Вы рисуете быстро, и ваши линии выражают скорость.
Но… ни один эллипс не получится правильно нарисовать.

Рисовать самоуверенно — это все равно, что пытаться водить спортивный автомобиль, который слишком быстр для вас. Сначала вам нужно пройти обучение основам.

03:25 КАК РЕШИТЬ 5 ОШИБОК ЭЛЛИПСА

Мы рассмотрели 5 распространенных ошибок начинающих.
А теперь давайте рассмотрим 8 дополнительных техник, которые помогут уверенно освоить эллипсы от руки!

03:41 РЕШЕНИЕ #1 ПРИЗРАЧНОЕ РИСОВАНИЕ

Если вы хотите научиться рисовать как профессионалы,
эту технику очень важно освоить как можно раньше (для рисования «идеальных» линий, кругов и кривых)

Моделирование движения перед отрисовкой эллипса помогает лучше визуализировать результат. Не останавливайтесь на первой петле эллипса.

0123

5:00 РЕШЕНИЕ #2 РИСОВАТЬ НЕЖНО

Если у вас тяжелое запястье,
пора быть аккуратнее с пером.

Используйте фантомный рисунок и постепенно касайтесь кончиком шариковой ручки поверхности бумаги. Затем смело по пути, если это необходимо.

05:53 РЕШЕНИЕ №3 ОБЫЧНАЯ СКОРОСТЬ

Если вы начинаете рисовать, избегайте ускорения, чтобы показать плавность.
Вам также не нужна скорость, чтобы рисовать динамические линии.
Не торопитесь.
Важен импульс, который вы создаете во время рисования призрака, а не скорость.

06:30 РЕШЕНИЕ #4 ИТЕРАЦИЯ

Если вы чувствуете, что начинаете рисовать плохой эллипс, не останавливайтесь!
Продолжить и повторить поверх него. Если он еще не устраивает, нарисуйте еще один !

08:52 РЕШЕНИЕ №5 РИСУНОК ВСЕЙ РУКИ

Вы рисуете, опираясь локтем на стол?
Если да, приготовьтесь добиться больших успехов, начав рисовать всей рукой.

11:04 РЕШЕНИЕ №6 ХОРОШАЯ ПОДДЕРЖКА

Чтобы рисовать точно, нужна стабильность.
Вы используете кончик пальца ниже, чтобы «держать перо как штатив».
Таким образом, когда вы рисуете, ваши пальцы скользят по поверхности бумаги, сохраняя при этом контроль и устойчивость.

12:18 РЕШЕНИЕ №7 СИММЕТРИЯ

Красивый эллипс симметричен.
Чтобы начать это упражнение, давайте посмотрим, как их нарисовать!

Избегайте формы яйца, начав сначала рисовать малую ось. Рисование с помощью º значительно упрощает движение, поскольку оно учитывает движения вашего тела. Практикуйтесь рисовать только под одним углом, чтобы хорошо освоить его. Не забывайте поворачивать бумагу в любое время, когда вам нужно

16:23 РЕШЕНИЕ № 8 ФОКУС

Легко запутаться в таком количестве эллипсов на бумаге. Ваше зрение становится размытым, а ваши эллипсы наклоняются.

Визуализируйте угол малой оси , прежде чем рисовать эллипсы.

Comments

Leave Comment

Как начертить эллипс циркулем пошагово: Как начертить эллипс