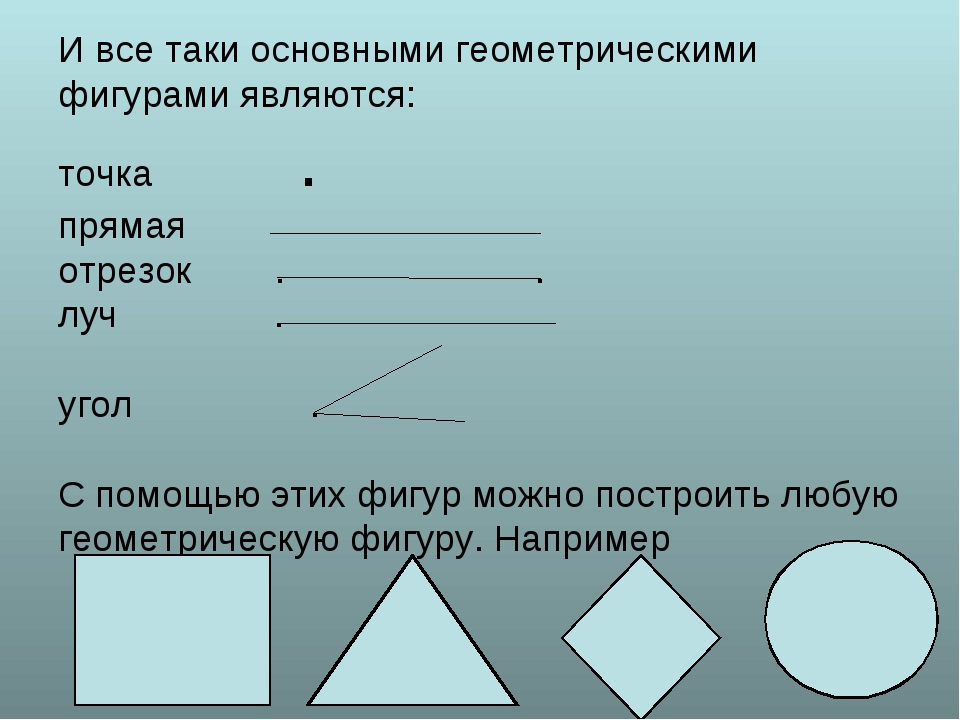
Фигуры основные: Основные понятия, аксиомы и теоремы стереометрии
21.10.2019 


 Разное
Разное
Основные понятия, аксиомы и теоремы стереометрии
Основные понятия стереометрии
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.
Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.
Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.
Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы.
Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.
Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).
Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды.
Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).
Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).
Аксиомы стереометрии
Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.
Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.
Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.
Следствия из аксиом
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.
Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна.
Следствие 4. Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.
Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.
Основные теоремы стереометрии
Теоремы о параллельности прямых и плоскостей
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут: a // βТеорема 1: Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.
Теорема 2: Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.
Теорема 3: Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.
Теорема 4: Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A1 B1 и C1 D1 другой плоскости, то эти плоскости параллельны.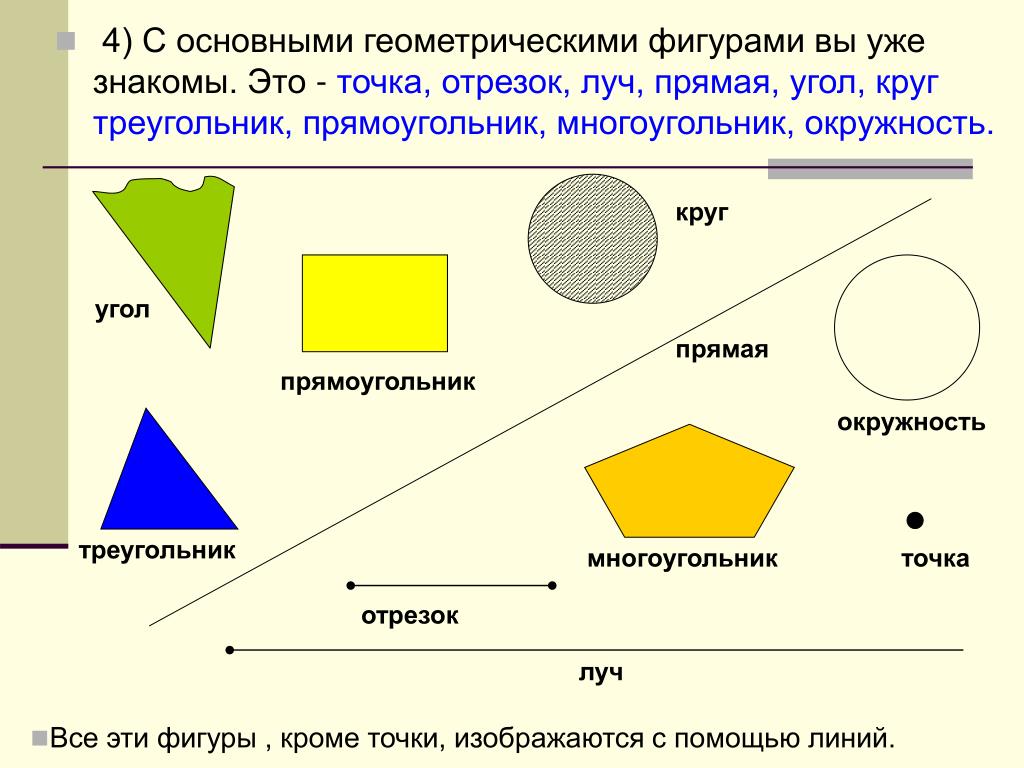
Теоремы о перпендикулярности прямых и плоскостей
Теорема 1: Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.Теорема 2: Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P (Достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: AC, BC, DE).
Теорема 3: Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.
Теорема 4: Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.
Теоремы о перпендикулярности плоскостей
Двугранный угол называется прямым, если его линейный угол прямой. Прямой двугранный угол равен смежному с ним двугранному углу.
Определение: Две плоскости называются взаимно перпендикулярными, если они образуют прямые двугранные углы.
Теорема 1:Перпендикулярность прямых в пространстве. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они то же перпендикулярны.
Теорема 2: Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Следствие 1: Если из точки одной из двух взаимно перпендикулярных плоскостей проведен перпендикуляр к другой плоскости, то он принадлежит первой плоскости.
Следствие 2: Если две плоскости, перпендикулярные к третьей плоскости, пересекаются, то их линия пересечения есть перпендикуляр к этой плоскости.
Теорема о скрещивающихся прямых
Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.Теорема 1: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.
Доказательство
Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.
Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость — α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.
Теорема 2: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство.
Пусть нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.
Проведем через точку А прямую АЕ, параллельную прямой DC (Рис.
Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямая DC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α – единственная. Теорема доказана.
Теорема о трех перпендикулярах
Теорема 1: Теорема о трех перпендикулярах. Верно и обратное утверждение:
Верно и обратное утверждение:Теорема 2: (о трех перпендикулярах). Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость.
Доказательство.
Пусть AB — перпендикуляр к плоскости a, AC — наклонная и c — прямая в плоскости
Взаимное расположение прямых в пространстве
Прямые в пространстве могут лежать в одной плоскости или в разных плоскостях.
- Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
- Две прямые в пространстве называются пересекающимися, если они лежат в одной плоскости и имеют общую точку.
- Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости
Основные фигуры в стереометрии
Симметрия фигур
- Точки M и M1 называются симметричными относительно точки O, если O является серединой отрезка MM1.
- Точки M и M1 называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM1 и перпендикулярна ему.
- Точки M и M1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM1 и перпендикулярна этому отрезку.
- Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.

- Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.
Двугранный угол
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).
Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.
Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.
Две плоскости называются перпендикулярными, если угол между ними равен 90°.
Теоремы:
Теорема 1: (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема 2: Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.
Призма
Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях.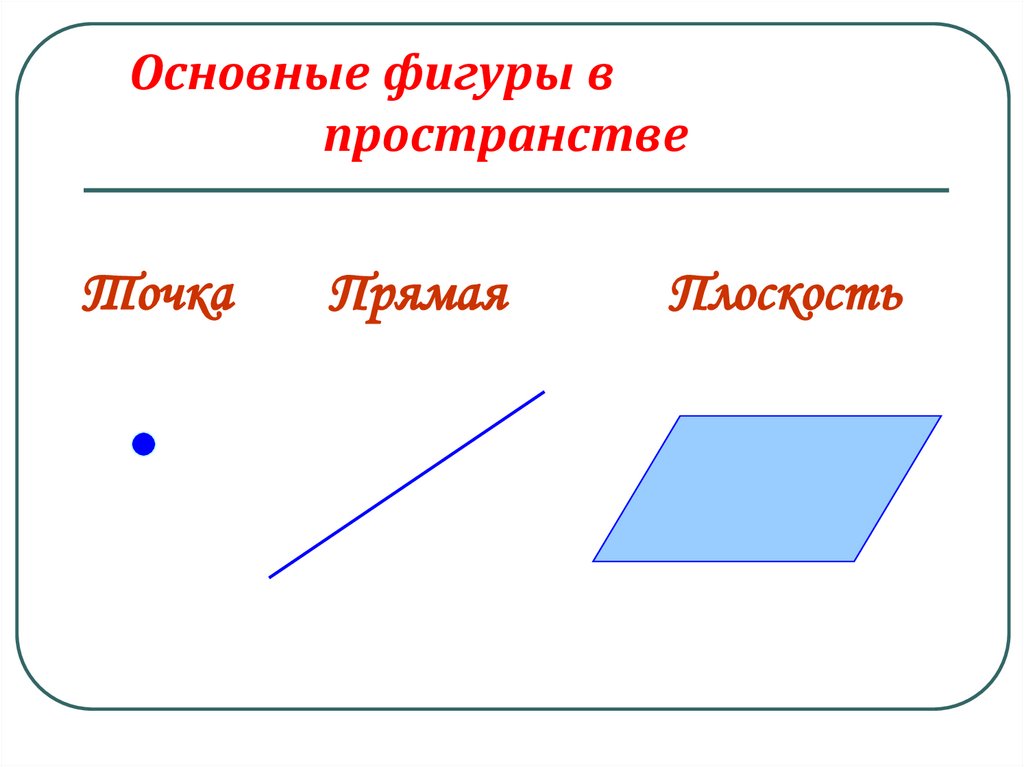 На чертеже это: ABCDE и KLMNP.
На чертеже это: ABCDE и KLMNP.
Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
Боковая поверхность – объединение боковых граней.
Полная поверхность – объединение оснований и боковой поверхности.
Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
На чертеже это, например, EBLP.
Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру. Площадь поверхности и объём призмы.
Площадь поверхности и объём призмы
Свойства призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания
Параллелепипед
Параллелепипедом называется призма, основанием которой служит параллелограмм.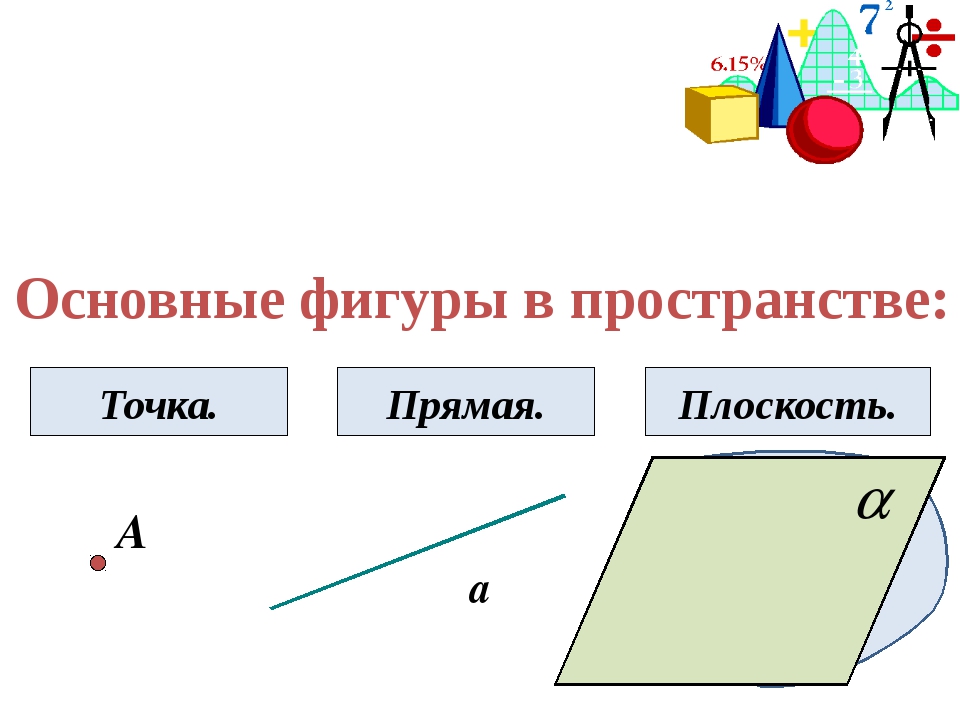
Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны – ребрами, а вершины параллелограммов – вершинами параллелепипеда.
У параллелепипеда все грани — параллелограммы.
Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани ― боковыми гранями параллелепипеда.
Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда. A1 H h2 A2 An A3 B1 B2 n B3 B A B C D A1 B1 C1 D1 7
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.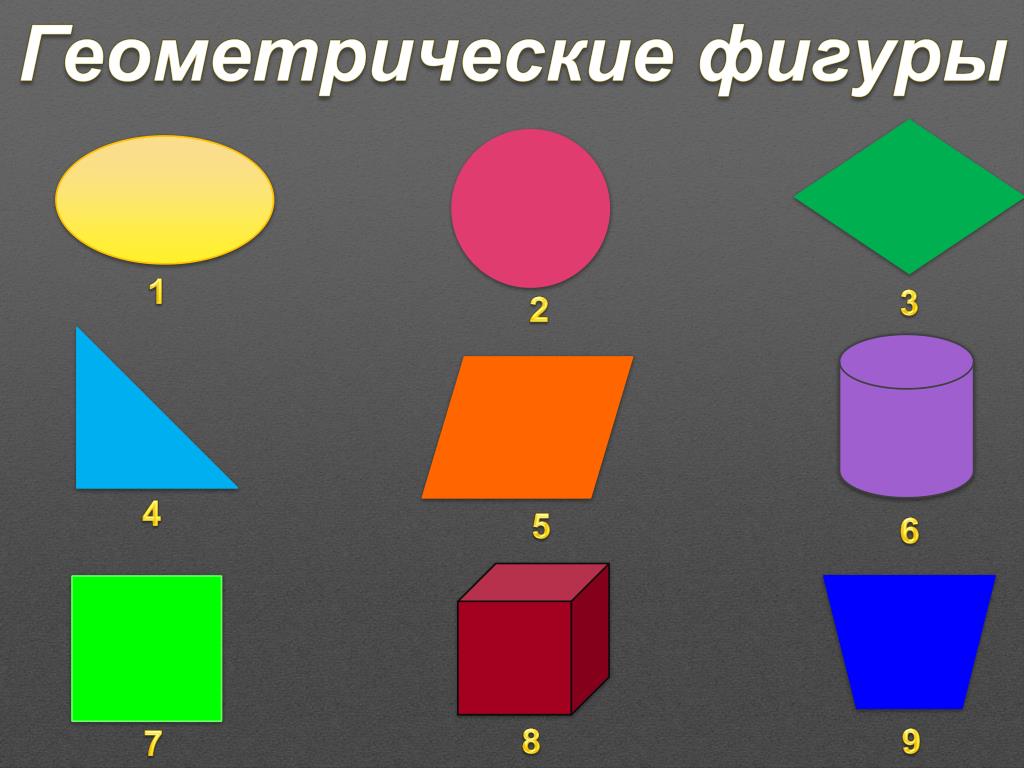
Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
Свойства параллелепипеда:
1. Противоположные грани параллелепипеда равны и параллельны.
2. Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Боковые грани прямого параллелепипеда — прямоугольники.
4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Диагонали прямоугольного параллелепипеда равны.
Пирамида
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее.Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.
Грани, отличные от основания, называются боковыми.
Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины).
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H.
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины.
Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания.
Свойства пирамиды:
1. Боковые ребра пирамиды равны.
2. Боковые ребра пирамиды одинаково наклонены к основанию пирамиды.
3. Вершина пирамиды проектируется в центр окружности, описанной около основания пирамиды.
4. Высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны, а высота пирамиды лежит внутри пирамиды.
5. Все двугранные углы при основании пирамиды равны.
6. Вершина пирамиды проектируется в центр окружности, вписанной в основание.
7. Высоты всех боковых граней пирамиды, проведённые из вершины пирамиды, равны, а высота пирамиды лежит вне пирамиды.
8. Двугранные углы между боковыми гранями и плоскостью основания пирамиды равны.
9. Вершина пирамиды проектируется в центр окружности, вневписанной в основание пирамиды.
Правильная пирамида
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.Свойства правильной пирамиды:
1. В правильной треугольной пирамиде противоположные ребра попарно перпендикулярны.
2. Боковые ребра правильной пирамиды равны между собой.
3. Двугранные углы при основании правильной пирамиды равны между собой.
4. Двугранные углы при боковых рёбрах правильной пирамиды равны.
Тетраэдр
Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.Тетраэдр называется правильным, если все его грани – равносторонние треугольники.
Свойства тетраэдра:
1. Все ребра правильного тетраэдра равны между собой.
2. Все грани правильного тетраэдра равны между собой.
3. Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.
Прямоугольная пирамида
При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид.Усечённая пирамида
Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.Свойства усечённой пирамиды:
1. Основания усечённой пирамиды — подобные многоугольники.
2. Боковые грани усечённой пирамиды — трапеции.
3. Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.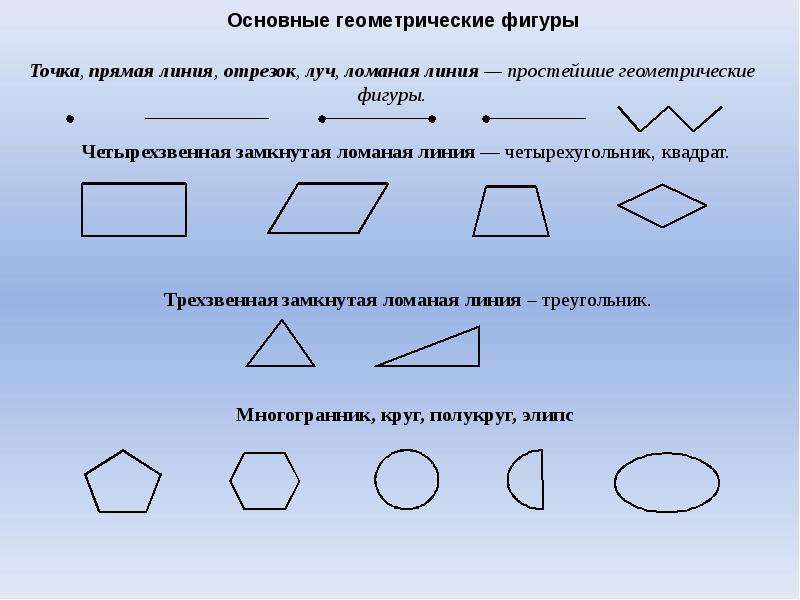
4. Боковые грани правильной усечённой пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
5. Двугранные углы при боковых рёбрах правильной усечённой пирамиды равны.
Сфера и шар
Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.Хордой сферы называется отрезок, соединяющий две точки сферы.
Диаметром сферы называется хорда, проходящая через ее центр. Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.
Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра.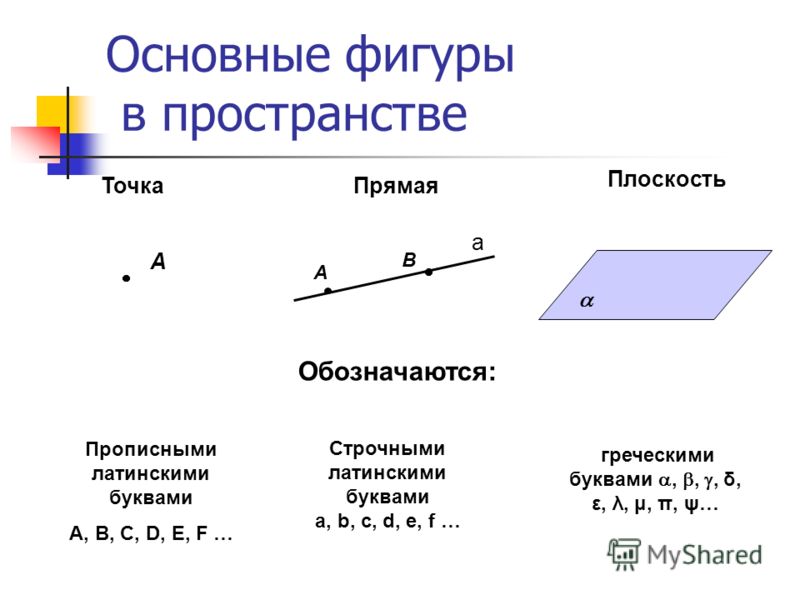 Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра.
Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра.
Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.
Теорема 1: (о сечении сферы плоскостью). Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
Теорема 2: (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.
Доказательство
Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.
Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.
Теорема 1: (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
Теорема 2: (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.
Многогранники
Геометрическим телом (или просто телом) называется ограниченная связная фигура в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры. Границу геометрического тела называют также его поверхностью и говорят, что поверхность ограничивает тело.Плоскость, по обе стороны которой имеются точки данного тела, называется секущей плоскостью.
Фигура, которая образуется при пересечении тела плоскостью, называется сечением тела.
Многогранником или многогранной поверхностью называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Тело, ограниченное многогранником, часто также называют многогранником.
Тело, ограниченное многогранником, часто также называют многогранником.
Многоугольники, из которых составлен многогранник, называют его гранями. Стороны граней называются ребрами, а концы ребер — вершинами многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранники бывают выпуклые и невыпуклые.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками.
Свойства многогранников:
1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.
3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.
4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.
Правильные многогранники
Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники, и в каждой его вершине сходится одно и то же число ребер.Все ребра правильного многогранника равны, все двугранные углы правильного многогранника равны, все многогранные углы правильного многогранника равны.
Существует ровно пять выпуклых правильных многогранников:
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, и в каждой вершине многогранника сходится одно и то же число ребер. Все ребра правильного многогранника равны друг другу. Равны также все его двугранные углы, содержащие две грани с общим ребром.
1.Правильный тетраэдр (четырехгранник) ― многогранник, составленный из четырех правильных треугольников.
2. Правильный гексаэдр (шестигранник) или куб ― многогранник, составленный из шести правильных четырехугольников (квадратов) .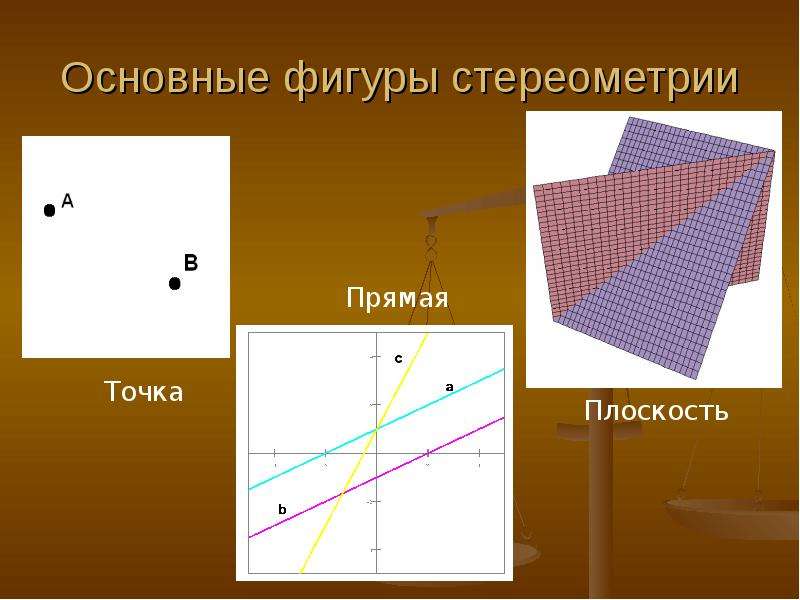
3. Правильный октаэдр (восьмигранник) ― многогранник, составленный из восьми правильных треугольников.
4. Правильный додекаэдр (двенадцатигранник) ― многогранник, составленный из двенадцати правильных пятиугольников.
5. Правильный икосаэдр (двадцатигранник) ― многогранник, составленный из двадцати правильных треугольников.
Цилиндр
В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности.Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.
Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.
Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.
Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.
Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.
Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.
Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.
В цилиндре высота равна образующей.
Радиусом цилиндра называется радиус его оснований.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.
Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.
Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.
Свойства цилиндра:
1. Основания цилиндра равны
2. Основания лежат в параллельных плоскостях
Основания лежат в параллельных плоскостях
3. Образующие цилиндра параллельны и равны
Для чего нужны геометрические фигуры. Часть 1
Пользу раннего развития сложно оспорить. Активное обучение способствует формированию креативной и гармоничной личности. С ранних лет малыш привыкает узнавать все новое, и в дальнейшем не будет проблем с усвоением информации.
1) изучение форм предметов помогает ребенку расширить кругозор, словарный запас и развивает наблюдательность
2) получение новых знаний – всегда тренировка для мозга
3) развитие логического мышления
4) развитие пространственного представления
5) совершенствование математических и аналитических способностей
6) развитие творческих способностей
7) тренировка ассоциативного мышления (малыш учится проводить аналогию)
С чего начать изучение?
Начать стоит с самых простых азов. В первую очередь познакомить малыша с кругом, треугольником и квадратом.
Самый простой и доступный способ – это показывать формы на примере бытовых предметов. Например: тарелка круглая, окно квадратное и т.д. Со временем затрагивайте не только мебель в доме, но и предметы на улице и детской площадке.
Для деток до 1,5 лет разговоры с мамой – отличный источник изучения окружающего мира. Даже если вам кажется, что малыш не обращает на это внимания, не прекращайте повторять. Любая информация при повторении обязательно запомнится малышу.
При правильном подходе, в 2 года детки смогут отличать:
-круг
-квадрат
-треугольник
И могут найти нужную фигуру среди других геометрических фигур.
К 3 годам можно добавить:
-овал
-ромб
-прямоугольник
В 4 года и старше – могут анализировать сложные картинки, состоящие из множества фигур
Игры с геометрическими фигурами.
1) В сумочку или непрозрачный пакет прячем фигуры. Ребенок берет в руки предмет и пытается определить его форму не глядя.
2) Попросите ребенка назвать формы, которые могут кататься, фигуры с углами и без.
3) Ассоциации. Пусть малыш расскажет, на что похож треугольник, круг, овал и другие фигуры.
Во время создания картин проговаривайте фигуры предметов. Например: «мы сделаем квадратный дом с треугольной крышей».
Изучаем фигуры с ребенком 2-3 года.
В этом возрасте дети уже знают цвета и ориентируются в размерах, поэтому для изучения фигур подходят следующие занятия:
1) Найди лишнее. Можно взять несколько квадратов и один треугольник. Малыш должен выбрать какой предмет отличается от других. Для усложнения можно узнать, почему он выбрал именно эту фигуру.
2) Разложи правильно. Можно взять 4 фигуры (например: 2 круга и 2 квадрата) и предложить ребенку разложить их в две стопки. Можно усложнить задание: взять 9 фигур и разложить на 3 стопки.
3) Сортировка. Используем фигуры разных размеров и цветов. Например: синие треугольники – в одну сторону, красные квадраты – в другую. Это занятие укрепит знание цветов и позволит лучше ориентироваться в размерах.
Например: синие треугольники – в одну сторону, красные квадраты – в другую. Это занятие укрепит знание цветов и позволит лучше ориентироваться в размерах.
4) Найди сокровище. Понадобится миска с любой крупой, в которой спрячьте различные фигурки. Когда малыш их будет находить, обязательно должен дать название найденному предмету. Такая игра не оставит равнодушным ни одного ребенка!
Объёмная фигура и геометрическое тело — урок. Геометрия, 10 класс.
Шар — геометрическое тело, его поверхность — сфера.
Шар Сфера
Винтовая линия — объёмная фигура, но это не тело.
Винтовая линия
Пирамида — геометрическое тело, которое ограничено плоскими многоугольниками.
Пирамида Плоские многоугольники
Плоскость
 В окружающем мире поверхность множества предметов подобна геометрической плоскости, например, пол в комнате, стол, поверхность воды в озере или бассейне. Большинство упомянутых предметов — прямоугольной формы; если разглядывать их с большого расстояния, то они напоминают параллелограммы. Поэтому довольно часто плоскость на рисунке изображается в виде параллелограмма, но её можно изобразить и по-другому — любой замкнутой линией.
В окружающем мире поверхность множества предметов подобна геометрической плоскости, например, пол в комнате, стол, поверхность воды в озере или бассейне. Большинство упомянутых предметов — прямоугольной формы; если разглядывать их с большого расстояния, то они напоминают параллелограммы. Поэтому довольно часто плоскость на рисунке изображается в виде параллелограмма, но её можно изобразить и по-другому — любой замкнутой линией.
Примеры плоскости в природе:
Поверхность стола Поверхность книг Поверхность воды Пол
В стереометрии так же, как и в планиметрии, определяется равенство двух геометрических тел или фигур.
Две фигуры (или тела) называются равными, если их можно совместить наложением.
Главная величина геометрических тел — это их объём.
Объём геометрического тела — это величина, которая описывает занимающую этим телом часть пространства.
Из определения следует, что объём не зависит ни от местонахождения тела в пространстве, ни от того, как это тело делится на части.
Величину объёма вычисляют, основываясь на аксиомах:
1) равные тела имеют равные объёмы.
2) Объём тела равен сумме объёмов его отдельных частей.
Чтобы объём можно было измерить, т. е. чтобы объём можно было бы выразить в виде числа, необходимо выбрать единицу измерения объёма.
Единица объёма — это объём такого куба, ребро которого равно одной единице длины.
Если ребро куба равно \(1\) \(см\), то его объём обозначается кубическими сантиметрами — см3, если ребро куба равно \(1\) \(м\), то объём обозначается кубическими метрами — м3.
Тела с равными объёмами называются равновеликими.
Равные тела Равновеликие тела
Равные тела с объёмом \(8\) см3 Равновеликие тела с объёмом \(6\) см3
Все равные тела равновелики, но не все равновеликие тела равны.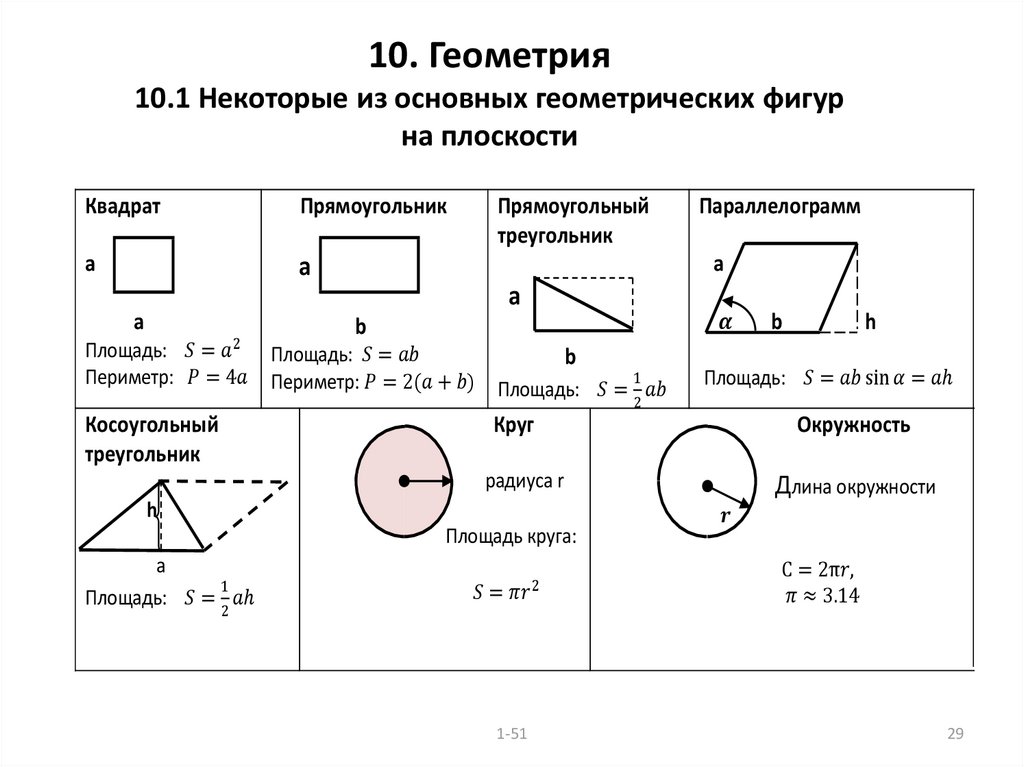
Тема 19. Геометрические фигуры на плоскости и их свойства
Содержание
Понятие геометрической фигуры.
Углы.
Параллельные и перпендикулярные прямые.
Треугольники.
Четырехугольники.
Многоугольники.
Окружность и круг.
Построение геометрических фигур на плоскости.
9. Преобразования геометрических фигур. Понятие преобразования
Основная литература 4, 5, 13, 14, 15, 28, 29, 34;
Дополнительная литература 13, 49, 51, 65, 68, 75, 76, 78, 85
1. Понятие геометрической фигуры
Геометрическую
фигуру определяют как любое множество точек.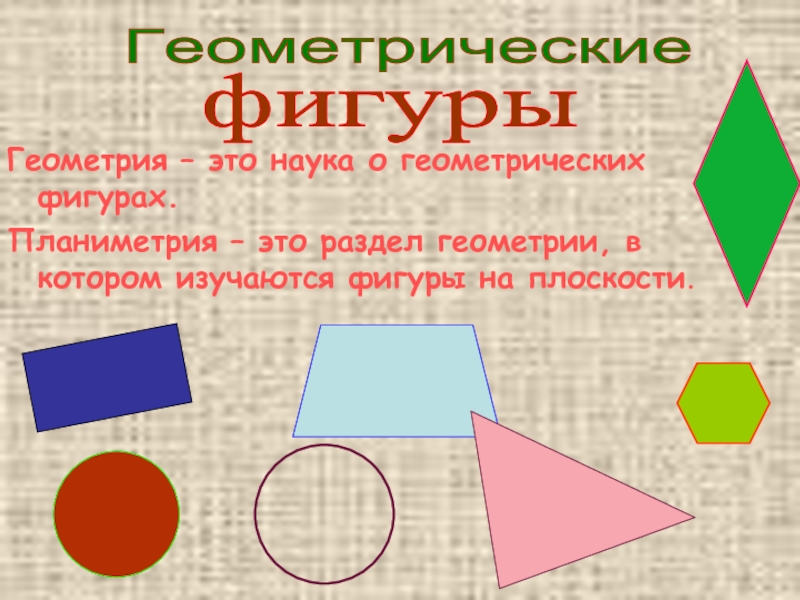
Отрезок, прямая, круг, шар — геометрические фигуры.
Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской.
Например, отрезок, прямоугольник — это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.
Так как понятие геометрической фигуры определено через понятие множества, то можно говорить о том, что одна фигура включена в другую (или содержится в другой), можно рассматривать объединение, пересечение и разность фигур.
Например, объединением двух лучей АВ и МК (рис. 1) является прямая КВ, а их пересечение есть отрезок АМ.
К А М В
Рис. 1
Различают выпуклые и невыпуклые фигуры.
Фигура
называется выпуклой,
если она вместе с любыми двумя своими
точками содержит также соединяющий их
отрезок.
Фигура F1, изображенная на рисунке 2, выпуклая, а фигура F2 — невыпуклая.
F2
X
Y
Выпуклыми фигурами являются плоскость, прямая, луч, отрезок, точка. Нетрудно убедиться в том, что выпуклой фигурой является круг (рис. 3). Если продолжить отрезокXY до пересечения с окружностью, то получим хорду АВ. Так как хорда содержится в круге, то отрезок XY тоже содержится в круге и, значит, круг — выпуклая фигура.
Для многоугольников известно другое определение: многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону.
Так
как равносильность этого определения
и данного выше для многоугольника
доказана, то можно пользоваться и тем,
и другим.
Основываясь на этих понятиях, рассмотрим другие геометрические фигуры, изучаемые в школьном курсе планиметрии. Рассмотрим их определения и основные свойства, принимая их без доказательства. Знание этого материала и умение применять к решению несложных геометрических задач является той основой, на которой можно строить методику обучения младших школьников элементам геометрии.
2. Углы
Напомним, что угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Лучи называются сторонами угла, а их общее начало — его вершиной.
Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и две точки на сторонах угла: А, (k,l), АВС.
Угол называется развернутым, если его стороны лежат на одной прямой.
Угол,
составляющий половину развернутого
угла, называется прямым.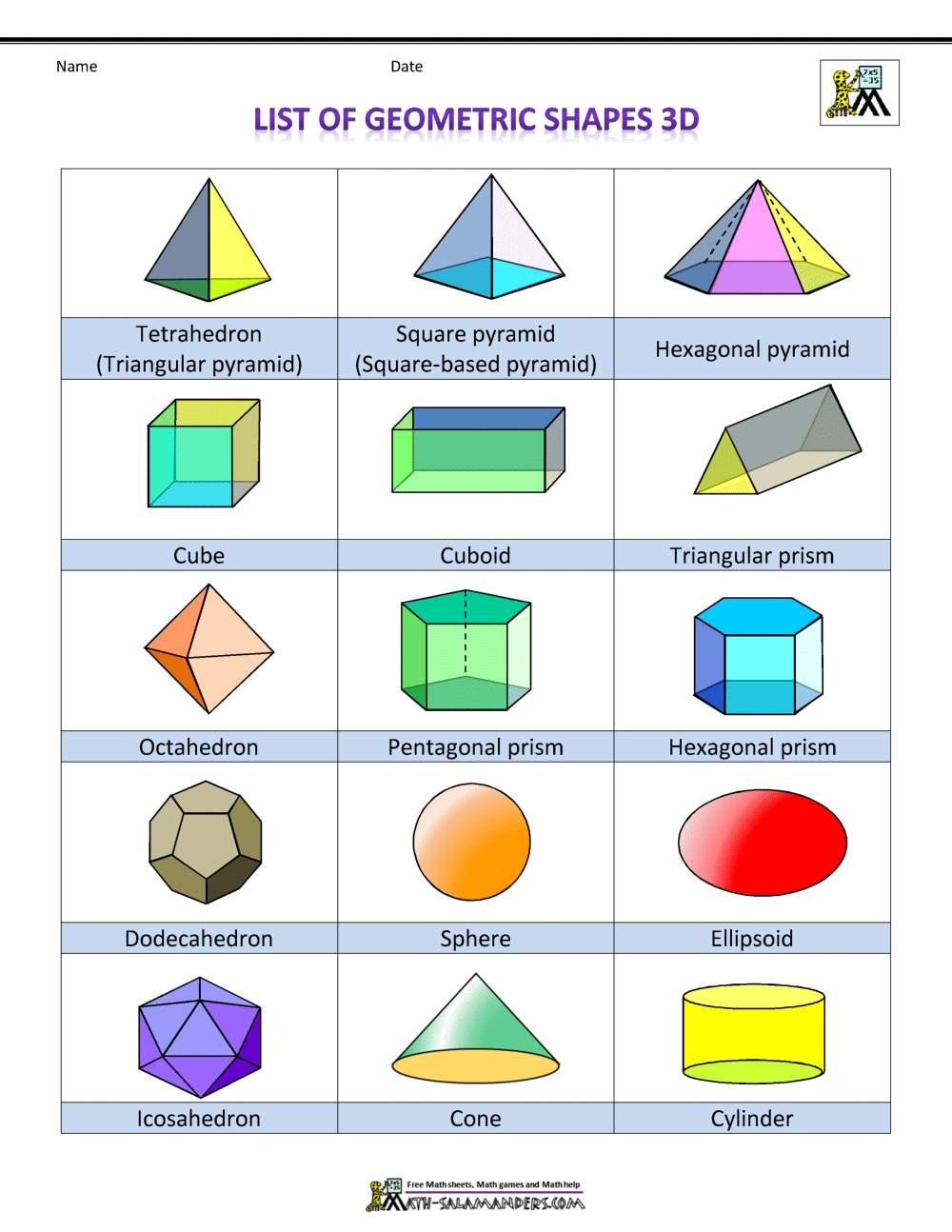 Угол, меньший прямого, называется острым. Угол, больший прямого, но меньший
развернутого, называется тупым.
Угол, меньший прямого, называется острым. Угол, больший прямого, но меньший
развернутого, называется тупым.
Кроме понятия угла, данного выше, в геометрии рассматривают понятие плоского угла.
Плоский угол — это часть плоскости, ограниченная двумя различными лучами, исходящими из одной точки.
Углы, которые рассматривают в планиметрии, не превосходят развернутого.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
Сумма смежных углов равна 180°. Справедливость этого свойства вытекает из определения смежных углов.
Два угла называютсявертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Углы АОВ и СОВ, а также углы АОС и D0В — вертикальные (рис. 4).
Вертикальные
углы равны.
Справедливость этого свойства вытекает из определения вертикальных углов и свойства смежных углов.
Плоские геометрические фигуры
Плоские геометрические фигуры
Пономарев П.В. 11МБОУ «Школа № 91 с углубленным изучением отдельных предметов»
Калина О.В. 11ФГБОУ ВО «Нижегородский государственный архитектурно-строительный университет»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия – одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.
Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.
В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий – понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии – теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).
На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества [1]. Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Объект исследования: Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.
Задачи исследования: Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.
Теоретическая и практическая значимость исследования состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.
Объем и структура исследования:
Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.
Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные геометрические фигуры в архитектуре зданий и сооружений
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии – планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.
Самой простой геометрической фигурой является точка. Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.
Прямая— одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой).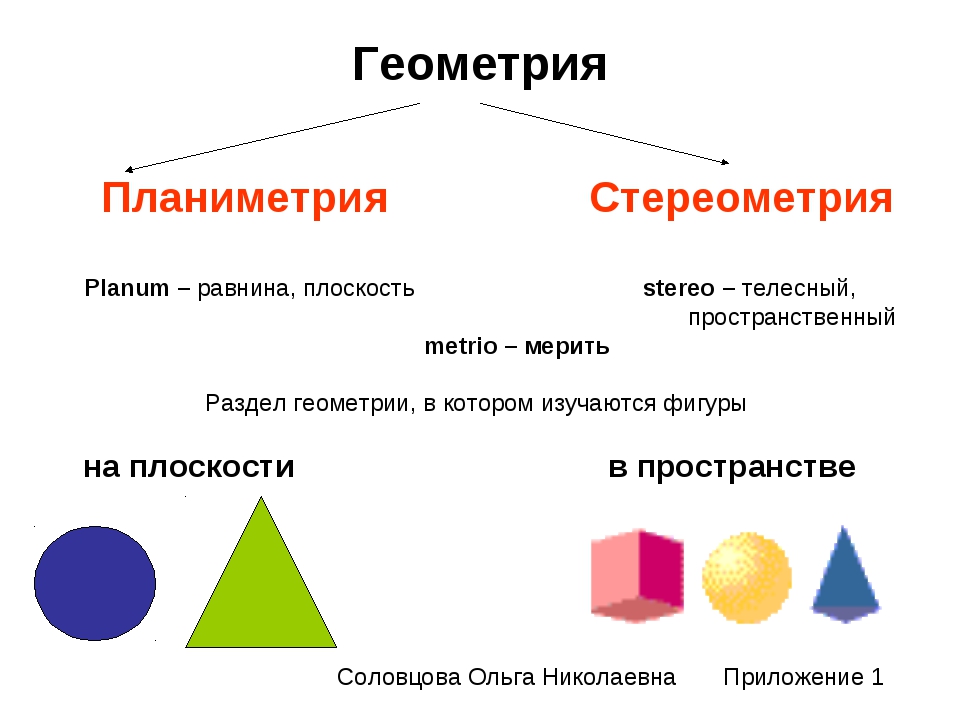 Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):
Прямые
Таблица 1
|
Параллельные прямые |
Свойства параллельных прямых |
Примеры в архитектуре зданий и сооружений |
|
Если прямые параллельны, то их одноименные проекции параллельны: |
Ессентуки, здание грязелечебницы (фото автора) |
|
|
Пересекающиеся прямые |
Свойства пересекающихся прямых |
Примеры в архитектуре зданий и сооружений |
|
Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи: |
Здания «горы» на Тайване https://www. |
|
|
Скрещивающиеся прямые |
Свойства скрещивающихся прямых |
Примеры в архитектуре зданий и сооружений |
|
Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. , ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях. |
Робер, Гюбер – Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287 |
1. 2. Плоские геометрические фигуры. Свойства и определения
2. Плоские геометрические фигуры. Свойства и определения
Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.
Четырехугольники:
Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Трапеция— это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Треугольник — это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.
Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:
|
«Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения, лежат, на одной окружности». |
|
|
Рис. 1.Окружность девяти точек |
|
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.
|
Тем удивительнее было открытие, сделанное американским математиком Франком Морли. Он доказал, что если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника (1899). |
|
|
Рис. 2.Открытие Франка Морли |
Многоуго́льник — это геометрическая фигура, обычно определяемая как замкнутая ломаная.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.
Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.
Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.
Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».
И первой задачей, которую я нашел, была головоломка «Танграм».
Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» ( греч. — «буква»).
Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5, квадрат 6 и параллелограмм 7. Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.
Рис.3. Элементы игры «Танграм» и геометрические фигуры
Рис.4. Задания «Танграм»
Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.
Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.
Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).
Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.
Рис. 5. Приёмы разрезаний
На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.
Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части[1].
Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части[1].
Рис.6.Примеры задач на разрезание:
—— — воссозданный квадрат; — разрез ножницами;
— основная фигура
2.2.Равновеликие и равносоставленные фигуры
Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.
|
На рисунке 6 показано как разбить многоугольники на одинаковое число соответственно равных частей (равные части отмечены одинаковыми цифрами). Эти два многоугольника являются равносоставленными[2]. |
|
|
Рис.6. Равносоставленные многоугольники |
Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.
Отсюда вытекает следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.
На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).
А Б
Рис.7. Преобразование «греческого креста»
В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет[1].
Рис.8. Паркет, собранный из греческого креста
Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).
|
Зная формулу площади прямоугольника, находим, что площадь параллелограмма равна произведению длин его стороны и соответствующей высоты. |
|
|
Рис.9. Равносоставленные параллелограмм и прямоугольник |
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.
|
Еще одну интересную задачу на равносотавленный треугольник и параллелограмм, можно использовапть для вычисления площадей многоугольников, способ этот был известен еще Евклиду, который жил более 2000 лет назад. |
|
|
Рис.10. Равносоставленные треугольник и параллелограмм |
Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.
Из этого положения легко выводится формула площади треугольника.
Отметим, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены.
Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.
Заключение
В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.
Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.
В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».
Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.
Библиографический список
1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. – Нижний Новгород: Изд-во НГТУ, 2002. – 73 с.
2. Энциклопедический словарь юного математика /Сост. А.П.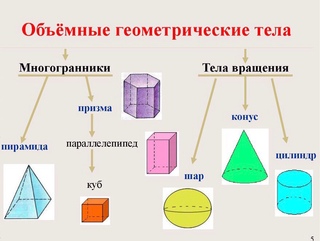 Савин. – М.: Педагогика, 1985. – 352 с.
Савин. – М.: Педагогика, 1985. – 352 с.
3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053
Приложение 1
Анкета-опросник для одноклассников
1. Знаете ли вы, что такое головоломка «Танграм»?
2. Что такое «греческий крест»?
3. Было бы вам интересно узнать, что такое «Танграм»?
4. Было бы вам интересно узнать, что такое «греческий крест»?
Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.
Приложение 2
Элементы игры «Танграм» и геометрические фигуры
Преобразование «греческого креста»
Просмотров работы: 5170
Геометрия в повседневной жизни | Статья в журнале «Юный ученый»
Геометрия — это раздел математики, который занимается изучением свойств геометрических фигур, что в переводе с латинского языка обозначает «внешний вид», «образ» [3]. Предмет исследования геометрии можно увидеть в жизни. Ведь эта наука возникла в Древнем Египте и развивалась в связи с потребностями практической деятельности человека: с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, при строительстве зданий и сооружений, прокладывании дорог. В древней архитектуре смело использовались самые разные геометрические формы. Египетские пирамиды имеют форму правильных четырехугольных пирамид.
Где бы мы не находились и чем бы мы не занимались, нас окружают предметы, имеющие форму геометрических фигур. При чем то, что имеет углы, отрезки и плоскости является объектом искусственного происхождения и изготовлено человеком. А предметы природного происхождения имеют округлые формы, такие как шар, окружность, дуга [1].
При чем то, что имеет углы, отрезки и плоскости является объектом искусственного происхождения и изготовлено человеком. А предметы природного происхождения имеют округлые формы, такие как шар, окружность, дуга [1].
Круг применяется и в искусстве, и в строительстве, и в технике. На дорогах и тротуарах не обходится без такой детали жилищно-коммунального хозяйства, как крышка канализационного люка. Ими закрывают отверстия, которые обеспечивают доступ в подземные коммуникации. У крышек канализационного люка целая история. Так, например, на первых изображали герб государства, агитационные лозунги. Сейчас на крышках отображают порядковый номер, дату и инициалы производителя. Но иногда встречаются разные теснение, узоры. Канализационная система в каждом государстве развивалась по-своему, но время появления первых канализационных люков практически везде сводится к середине XIX века. Поначалу их делали разной формы: и треугольной, и квадратной, и овальной. В последние годы изготавливают только модели круглой формы. [7]. И для этого есть целый ряд причин.
[7]. И для этого есть целый ряд причин.
Во-первых, это связано с экономией. Например, чтобы человек смог свободно проникнуть в колодец через квадратный люк, придется отверстие делать немного больше по площади. А значит, при изготовлении люка для такого отверстия пришлось затратить больше металла. В отличие от отверстия круглой формы, в которое легче всего пролезть человеку. Считается, что производство круглых люков на 40 % выгоднее по сравнению с производством квадратных.
Во-вторых, — безопасность. Круглая форма не дает люку провалиться вниз. Как бы ни пытались, не получится протолкнуть крышку в колодец. Чего нельзя сказать о квадратной форме люка: если квадратную крышку засунуть ребром по диагонали отверстия люка, она легко провалиться. Вследствие этого колодец останется открытый, и туда могут провалиться люди и животные, а также застрять машины.
В-третьих, — снова экономия. Круглая форма равномерно распределяет нагрузки при наезде на люк автомобиля. Следовательно, это позволяет немного уменьшить размер сечения (толщину), что в итоге способствует дополнительной экономии средств.
Следовательно, это позволяет немного уменьшить размер сечения (толщину), что в итоге способствует дополнительной экономии средств.
В-четвертых, — удобство. Чтобы быстро переместить крышку, круглый люк от колодца можно просто катить ребром. С этим справится даже один человек. А вот катить квадратный люк не получится — его придется либо перевозить, либо переносить вдвоем или даже втроем. Ведь люки изготовляют большей частью из чугуна.
И наконец, считается, что открывать круглую крышку канализационного люка проще из-за того, что любая точка ее окружности одновременно является точкой концентрации напряжения. У квадратных крышек всего две подобных точки — углы одной из сторон [4].
Отметим, что и сейчас не везде люки являются круглыми. В Индии часто встречаются треугольные формы. Квадратные формы используются в США и других странах Америки. В некоторых странах люки могут представлять собой вообще неопределенную геометрическую фигуру. Бывают с восемью углами и очень редко встречаются модели в форме ромба, полукругов.
Зато в строительстве всевозможных зданий человек преимущественно использует прямоугольные формы. Круглые помещения — это редкость и строятся из-за каких-либо функциональных особенностей таких зданий. В форме круга возводятся цирки, церкви, также стадионы могут быть округлой формы.
Археологи выяснили, что на самом деле первые жилища имели овальные формы. В некоторых регионах они сохранились и по сей день. И таких примеров было много. Вигвамы — у индейцев. Юрты — у тюркских и монгольских кочевников. Шатры — у восточных кочевых народов. Некоторые народности и сейчас строят круглое жилье. Эскимосы свои иглу строят из снега и льда в форме полусферы. Чукчи ставят чумы и яранги. У всех этих жилищ есть две общие черты. Во-первых, почти все их можно легко разобрать, перевезти и собрать на новом месте. Во-вторых, такие жилища строятся в пустынной местности. Это важно, чтобы аэродинамика шарообразных домов позволяла ветрам огибать их [5].
Трудно сказать, когда люди начали строить прямоугольные дома. Но в одном археологи и историки сходятся — это произошло, когда человек перешел к оседлому образу жизни. Ведь дома начали строить надолго. И, как оказалось, именно прямоугольная форма позволяет экономнее использовать пространство. Такие дома проще надстраивать и делить на комнаты. А значит, они дают максимальную площадь и экономическую выгоду. Но сегодня строители и архитекторы строительство домов прямоугольной формы считают небезопасным. Параллелепипеды (прямоугольники в объеме) относятся к плохо обтекаемым объектам. Когда ветер опоясывают здание, могут создаваться области, в которых воздушный поток закручивается. Высотные дома, которые стоят близко друг от друга, образуют впадины, в которых скорость ветра увеличивается вдвое. Заведующий лабораторией турбулентности минского Института тепло- и массообмена имени А. В. Лыкова Андрей Чорный объясняет: «С высотой скорость ветра очень быстро растет. Когда воздушная масса ударяется о здание, она как бы растекается в разные стороны, в том числе уходя вверх и вниз по стене. Спускающийся со здания поток попадает на улицу, а его скорость может даже превышать скорость набегающего потока, то есть „исходного“ ветра» [6].
Но при обтекании такого дома-параллелепипеда ветер отрывается с углов, а на боковых стенках и за жилищем слабеет. А на круглых домах, наоборот, поток на стенках ускоряется. Получается, что внутри него тепло, а на улице лютует ветер. Выход архитекторы нашли в строительстве зданий разной формы [2].
Но не только в строительстве и ЖКХ используются геометрические фигуры. В результате синтеза психологии и геометрии появилась новая наука. Психогеометрия позволяет прогнозировать и оценивать черты характера, модель поведения и стиль жизни человека с помощью простейших геометрических фигур. Молодая наука основывается на том, что разные геометрические формы вызывают у человека определённые эмоции. Так, овал и квадрат, быстрее всего регистрируется глазом и воспринимаются мозгом, а значит и лучше запоминаются, чем сложные и неправильные фигуры. Разработчик психогеометрии доктор психологии Сьюзен Деллингер из США. Она много лет проработала с персоналом и обобщила свой опыт. Созданный ей тест был назван в честь нее. Этот тест сейчас часто используется при приеме специалиста на работу. Претенденту на определенное место предлагается выбрать один из пяти фигур — квадрат, треугольник, прямоугольник, круг или зигзаг. Затем значение этих геометрических фигур соотносится с характером человека. И работодатель сразу определяет — подходит кандидат на данную вакансию или нет.
Этот же прием стали использовать при создании логотипов всевозможных компаний. При обозначении марок автомобилей конструкторы применяют круги, овалы, треугольники и зигзаги. Доказано, что формы линий влияют на скорость и качество восприятия информации: горизонтальные и вертикальные линии воспроизводят спокойствие и ясность, а изогнутые — изящество и непринуждённость.
В нашей жизни геометрия играет важную роль. Она нужна не только для того, чтобы назвать части строений или формы окружающего нас мира. С помощью геометрии мы можем решить многие задачи и ответить на разные вопросы. Геометрия дает не только представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, мыслить логически.
Математика всегда сопровождала человека в жизни. Она помогает развитию других наук. А также развивает у человека способность к творчеству и научной фантазии, находчивость и смекалку, а самое главное формирует логическое мышление: учит сравнивать, сопоставлять и классифицировать.
Литература:
- Депман И. и др. За страницами учебника математики 5–6 класс. / М.: Просвящение, 2004, — 287 с., ил.
- Журнал «Вокруг света» № 8 . /М: ООО «Издательство «Вокруг света», август 2017, -132 с.
- Прохоров Ю. В. — гл. ред. С. И. Адян и др. — Ред. кол. Математический энциклопедический словарь./ М.: Сов. Энциклопедия, 1988.- 847 с., ил.
- https://ashanet.ru/article/351887/pochemu-kanalizatsiya
- https://platinym.livejournal.com/3925283.html
- https://vsegda-tvoj.livejournal.com/30210436.html
- https://www.syl.ru/article/351887/pochemu-kanalizatsiya
— Простая английская Википедия, бесплатная энциклопедия
Группа фигурокПодвижный человек действия или фигурка — фигурка персонажа. Они могут быть сделаны из пластика или других материалов. Они часто основаны на персонажах из фильмов, комиксов, видеоигр или телепрограмм. Одна из самых известных фигурок — Г.И. Джо.
До 1960-х годов игрушки практически не двигались. Компания Hasbro в 1964 году представила новую игрушку, которую они назвали фигуркой .Эта игрушка была Г.И. Джо создан Стэном Уэстоном. Г.И. Джо выглядел в стиле милитари со сменной одеждой и аксессуарами, готовыми к действию. Фигурки были созданы, чтобы подарить мальчикам игрушки, так как Барби в 1959 году была так популярна среди девочек. Начиная с 1970-х годов супергерои комиксов превратились в фигурки боевиков. Marvel Comics и DC Comics начали делать свои фигурки, чтобы понравиться любимым детям супергероев.
Hasbro потратила много лет на сбор информации и чертежей военного оружия и транспортных средств для использования их боевых фигурок G.Джоуз И. Первый афроамериканец Г. Джо сделал на второй год фигурки. В 1967 году первая женщина G.I. Джо сделали, она была медсестрой. Г.И. Джо в 1985 году снялся в мультяшном телешоу, а в 2009 году был снят фильм.
На протяжении многих лет Hasbro создавала фигуры «людей действия», включая таких людей, как: Джордж Вашингтон, Роберт Э. Ли, Джон Ф. Кеннеди, Боб Хоуп и т. Д.
В 1980-х годах потребность в фигурках возросла со всеми мультфильмами, которые начали показывать на телевидении. Показывает, как Мастера Вселенной, Г.I. Joe и Thundercats, которые привлекли внимание маленьких мальчиков и дали потребность в фигурках их любимых шоу. Хасбро почерпнул идею Трансформеров, которые мы знаем сегодня, из мультфильма в Японии и привез его в Соединенные Штаты в 1984 году, вскоре появились эпизоды мультфильмов, а затем и фигурки.
К 1990-м годам фигурки стали игрушками и для взрослых, но их можно было собирать и ценить. Эти фигурки были взяты из фильмов, телевидения и известных людей, таких как рок-звезды.
С 2000-х годов и до наших дней произошел переход к фильмам, в которых в популярных фильмах были фигурки их собственных персонажей.И не только кино, но и музыканты, спортсмены и другие важные деятели СМИ.
Сегодня рынок коллекционеров фигурок для взрослых расширяется за счет таких компаний, как McFarlane Toys, Palisades и NECA. Компании предоставили многочисленным персонажам фильмов, музыкантам и спортсменам их самые первые детализированные фигурки. Они обычно предназначены для демонстрации, а не для игрушек; однако такие ориентированные на детей линии, как «Возрождение Мастеров Вселенной» и «Неограниченная Лига Справедливости», по-прежнему привлекают внимание взрослых коллекционеров.Комиксы также могут создавать фигурки своих персонажей, независимо от того, появлялись ли они в фильмах или мультфильмах. Примеры компаний, производящих комические фигурки и товары, включают почти исключительно Toy Biz и DC Direct.
Линии фигурок для взрослых часто предназначены только для определенных сетевых магазинов, а не для массовой розничной торговли. В популярных статьях часто есть цифры, доступные исключительно через почтовые предложения и комические соглашения, такие как comic con, что значительно повышает их ценность.Такие уловки, как «ошибки» упаковки и «короткие упаковки», также использовались компаниями по производству игрушек для повышения интереса коллекционеров.
Фигурки обычно изготавливаются из пластика. Эти игрушки способны двигаться и принимать разные позы. Создание фигурки начинается с идеи и рисунка. Далее изготавливаются модели из проволоки и глины. Когда фигура утверждается, ее лепят из пластика. Краска и ткань завершают игрушку.
- Базовая фигура действия: Начал с небольшого движения.Двигались бы только руки и, возможно, ноги.
- Подвижная фигурка: имеет больше областей движения, включая голову, запястья, колени, ступни, бедра, руки и ноги.
- Съемные / пристегивающиеся детали: Добавлена одежда, которую можно было снимать или надевать. Разные пушки и оружие. Даже лица разные.
- Звук: фигурки персонажей получили звуковые эффекты, такие как разговоры или звуки выстрелов.
- Военный
- Комические супергерои: Супермен, Бэтмен и т. Д.
- ТВ / фильм: He-Man, суперзвезды WWF / WWE, Властелин колец, Баффи Истребительница вампиров и т. Д.
- Известные люди: Поцелуй, президенты США, Джеки Чан, Рассел Кроу и т. Д.
- Женские фигурки: Женщина-кошка, Чудо-женщина, Сара Мишель Геллар и т. Д.
Фигурки были созданы, чтобы подарить мальчикам такую игрушку, как Барби. В отличие от Барби, Дж. Джо должен был быть мужественным и сильным, поэтому была создана военная игрушка.
Как и у Барби, тело фигурки показывает почти нереальный образ тела для мальчиков. У некоторых фигурок, таких как тело рестлера WWE на фигурке, есть нереальные мускулы.Эти изображения тел сильных борцов, супергероев и Г.И. Джо говорит мальчикам, что они тоже могут вырасти большими и сильными, что может быть не всегда.
Сегодня есть фигурки и для девочек. Фигурки героев кино, вроде Эдварда Каллена из фильма «Сумерки», собирают девушки.
- Игрушки и американская культура Шэрон М. Скотт
- История фигурок
- История фигурки
- Мужчины и фигурки: мужское тело
Фигурки из целлюлозы Home
Фигурки из целлюлозы для дома
Добро пожаловать на сайт Pulp Figures!
Являетесь ли вы закаленным ветераном дымящихся джунглей Борнео, известным исследователем, только что вернувшимся из ледяных пустошей высокой Арктики, солдатом удачи с мрачным лицом, привыкшим к захудалым переулкам Шанхая, или сваренным вкрутую шамусом со складками от пули. федора; вы нашли нужное место.
Некоторые кружки скажут тебе, что играть с игрушечными солдатиками — это для детей. После того, как вы сбили их с ног, возьмите свои кости и рукавицу, полную фигурок из целлюлозы, и присоединитесь к Rugged Adventure! .45s пылают, вы можете толкать этих заряженных персонажей по игровому столу; сражайтесь с безумными учеными, криминальными авторитетами или причудливыми лакеями, пока мама не позовет вас на ужин. Если снова это печень и лук, я бы порекомендовал притвориться, что вы не слышали, и вместо этого отправиться на поиски затерянного города.
Меня зовут Боб Марч, и я леплю эти мини-кружки, когда не читаю старые журналы и не гоняю собачьи упряжки здесь, в северных дебрях.Взгляните на мой сайт. Здесь найдется что-то для всех, кто живет с двумя руками!
Для оформления заказа по телефону:
Позвоните
250-317-7079
Я не всегда могу быть на связи, но я вам перезвоню.
_________________________________________________________________
Обратите внимание, что теперь адрес электронной почты Pulp Figures Snail Mail:
.Вопросы и комментарии присылайте по адресу:
[адрес электронной почты защищен]
Новый выпуск: набор для изготовления юнитов Mexican Federale # 1
Представляем PLT-11,
Ужасающий птеродактиль!
Напоминаем, что Pulp Alley выпустила набор блестящих карточек для всех персонажей Dangerous Dames.Вы можете получить их на сайте Pulp Alley:
https://store.pulpalley.com/category-s/1828.htm
В Crucible Crush мы собираем деньги для борьбы с коронавирусом Красного Креста. Вы можете помочь себе, купив ограниченный выпуск Black Sun Nurse Baker fig — кампанию, аналогичную ежегодной кампании Movember от Pulp Figure.
Новые опасные дамбы!
Last Year’s Limited Edition Fig от Marshal Grin Duster можно получить только в виде пожертвования на кампанию Movember за мужское здоровье.Щелкните здесь, чтобы узнать подробности:
В диапазоне Mystery & Horror Вещи стали более чудовищными:
Щелкните здесь, чтобы посетить кампанию Kickstarter.
игрушек WWE, фигурок Mattel WWE, фигурок Mattel Toy Wrestling
Войти | Зарегистрируйте свой аккаунт Товары В корзине 0 товаров Просмотр корзиныОформить заказ
Follow @RingsideC
- Товары
- Фигурки WWE — Mattel
- WWE Ringside WrestlingFigures.com Exclusives
- WWE Elite
- WWE Series
- WWE Battle Packs
- WWE Elite 2-Packs
- WWE Ultimate Edition
- WWE Retro Figures
- More WWE Mattel Figures
- Wicked Cool Toys
- New Japan Pro Wrestling ( NJPW)
- WWE Toy Wrestling Belts
- WWE Wrestling Rings & Playsets
- WWE Legends
- WWE Wrestling Buddies
- Women Superstars
- NXT
- Другие фигурки WWE
- Свободные фигурки и аксессуары
- Коллекция чемпионата WWE (1 16 статуй в масштабе)
- Фигурки AEW
- AEW Unrivaled
- AEW Ringside Exclusives
- AEW — Miscellaneous
- Ringside Exclusives
- Wrestling Figure Accessories
- WWE Ring
- WWE Ring Витрины
- Wh Игровые наборы eelchair
- Столы Ultimate
- Складные стулья
- Баррикады
- Игровые наборы с шкатулками
- Игровые наборы Ultimate с лестницей и столом
- Игровые наборы для комментаторов
- Ступеньки с кольцом
- Защитные чехлы «Figure Defender»
- Борцовские кольца и игровые наборы
- Реплика борцовских ремней
- Текущая копия рестлинговых ремней WWE
- Поиск по типу ремня
- Поврежденная упаковка
- UFC
- UFC Ultimate Series 9002
- Комплект принадлежностей UFC
- Посмотреть больше товаров
- Фигурки и аксессуары
- Другие игрушки
- Автографы
- Рекомендуемые товары
- Защитные рукава
- Фигурки WWE — Mattel
- Новые поступления
- Предварительный заказ ers
- Бестселлеры
- Магазин по имени
- Свяжитесь с нами
- Доставка
- О нас
.

 sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности.
Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности.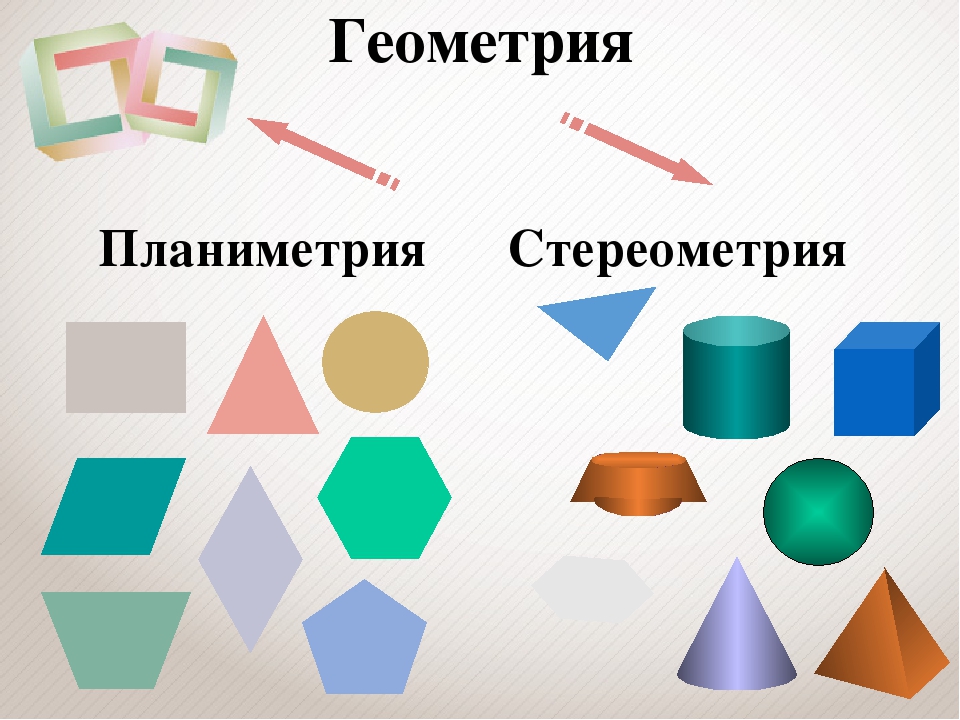

Leave a Comment