Чертеж куба: Чертеж куба. Обозначение куба на чертеже.
30.12.2021 


 Разное
Разное
Технический чертеж Волшебный куб План, куб, угол, прямоугольник, треугольник png
Технический чертеж Волшебный куб План, куб, угол, прямоугольник, треугольник pngтеги
- угол,
- прямоугольник,
- треугольник,
- симметрия,
- структура,
- lijnperspectief,
- квадрат,
- пространство Диагональ,
- трехмерное пространство,
- шейный куб,
- линия,
- рисунок,
- диаграмма,
- куб,
- круг,
- искусство,
- площадь,
- abcd,
- технический рисунок,
- магический куб,
- план,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 954x951px
- Размер файла
- 32.75KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
 93MB
93MB 16KB
16KB 57KB
57KB 34KB
34KB 26KB
26KB 24KB
24KB
 89KB
89KB 61KB
61KBВекторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространствеВыберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и :
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже.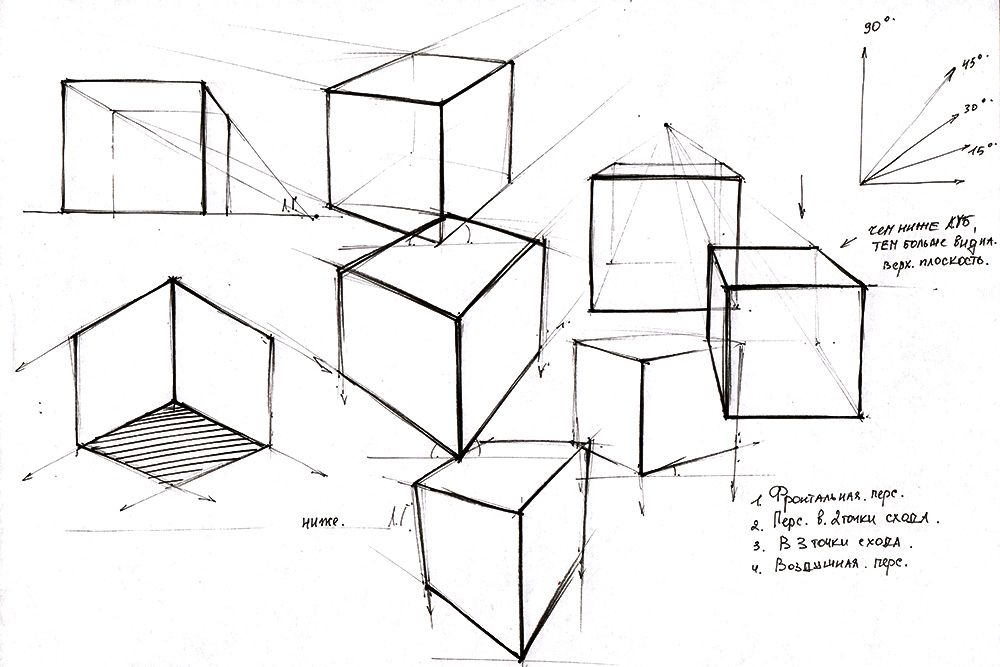 Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 07.02.2023
Как рисовать 3D-куб под разными углами — начинающий художник
Как рисовать
Byadmin
Хотите научиться рисовать трехмерные кубы? Тогда вы пришли в нужное место.
Преобразование объектов в их основные формы, такие как кубы и круги, как фундаментальный навык для художников.
Если вы умеете рисовать кубы в перспективе, вам будет намного легче научиться рисовать все остальное.
Итак, в этом уроке вы узнаете 3 разных способа рисования 3D-кубов.
Материалы
Поскольку мы просто делаем наброски, подойдет бумага для принтера или альбом для рисования. Если вы используете графитовые карандаши, предпочтительнее использовать более мягкие карандаши, такие как B, 2B или 3B. Это облегчит затенение. Однако подойдет любой карандаш, ручка или даже уголь.
Кроме того, вам могут быть полезны наши статьи о том, как рисовать прямые линии от руки и как разогреться перед рисованием.
Как нарисовать трехмерный куб
Метод 1
В этом первом методе вы нарисуете два квадрата, а затем соедините их края. Это самый простой метод из всех, но он ничему вас не научит относительно перспективы.
Шаг 1: нарисуйте квадрат
Начните с рисования квадрата нужного размера.
Шаг 2: нарисуйте второй квадрат
Затем нарисуйте второй квадрат того же размера, немного смещенный по горизонтали и вертикали.
Если вы нарисуете второй квадрат слишком далеко, вы получите прямоугольник вместо куба.
Шаг 3: соедините углы
Соедините верхний левый угол первого квадрата с нижним левым углом второго квадрата.
Повторите это для остальных трех углов, и вы нарисовали свой первый 3D-квадрат.
Метод 2
Во втором методе вы начнете с 2D-квадрата, а затем превратите его в 3D-куб.
Шаг 1: нарисуйте квадрат
Начните с рисования куба желаемого размера.
Шаг 2: расширение от углов
Теперь превратите свой 2D-куб в 3D-объект, расширив его в пространстве.
Вы делаете это, рисуя линии из каждого угла. Убедитесь, что каждая линия находится под одним и тем же углом.
Обратите внимание, что я не провел линию из нижнего левого угла. Это потому, что я хотел нарисовать цельный куб, и в этом случае вы не увидите эту грань.
Это потому, что я хотел нарисовать цельный куб, и в этом случае вы не увидите эту грань.
Однако при желании вы можете сделать пунктирную линию.
Шаг 3: соедините концы
Соедините все линии, чтобы завершить трехмерный куб.
Метод 3
Если вы действительно хотите научиться рисовать в перспективе, этот третий метод является лучшим. Это даст вам более фундаментальное понимание того, как рисовать вещи в 3D.
Шаг 1: нарисуйте вертикальную линию
Начните с рисования вертикальной линии. Поскольку мы нарисуем куб примерно под углом 45°, это будет край, ближайший к вам.
Шаг 2: начертите 4 направляющие
Нарисуйте направляющие, указывающие, куда пойдут стороны.
Вы хотите, чтобы верхние и нижние линии были параллельны друг другу.
Кроме того, вы хотите, чтобы левая и правая направляющие находились под углом 90° друг к другу.
Шаг 3: нарисуйте левый и правый край
Нарисуйте правый и левый края.
Если вы хотите нарисовать куб, попробуйте нарисовать оба куба на одинаковом расстоянии от центральной линии.
Если вы хотите нарисовать прямоугольник, вы можете поместить одну сторону дальше от центра, чем другую.
Шаг 4: соедините линии
Завершите рисование куба, соединив две стороны.
Обратите внимание, что эти две линии должны быть перпендикулярны направляющей, от которой они исходят.
Как нарисовать куб под разными углами
Теперь, когда вы знаете, как рисовать трехмерные кубы, почему бы вам не попробовать нарисовать кубы под разными углами?
Если вы освоили третий метод, это должно быть легко. Просто измените угол направляющих линий на шаге 2, чтобы нарисовать куб под любым углом.
Ниже вы можете увидеть, как я использовал этот метод для рисования кубов с 3-х разных углов.
Выход на новый уровень!
Кубики часто используются для упрощения более сложных форм. Тем не менее, кубы также могут быть центром ваших работ!
Например, вы можете совместить сегодняшний урок с предыдущей статьей о том, как нарисовать милые глазки маленькому семейству кубиков.
Или вы можете развить свою страсть к кубикам немного дальше и нарисовать полную картину о кубиках, как я сделал ниже. Я нарисовал это после того, как был вдохновлен удивительным искусством @XMIOart.
Похожие сообщения
Как рисовать
Verdigogh Zentangle | Как рисовать зентанглы
Bywytse
Многие цветочные композиции вдохновлены настоящими растениями, цветами и деревьями. И это также относится к Verdigogh! Если вы еще не заметили, Verdigogh вдохновлен веткой сосны. Этот клубок может показаться сложным на первый взгляд, но если вы знаете правильные шаги, его на самом деле на удивление легко нарисовать. Итак, давайте…
Подробнее Вердигог Зентангл | Как рисовать ZentanglesContinue
Как рисовать
Как рисовать свечу с пламенем
Byadmin
Хотите научиться рисовать свечу? Тогда вы пришли в нужное место! Если вы похожи на меня, то любите жечь свечи осенью, зимой, весной и летом. Независимо от времени и погоды. Итак, давайте научимся рисовать свечу и раскрашивать…
Подробнее Как нарисовать свечу с пламенемПродолжить
Как нарисовать куб в 3D
Узнайте, как нарисовать куб в 3D с помощью бесплатного пошагового руководства по рисованию, которое можно распечатать. Развлекайтесь простыми 3D-фигурами и развлекайтесь, как рисовать для детей всех возрастов.
Этот Как нарисовать куб в 3D для детей дарит нам всевозможные счастливые чувства. Это простой способ сделать набросок 3D-куба или коробки , используя только бумагу и карандаш.
Фигуры можно рисовать в любое время. Реальность такова, что учиться рисовать весело круглый год. Это учебник по рисованию кубов, который отлично подходит для детей всех возрастов.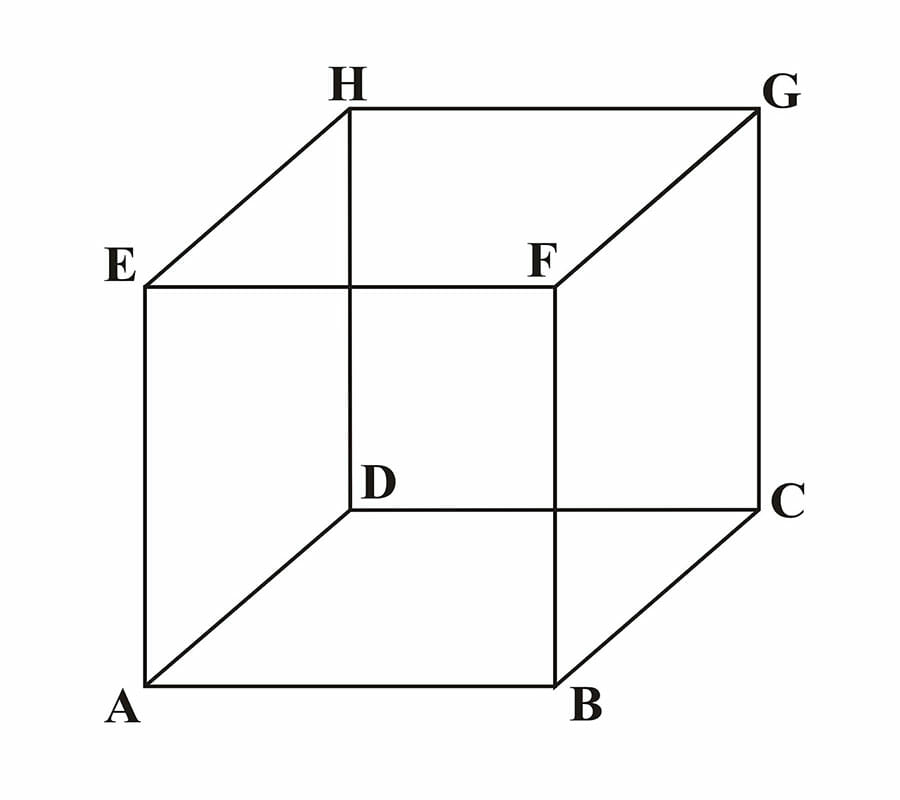
Что такое куб?
Прежде чем мы объясним куб, мы должны сначала определить квадратную форму. Квадрат представляет собой двумерную фигуру с четырьмя равными сторонами и четырьмя углами, каждый из которых имеет угол 90 градусов.
Куб, также известный как кубик, представляет собой прямоугольник или блок. Это более сложный объект (трехмерные объекты), чем квадрат, но все же одна из основных фигур рисования. В геометрии куб — это трехмерный объект с шестью различными квадратными гранями. Каждый с одинаковой длиной, шириной и высотой.
Куб имеет 6 сторон или граней одинаковой длины и 12 ребер. Каждый угол имеет прямой угол, равный 90 градусам. В этих уроках по кубам мы будем ссылаться на разные грани куба. Передняя и задняя грани, правая и левая боковые грани, верхняя и нижняя грани.
3D Cube Drawing Easy
Забавные простые руководства по рисованию, такие как этот 3D Cube Drawing, — отличный способ научиться рисовать. Учимся рисовать прямые линии, ничего сложного. Большинство линий представляют собой вертикальные линии (вверх и вниз) и горизонтальные линии (из стороны в сторону)
Большинство линий представляют собой вертикальные линии (вверх и вниз) и горизонтальные линии (из стороны в сторону)
Пока они не начнут это делать, они не осознают, насколько свободным может быть это и как легко создать что-то своими руками.
В рисовании куба есть что-то такое простое. Иметь под рукой этот забавный учебник для детей, чтобы научиться рисовать в любое время, — это все виды удовольствия и отличный способ изучить финансируемую геометрию.
Прежде чем вы начнете рисовать, мы также хотим убедиться, что у вас есть нужные инструменты. Вот бумага для рисования и карандаши для рисования, которые мы любим использовать.
Если вам нравится этот кубический рисунок, не пропустите наш комплект учебных пособий по рисованию животных, который включает 14 различных пошаговых руководств по рисованию, которые можно распечатать.
Как нарисовать коробку шаг за шагом
Ниже мы поделимся простым пошаговым уроком рисования с использованием прямых линий.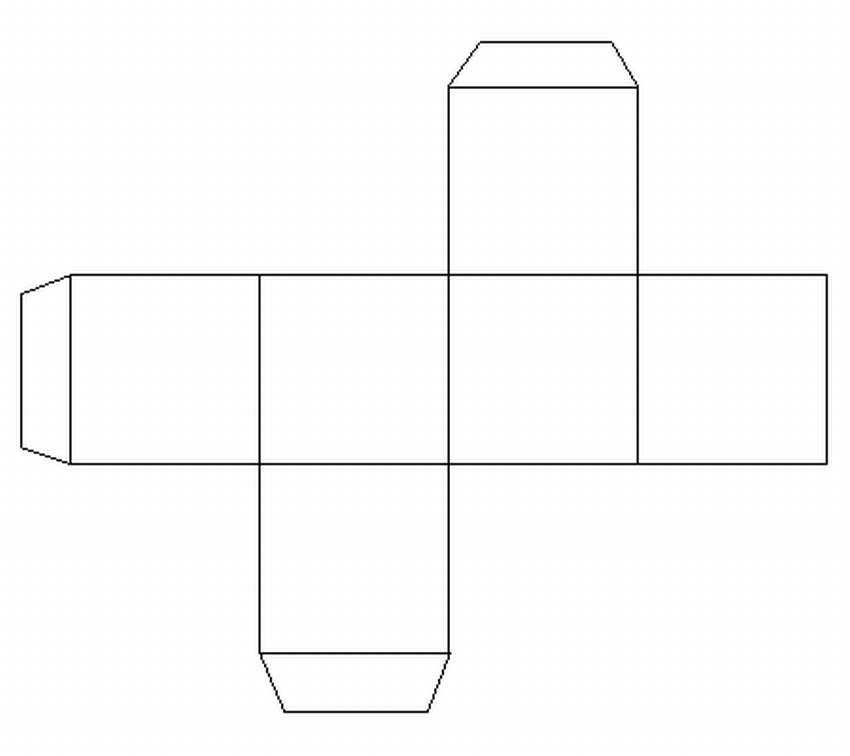 Не забудьте распечатать учебник по рисованию куба внизу и следуйте ему.
Не забудьте распечатать учебник по рисованию куба внизу и следуйте ему.
Следует отметить, что в этом уроке по кубу пунктирные линии представляют собой точку схода фигуры. Это означает, что вы можете нарисовать сплошную линию, но знайте, что эти линии в конечном итоге будут стерты, если вы рисуете сплошную форму. Лучше всего, чтобы линии карандаша были мягкими и их можно было стереть.
Возьмите лист бумаги, карандаш и линейку ( дополнительно ), если вы ищете прямой край при рисовании трехмерных кубов. Вот простые шаги, как нарисовать 3D-коробку.
3D-чертеж куба
Первый шаг — нарисовать квадрат. Нарисуйте прямую вертикальную линию справа, а затем слева. Затем две горизонтальные линии одинаковой длины.
Следующий шаг — нарисовать второй квадрат, обратную сторону куба, вверх и вправо. Эта левая сторона второго квадрата должна быть проведена через центр верхней части лицевого квадрата, а нижняя линия должна быть проведена через середину правой стороны лицевого квадрата.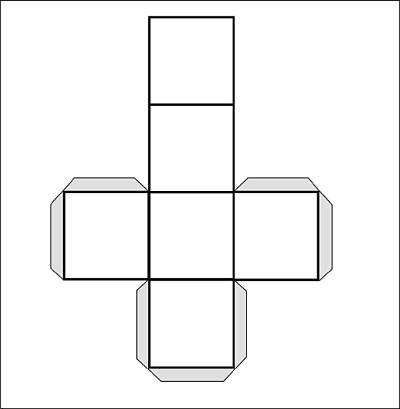
Следующий шаг — нарисовать правую грань куба. Это делается двумя диагональными линиями, проведенными из правого верхнего угла лицевой стороны в правый верхний угол задней грани. Далее следует провести линию, соединяющую правые нижние углы.
Последние две строки — это верхняя и нижняя линии левой боковой грани. Эти линии должны дать вам ромбовидные формы для верхней и нижней граней.
Рисование коробки
Последний шаг — стереть пунктирные линии нарисованного куба. Отсюда мне нравится проходить по нашим твердым карандашным линиям черным маркером. Если вы ищете больше трехмерного эффекта, то другой вариант — сделать пунктирные линии другого цвета, чем сплошные линии.
Раскрасьте свой кубик мелками, карандашами или фломастерами.
Мы выделили этот рисунок вместе с некоторыми другими забавными детскими поделками в майских поделках для Дня рисования в США вместе с нашими 101+ легкими поделками для детей.
Вы также не хотите пропустить наши 101+ раскраски для детей и 101+ печатные страницы для детей, полные поделок и раскрасок.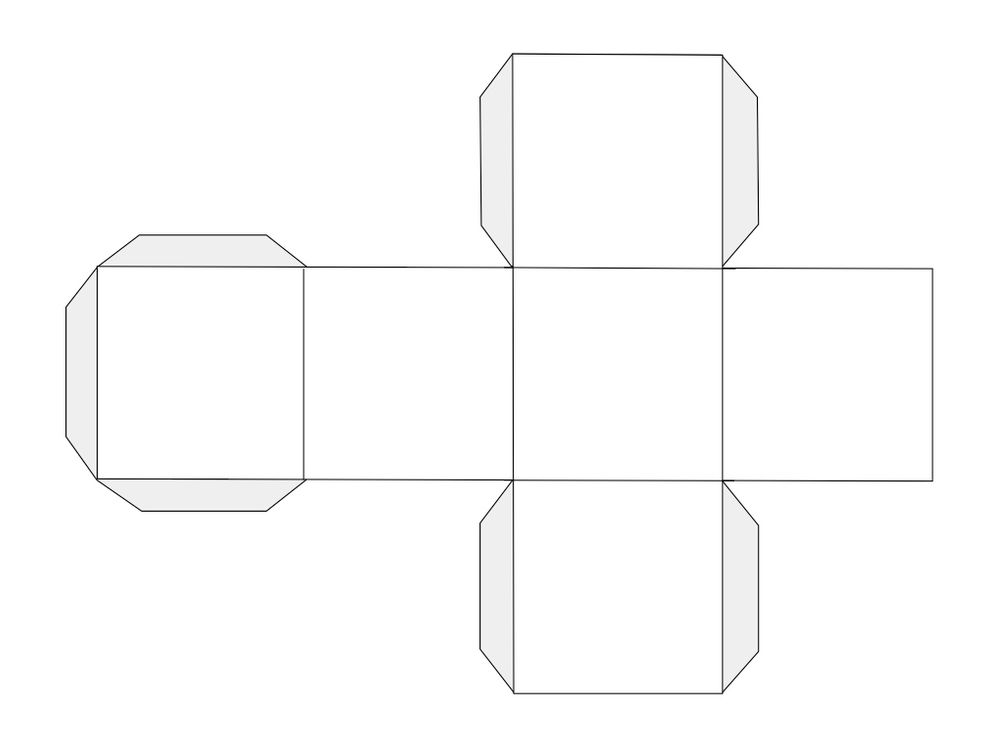

Leave a Comment